湘教版七年级数学下册期末复习课件 第4章 平行线与相交线常考题型讲解 (共32张PPT)
文档属性
| 名称 | 湘教版七年级数学下册期末复习课件 第4章 平行线与相交线常考题型讲解 (共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 405.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-08 08:02:47 | ||
图片预览

文档简介
(共32张PPT)
常考题型讲解
第四章--相交线与平行线
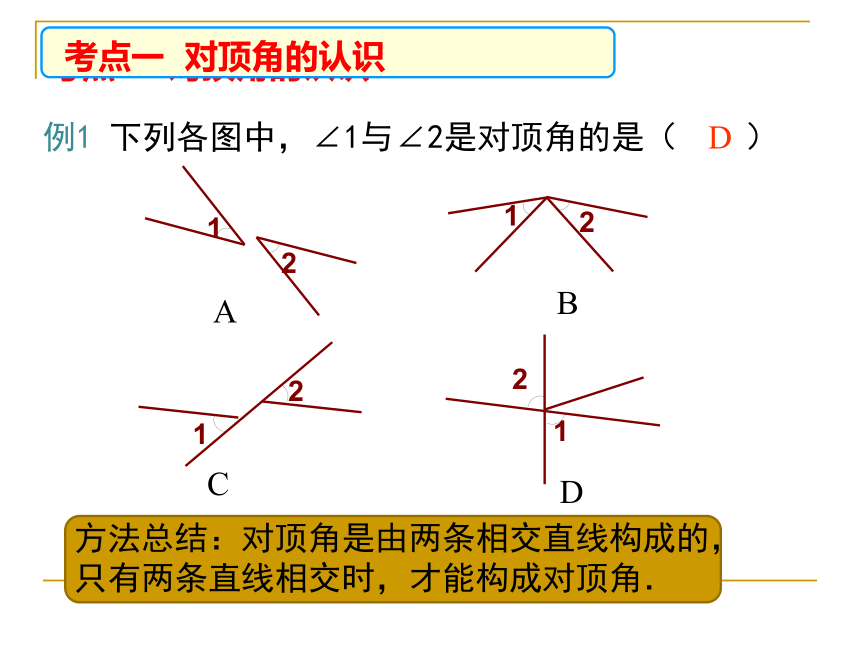
例1
下列各图中,∠1与∠2是对顶角的是(
)
1
2
C
1
2
D
D
1
2
A
1
2
B
方法总结:对顶角是由两条相交直线构成的,
只有两条直线相交时,才能构成对顶角.
考点一
对顶角的认识
考点一
对顶角的认识
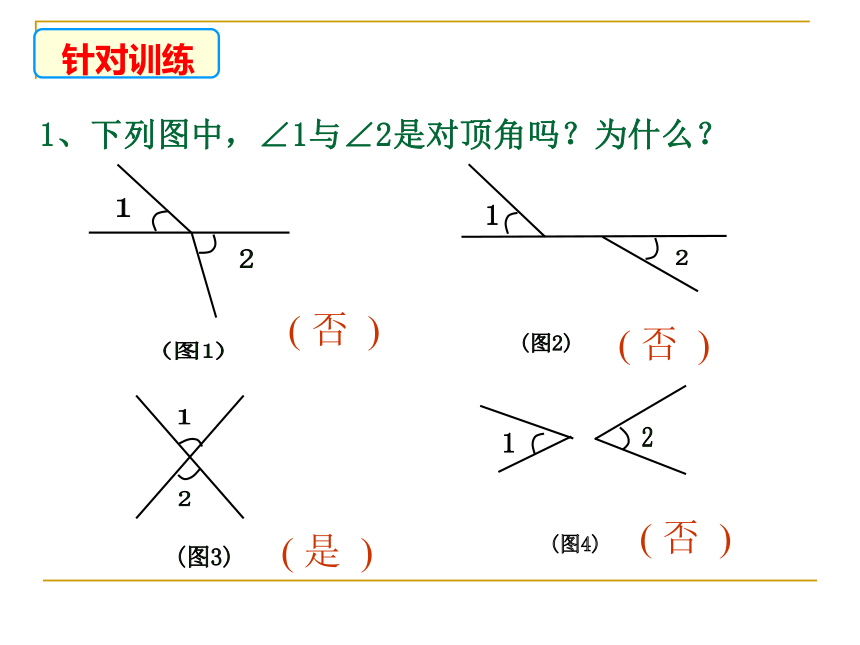
1、下列图中,∠1与∠2是对顶角吗?为什么?
(图1)
1
2
(图2)
(图3)
1
2
(图4)
1
2
1
2
(
否
)
(
否
)
(
否
)
(
是
)
针对训练
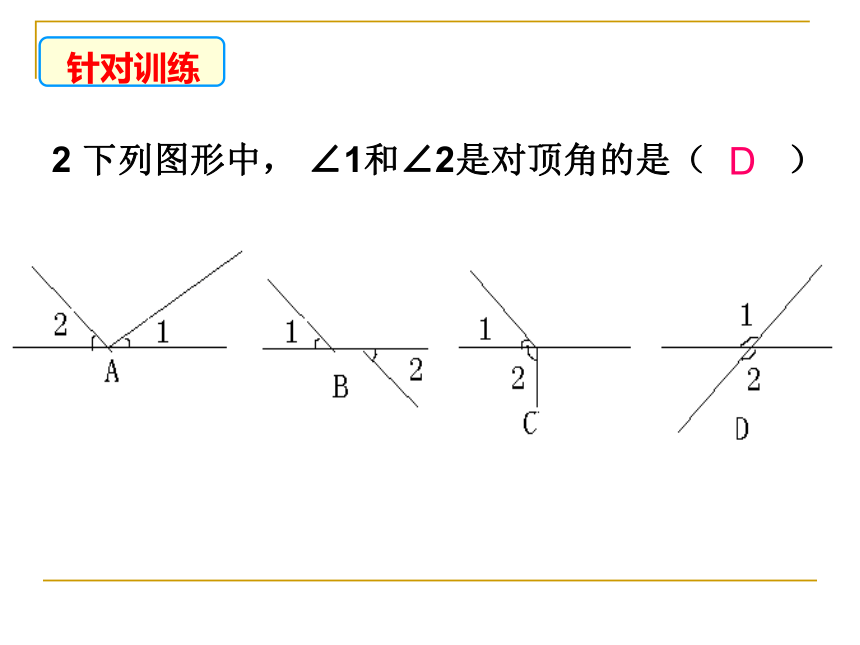
2
下列图形中,
∠1和∠2是对顶角的是(
)
D
针对训练
角的名称
角的特质
基本图形
基本图形
相同点
共同特征
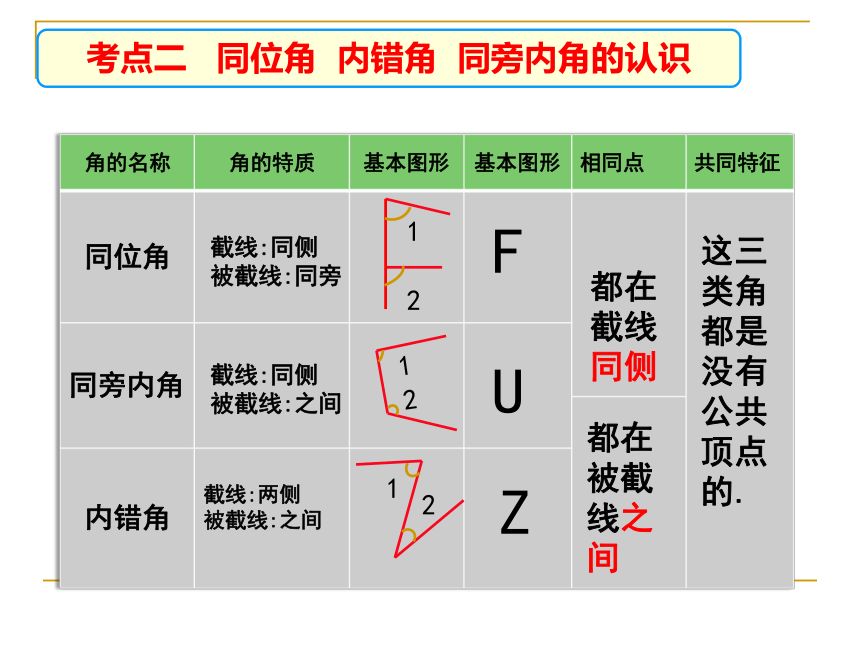
同位角
同旁内角
内错角
F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
1
2
1
2
1
2
都在截线同侧
都在被截线之间
这三类角都是没有公共顶点的.
考点二
同位角
内错角
同旁内角的认识
A
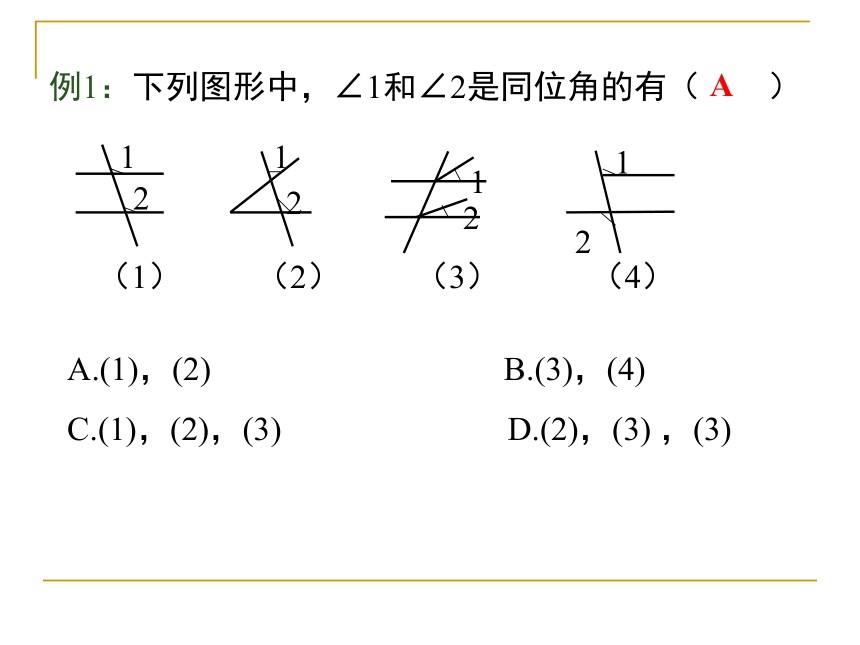
A.(1),(2)
B.(3),(4)
C.(1),(2),(3)
D.(2),(3)
,(3)
例1:下列图形中,∠1和∠2是同位角的有(
)
1
2
1
2
1
2
1
2
(1)
(2)
(3)
(4)
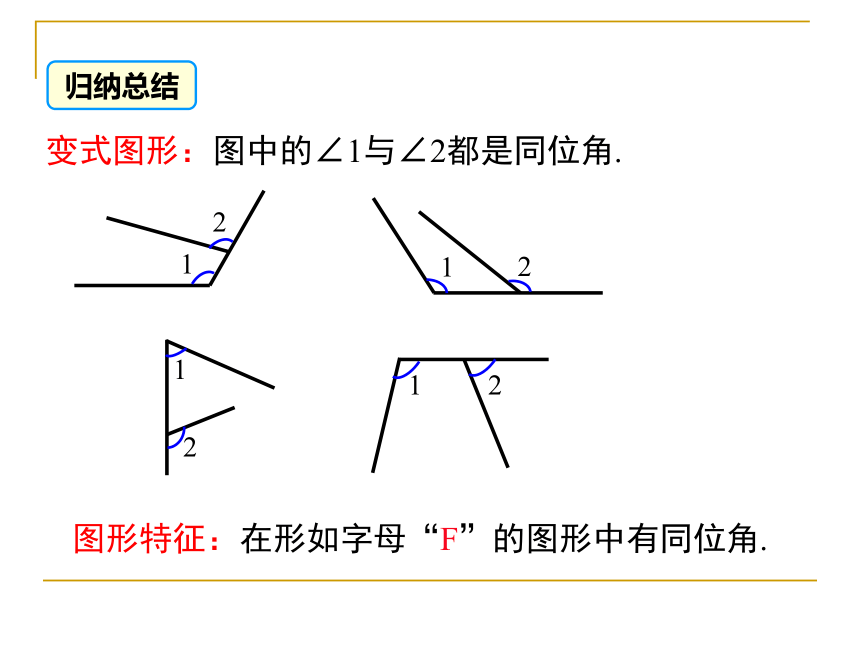
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1与∠2都是同位角.
1
2
1
2
1
2
1
2
归纳总结
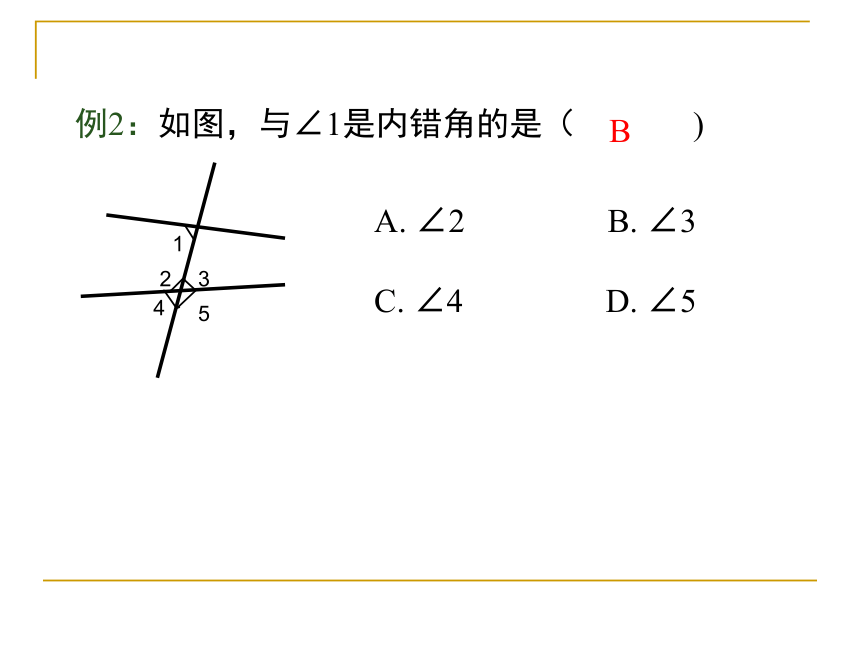
例2:如图,与∠1是内错角的是(
)
1
3
2
4
5
A.
∠2
B.
∠3
C.
∠4
D.
∠5
B
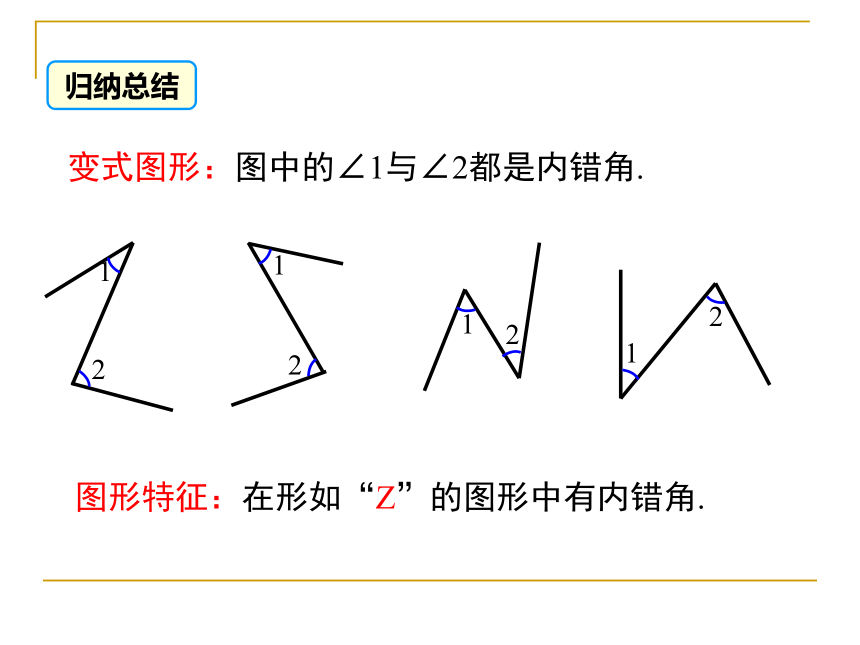
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
归纳总结
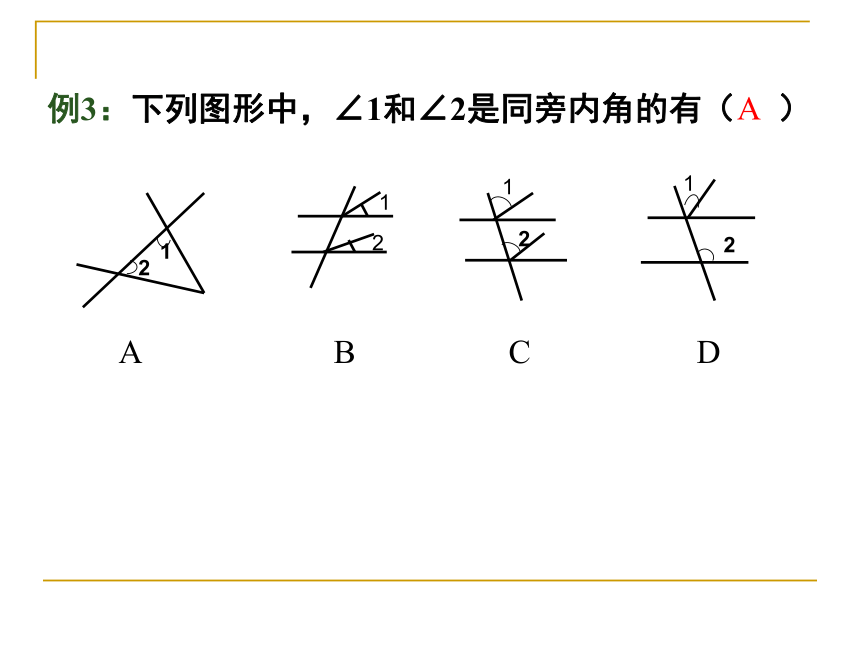
例3:下列图形中,∠1和∠2是同旁内角的有(
)
1
1
A
B
C
D
1
2
2
2
1
2
A
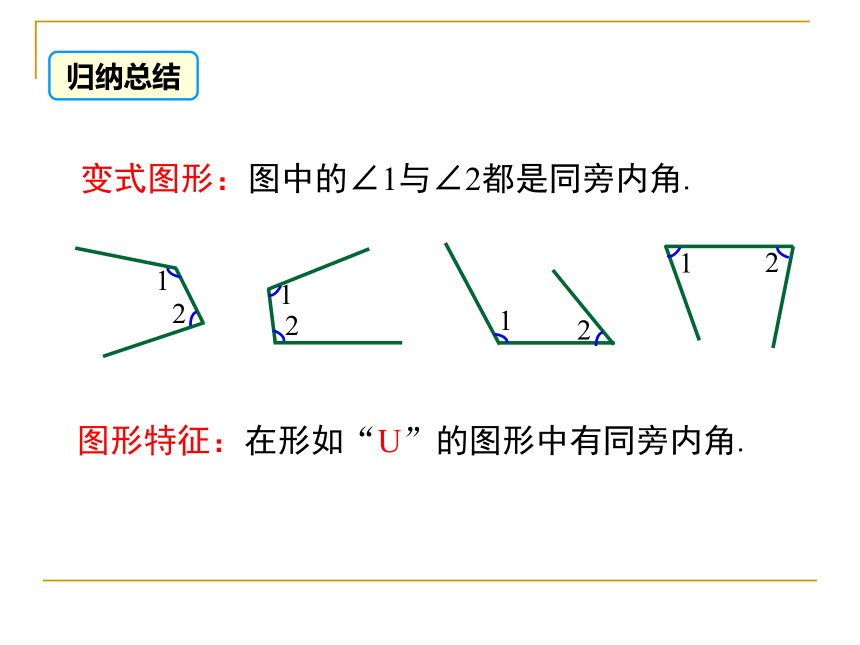
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
归纳总结
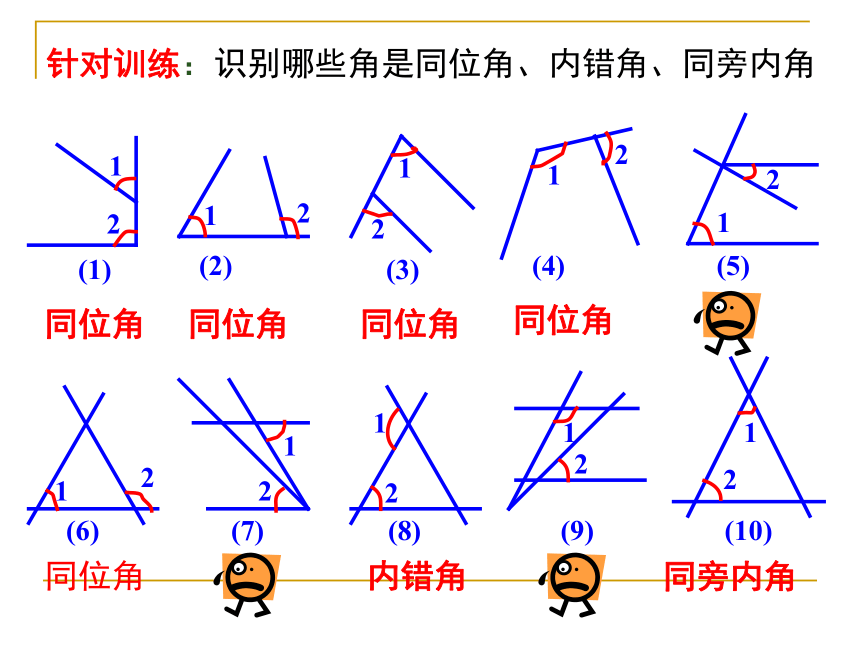
针对训练:识别哪些角是同位角、内错角、同旁内角
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
例1.下图中的变换属于平移的有哪些?
F
A
B
D
E
C
×
×
×
√
×
×
考点三
平移变换
1.平移改变的是图形的
(
)
A
、位置
B
、大小
C、
形状
D
、位置、大小和形状
2.经过平移,对应点所连的线段
(
)
A
、平行
B
、相等
C
、平行且相等
D、
既不平行,又不相等
A
C
针对训练
3.下面
2,3,4,5
幅图中哪幅图是由1平移得到的?
1
2
3
4
5
(1)
(2)
2
3
4
5
1
√
√
针对训练
考点四
利用对顶角、垂线的性质求角度
例1
如图,AB⊥CD于点O,直线EF过O点,∠AOE=65°,求∠DOF的度数.
B
A
C
D
F
E
O
解:
∵AB⊥CD,∴∠AOC=90°.
∵∠AOE=65°,
∴∠COE=25°.
又∵∠COE=∠DOF(对顶角相等),
∴∠DOF=25°.
1.如图.直线AB、CD相交于点O,OE⊥AB于O,OB平分∠
DOF,∠DOE=50°,求∠AOC、
∠
EOF、
∠
COF的度数.
解:∵AB⊥OE
(已知),
∴
∠EOB=90°(垂直的定义).
∵∠DOE=
50°
(已知),
∴
∠DOB=40°(互余的定义).
∴∠AOC=
∠DOB=40°(对顶角相等).
又∵OB平分∠DOF,
∴∠BOF=
∠DOB=40°(角平分线定义).
∴∠EOF=
∠EOB+
∠BOF=90°+40°=130°.
∴∠COF=∠COD-∠DOF=180°-80°=100°.
针对训练
考点五
点到直线的距离
例1
如图AC⊥BC,CD⊥AB于点D,CD=4.8cm,AC=6cm,
BC=8cm,则点C到AB的距离是
cm;点A到BC的距
离是
cm;点B到AC的距离是
cm.
4.8
6
8
例2
如图,设a,b,c是三条互相平行的直线.已知a与b的距离为5厘米,b与c的距离为2厘米,求a与c的距离.
在a上任其一点A,过A作AC⊥a,分别与b,c相交于B,C两点则AB,BC,AC分别表示a与b,b与c,a与c的公垂线段.
AC=AB+BC=5+2=7.
A
b
c
B
C
a
5厘米
2厘米
解:
因此a与c的距离是7厘米.
1.下列说法正确的是(
)
A.线段AB叫做点B到直线AC的距离
B.线段AB的长度叫作点A到直线AC的距离
C.线段BD的长度叫作点D到直线BC的距离
D.线段BD的长度叫作点B到直线AC的距离
A
B
C
D
D
针对训练
(1)如图1,
∵AB=5cm,
BC=2cm,
∴AC=7cm
A
B
C
针对训练:2
设a、b、c是三条互相平行的直线,已知a与b的距离为5cm,b与c
的距离为2cm,求a与c的距离.
解:有两种情况
图1
a
b
c
a
c
b
A
B
C
图2
(2)如图2
,
∵AB=5cm,
BC=2cm,
∴AC=3cm.
考点六
平行线的性质和判定
例1
(1)如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数;
解:∵∠1=∠2=72°,
∴a//b
(内错角相等,两直线平行).
∴∠3+∠4=180°
(两直线平行,同旁内角互补).
∵∠3=60°,∴∠4=120°.
a
b
1
.如图⑴,已知
AB∥CD,
∠1=30°,
∠2=90°,则∠3=___
2.
如图⑵,若AE∥CD,
∠EBF=135°,∠BFD=60°,
∠D=
(
)
A.75°
B.45°
C.30°
D.15°
图(1)
图(2)
60°
D
针对训练
解:
∵∠DAC=
∠ACB
(已知),
∴
AD//BC(内错角相等,两直线平行).
∵
∠D+∠DFE=180°(已知),
∴
AD//EF(同旁内角互补,两直线平行).
∴
EF//BC(平行于同一条直线的两条直线互相平行).
3
已知∠DAC=
∠ACB,
∠D+∠DFE=180°,
试说明:EF//BC.
A
B
C
D
E
F
4、已知
EF⊥AB,CD⊥AB,∠EFB=∠GDC,求:∠AGD=∠ACB。
证明:
∵
EF⊥AB,CD⊥AB
(已知)
∴
AD∥BC(垂直于同一条直线的两条
直线互相平行)
∴
∠EFB=
∠DCB
(两直线平行,同位角相等)
∵
∠EFB=∠GDC
(已知)
∴
∠DCB=∠GDC
(等量代换)
∴
DG∥BC
(内错角相等,两直线平行)
∴
∠AGD=∠ACB
(两直线平行,同位角相等)
考点七
相交线中的方程思想
例1
如图所示,
交于点O,
∠1=∠2,
∠3:∠1=8:1,
求∠4的度数.
4
1
2
3
解:设∠1的度数为x°,则∠2的度数为x°,
则∠3的度数为8x°,根据题意可得
x°+x°+8x°=180°,解得x=18.
即∠1=∠2=18°,
而∠4=∠1+∠2(对顶角相等).
故∠4=36°.
1.如图所示,直线AB与CD相交于点O,
∠AOC:∠AOD=2:3,求∠BOD的度数.
A
B
C
D
O
答案:72°
针对训练
例1:如图,若AB//CD,你能确定∠B、∠D与∠BED
的大小关系吗?说说你的看法.
B
D
C
E
A
解:过点E
作EF//AB.
∴∠B=∠BEF.
∵AB//CD.
∴EF//CD.
∴∠D
=∠DEF.
∴∠B+∠D=∠BEF+∠DEF
=∠DEB.
即∠B+∠D=∠DEB.
F
考点八
平行线中辅助线思想
1
如图,AB//CD,探索∠B、∠D与∠DEB的大小关系
.
针对训练
解:过点E
作EF//AB.
∴∠B+∠BEF=180°.
∵AB//CD.
∴EF//CD.
∴∠D
+∠DEF=180°.
∴∠B+∠D+∠DEB
=∠B+∠D+∠BEF+∠DEF
=360°.
即∠B+∠D+∠DEB=360°.
F
归纳:如图所示,AB∥CD,则
:
C
A
B
D
E
A
C
D
B
E2
E1
当有一个拐点时:
∠A+∠E+∠C=
360°
当有两个拐点时:
∠A+∠
E1
+
∠
E2
+∠C
=
540°
当有三个拐点时:
∠A+∠
E1
+
∠
E2
+∠
E3
+∠C
=
720°
A
B
C
D
E1
E2
E3
…
A
B
C
D
E1
E2
En
当有n个拐点时:
∠A+∠
E1
+
∠
E2
+…+∠
En
+∠C
=
180°
(n+1)
若有n个拐点,你能找到规律吗?
变式:如图,若AB∥CD,
则:
A
B
C
D
E
当左边有两个角,右边有一个角时:
∠A+∠C=
∠E
当左边有两个角,右边有两个角时:
∠A+∠F=
∠E
+∠D
C
A
B
D
E
F
E1
C
A
B
D
E2
F1
当左边有三个角,右边有两个角时:∠A+∠
F1
+∠C
=
∠
E1
+∠
E2
常考题型讲解
第四章--相交线与平行线
例1
下列各图中,∠1与∠2是对顶角的是(
)
1
2
C
1
2
D
D
1
2
A
1
2
B
方法总结:对顶角是由两条相交直线构成的,
只有两条直线相交时,才能构成对顶角.
考点一
对顶角的认识
考点一
对顶角的认识
1、下列图中,∠1与∠2是对顶角吗?为什么?
(图1)
1
2
(图2)
(图3)
1
2
(图4)
1
2
1
2
(
否
)
(
否
)
(
否
)
(
是
)
针对训练
2
下列图形中,
∠1和∠2是对顶角的是(
)
D
针对训练
角的名称
角的特质
基本图形
基本图形
相同点
共同特征
同位角
同旁内角
内错角
F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
1
2
1
2
1
2
都在截线同侧
都在被截线之间
这三类角都是没有公共顶点的.
考点二
同位角
内错角
同旁内角的认识
A
A.(1),(2)
B.(3),(4)
C.(1),(2),(3)
D.(2),(3)
,(3)
例1:下列图形中,∠1和∠2是同位角的有(
)
1
2
1
2
1
2
1
2
(1)
(2)
(3)
(4)
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1与∠2都是同位角.
1
2
1
2
1
2
1
2
归纳总结
例2:如图,与∠1是内错角的是(
)
1
3
2
4
5
A.
∠2
B.
∠3
C.
∠4
D.
∠5
B
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
归纳总结
例3:下列图形中,∠1和∠2是同旁内角的有(
)
1
1
A
B
C
D
1
2
2
2
1
2
A
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
归纳总结
针对训练:识别哪些角是同位角、内错角、同旁内角
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
例1.下图中的变换属于平移的有哪些?
F
A
B
D
E
C
×
×
×
√
×
×
考点三
平移变换
1.平移改变的是图形的
(
)
A
、位置
B
、大小
C、
形状
D
、位置、大小和形状
2.经过平移,对应点所连的线段
(
)
A
、平行
B
、相等
C
、平行且相等
D、
既不平行,又不相等
A
C
针对训练
3.下面
2,3,4,5
幅图中哪幅图是由1平移得到的?
1
2
3
4
5
(1)
(2)
2
3
4
5
1
√
√
针对训练
考点四
利用对顶角、垂线的性质求角度
例1
如图,AB⊥CD于点O,直线EF过O点,∠AOE=65°,求∠DOF的度数.
B
A
C
D
F
E
O
解:
∵AB⊥CD,∴∠AOC=90°.
∵∠AOE=65°,
∴∠COE=25°.
又∵∠COE=∠DOF(对顶角相等),
∴∠DOF=25°.
1.如图.直线AB、CD相交于点O,OE⊥AB于O,OB平分∠
DOF,∠DOE=50°,求∠AOC、
∠
EOF、
∠
COF的度数.
解:∵AB⊥OE
(已知),
∴
∠EOB=90°(垂直的定义).
∵∠DOE=
50°
(已知),
∴
∠DOB=40°(互余的定义).
∴∠AOC=
∠DOB=40°(对顶角相等).
又∵OB平分∠DOF,
∴∠BOF=
∠DOB=40°(角平分线定义).
∴∠EOF=
∠EOB+
∠BOF=90°+40°=130°.
∴∠COF=∠COD-∠DOF=180°-80°=100°.
针对训练
考点五
点到直线的距离
例1
如图AC⊥BC,CD⊥AB于点D,CD=4.8cm,AC=6cm,
BC=8cm,则点C到AB的距离是
cm;点A到BC的距
离是
cm;点B到AC的距离是
cm.
4.8
6
8
例2
如图,设a,b,c是三条互相平行的直线.已知a与b的距离为5厘米,b与c的距离为2厘米,求a与c的距离.
在a上任其一点A,过A作AC⊥a,分别与b,c相交于B,C两点则AB,BC,AC分别表示a与b,b与c,a与c的公垂线段.
AC=AB+BC=5+2=7.
A
b
c
B
C
a
5厘米
2厘米
解:
因此a与c的距离是7厘米.
1.下列说法正确的是(
)
A.线段AB叫做点B到直线AC的距离
B.线段AB的长度叫作点A到直线AC的距离
C.线段BD的长度叫作点D到直线BC的距离
D.线段BD的长度叫作点B到直线AC的距离
A
B
C
D
D
针对训练
(1)如图1,
∵AB=5cm,
BC=2cm,
∴AC=7cm
A
B
C
针对训练:2
设a、b、c是三条互相平行的直线,已知a与b的距离为5cm,b与c
的距离为2cm,求a与c的距离.
解:有两种情况
图1
a
b
c
a
c
b
A
B
C
图2
(2)如图2
,
∵AB=5cm,
BC=2cm,
∴AC=3cm.
考点六
平行线的性质和判定
例1
(1)如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数;
解:∵∠1=∠2=72°,
∴a//b
(内错角相等,两直线平行).
∴∠3+∠4=180°
(两直线平行,同旁内角互补).
∵∠3=60°,∴∠4=120°.
a
b
1
.如图⑴,已知
AB∥CD,
∠1=30°,
∠2=90°,则∠3=___
2.
如图⑵,若AE∥CD,
∠EBF=135°,∠BFD=60°,
∠D=
(
)
A.75°
B.45°
C.30°
D.15°
图(1)
图(2)
60°
D
针对训练
解:
∵∠DAC=
∠ACB
(已知),
∴
AD//BC(内错角相等,两直线平行).
∵
∠D+∠DFE=180°(已知),
∴
AD//EF(同旁内角互补,两直线平行).
∴
EF//BC(平行于同一条直线的两条直线互相平行).
3
已知∠DAC=
∠ACB,
∠D+∠DFE=180°,
试说明:EF//BC.
A
B
C
D
E
F
4、已知
EF⊥AB,CD⊥AB,∠EFB=∠GDC,求:∠AGD=∠ACB。
证明:
∵
EF⊥AB,CD⊥AB
(已知)
∴
AD∥BC(垂直于同一条直线的两条
直线互相平行)
∴
∠EFB=
∠DCB
(两直线平行,同位角相等)
∵
∠EFB=∠GDC
(已知)
∴
∠DCB=∠GDC
(等量代换)
∴
DG∥BC
(内错角相等,两直线平行)
∴
∠AGD=∠ACB
(两直线平行,同位角相等)
考点七
相交线中的方程思想
例1
如图所示,
交于点O,
∠1=∠2,
∠3:∠1=8:1,
求∠4的度数.
4
1
2
3
解:设∠1的度数为x°,则∠2的度数为x°,
则∠3的度数为8x°,根据题意可得
x°+x°+8x°=180°,解得x=18.
即∠1=∠2=18°,
而∠4=∠1+∠2(对顶角相等).
故∠4=36°.
1.如图所示,直线AB与CD相交于点O,
∠AOC:∠AOD=2:3,求∠BOD的度数.
A
B
C
D
O
答案:72°
针对训练
例1:如图,若AB//CD,你能确定∠B、∠D与∠BED
的大小关系吗?说说你的看法.
B
D
C
E
A
解:过点E
作EF//AB.
∴∠B=∠BEF.
∵AB//CD.
∴EF//CD.
∴∠D
=∠DEF.
∴∠B+∠D=∠BEF+∠DEF
=∠DEB.
即∠B+∠D=∠DEB.
F
考点八
平行线中辅助线思想
1
如图,AB//CD,探索∠B、∠D与∠DEB的大小关系
.
针对训练
解:过点E
作EF//AB.
∴∠B+∠BEF=180°.
∵AB//CD.
∴EF//CD.
∴∠D
+∠DEF=180°.
∴∠B+∠D+∠DEB
=∠B+∠D+∠BEF+∠DEF
=360°.
即∠B+∠D+∠DEB=360°.
F
归纳:如图所示,AB∥CD,则
:
C
A
B
D
E
A
C
D
B
E2
E1
当有一个拐点时:
∠A+∠E+∠C=
360°
当有两个拐点时:
∠A+∠
E1
+
∠
E2
+∠C
=
540°
当有三个拐点时:
∠A+∠
E1
+
∠
E2
+∠
E3
+∠C
=
720°
A
B
C
D
E1
E2
E3
…
A
B
C
D
E1
E2
En
当有n个拐点时:
∠A+∠
E1
+
∠
E2
+…+∠
En
+∠C
=
180°
(n+1)
若有n个拐点,你能找到规律吗?
变式:如图,若AB∥CD,
则:
A
B
C
D
E
当左边有两个角,右边有一个角时:
∠A+∠C=
∠E
当左边有两个角,右边有两个角时:
∠A+∠F=
∠E
+∠D
C
A
B
D
E
F
E1
C
A
B
D
E2
F1
当左边有三个角,右边有两个角时:∠A+∠
F1
+∠C
=
∠
E1
+∠
E2
同课章节目录
