2020年秋人教版数学九年级下册期末复习:第二十八章锐角三角函数 课件(图片版共43张PPT)
文档属性
| 名称 | 2020年秋人教版数学九年级下册期末复习:第二十八章锐角三角函数 课件(图片版共43张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-08 10:53:29 | ||
图片预览









文档简介
(共43张PPT)
期末复习课件
锐角三角函数
本章知识梳理
1.
利用相似的直角三角形,探索并认识锐角三角函数(sinA,cosA,tanA),知道30°、45°、60°角的三角函数值.
2.
会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它对应的锐角.
3.
能用锐角三角函数解直角三角形,能用相关知识解决一些简单的实际问题.
考纲要求
知识梳理
锐角三角函数的定义及相关
计算
在直角三角形中,当锐角A的大小确定时,∠A的对边与斜边的比叫做∠A的正弦,记作sinA;
在直角三角形中,当锐角A的大小确定时,∠A的邻边与斜边的比叫做∠A的余弦,记作cosA;
在直角三角形中,当锐角A的大小确定时,∠A的对边与邻边的比叫做∠A的正切,记作tanA.
特殊角的三角函数值:
解直角三角形
由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
如图M28-1,在Rt△ABC中,∠C=90°,则①三边之间的关系:
解直角三角形
的应用
解直角三角形的应用问题的一般过程:
①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题);
②根据题目已知特点,选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.
易错点
本章易错点归总
一、由于特殊角的三角函数值较多,在记忆时,有的同学没有准确记清或记混特殊角的三角函数值,从而导致解题出错.
【例1】sin60°等于
(
)
A.
B.
C.
D.
易错提示:学生往往记错记混sin30°与sin60°,tan30°与tan60°,防止此类错误的方法:一是用数形结合的思想,二是掌握锐角三角函数的增减性.
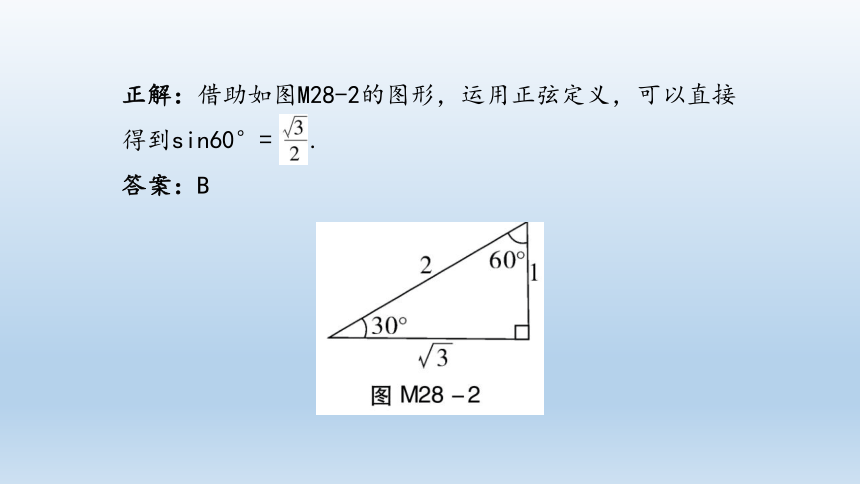
正解:借助如图M28-2的图形,运用正弦定义,可以直接得到sin60°=
.
答案:B
学以致用
1.在Rt△ABC中,∠C=90°,sinA=
,则∠A的度数是
( )
A.
30°
B.
45°
C.
60°
D.
90°
2.计算:tan45°sin45°-2sin30°cos45°.
A
易错点
二、用三角函数计算或在解直角三角形的应用题时,题目没有说明在直角三角形中,学生不去添加辅助线构造直角三角形,而粗心大意,片面地认为题目就是在直角三角形中,忽视了“在直角三角形”这个前提条件.
【例2】在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,且a:b:c=3:4:5,试证明:sinA+sinB=
.
易错提示:此题易错之处是没有说明∠C=90°,而直接将△ABC当做直角三角形,应用正、余弦函数的定义进行证明,容易得出如下错误:
学以致用
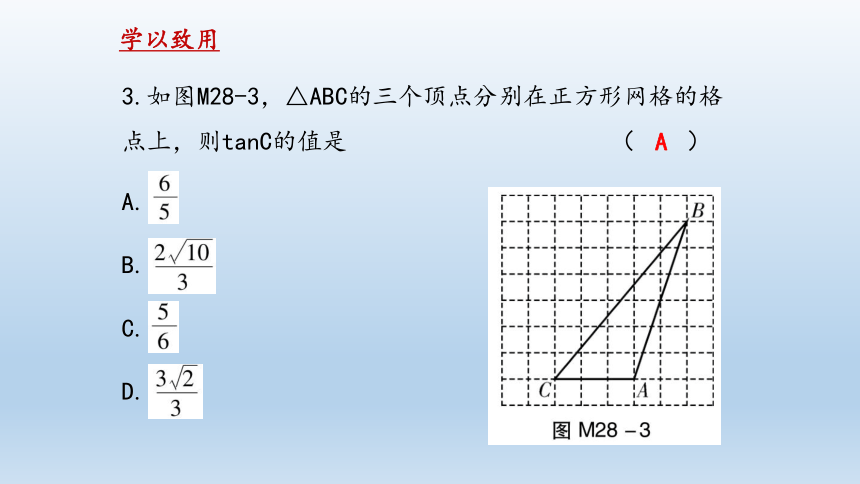
3.如图M28-3,△ABC的三个顶点分别在正方形网格的格点上,则tanC的值是
( )
A.
B.
C.
D.
A
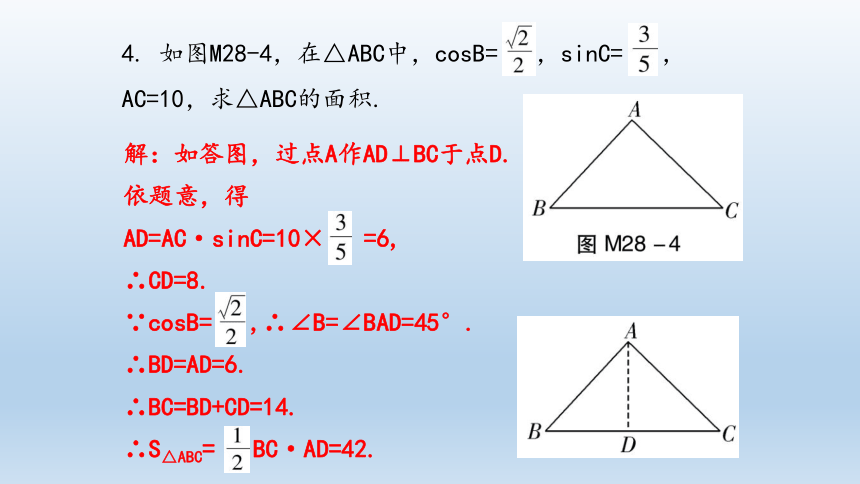
4.
如图M28-4,在△ABC中,cosB=
,sinC=
,AC=10,求△ABC的面积.
解:如答图,过点A作AD⊥BC于点D.
依题意,得
AD=AC·sinC=10×
=6,
∴CD=8.
∵cosB=
,∴∠B=∠BAD=45°.
∴BD=AD=6.
∴BC=BD+CD=14.
∴S△ABC=
BC·AD=42.
易错点
三、在题目没有给出图形时,容易忽略分类讨论,出现漏解情况,从而导致出错.
【例3】如果方程x2-4x+3=0的两个根分别是Rt△ABC的两条边长,Rt△ABC的最小角为∠A,那么tanA=__________.
易错提示:由方程x2-4x+3=0,解得x1=1,x2=3,至此,学生易粗心大意,立即得到tanA=
.
由于题目中既没有指明哪个角是直角,也没有指明哪条边是斜边,所以,应分类讨论,不能出现漏解的情况.
正解:由方程x2-4x+3=0,解得x1=1,x2=3.
①当3为直角边长时,tanA=
;
学以致用
5.已知在△ABC中,BC=6,AC=
,∠A=30°,则AB的长是__________.
6或12
一、锐角三角函数的定义
1.
在△ABC中,∠C=90°,则下列等式成立的是(
)
A.
B.
C.
D.
2.
在Rt△ABC中,∠C=90°,BC=1,AB=2,则∠A的余弦值等于
( )
A.
B.
C.
D.
考点1
锐角三角函数
B
A
3.
如图M28-5,△ABC的顶点都是正方形网格中的格点,
则tan∠ABC=_________.
4.
如图M28-6,△ABC的顶点是
正方形网格的格点,则tanA的值
为_________.
5.
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,a=2,b=1,求∠A的三个三角函数值.
6.
如图M28-7,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5,求∠A的三个三角函数值.
二、利用锐角三角函数求边长
7.
在Rt△ABC中,∠C=90°,∠A=α,AC=3,则AB的长可以表示为
( )
A.
B.
C.3sinα
D.
3cosα
A
8.
在Rt△ABC中,∠C=90°,AC=4,cosA的值等于
,则AB的长度是
(
)
A.
3
B.
4
C.
5
D.
9.
在Rt△ABC中,∠C=90°,若AB=4,sinA=
,则
斜边AB边上的高CD的长为__________.
10.
已知在Rt△ABC中,∠C=90°,AC=3,∠B=37°,则BC的长为_______.(提示:tan∠B=0.75,sin∠B=0.6,cos∠B=0.8)
D
4
11.
在△ABC中,∠C=90°,BC=24
cm,cosA=
,求这个三角形的周长.
解:可设AC=5x
cm,AB=13x
cm,则BC=12x
cm.
由12x=24,得x=2.
∴AB=26
cm,AC=10
cm.
∴△ABC的周长为10+24+26=60(cm).
12.
如图M28-8,在△ABC中,∠ACB=90°,sinA=
,BC=8,D是AB的中点,过点B作直线CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值.
一、特殊角的三角函数值
1.
sin30°的值为
( )
A.
B.
C.
D.
2.
计算:cos245°+sin245°=
( )
A.
B.
1
C.
D.
考点2
特殊角的三角函数值
D
B
3.
如图M28-9,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交
于点C,画射线OC,则sin∠AOC的值为__________.
4.
比较大小:sin30°_______sin45°.(填“>”“<”或“=”)
5.
计算:2cos230°-2sin60°×cos45°.
6.
计算:
.
<
解:原式=
.
解:原式=
-1.
二、利用特殊角的三角函数值求角度
7.
在△ABC中,∠A,∠B都是锐角,且cosA=
,sinB=
,则△ABC是
( )
A.
直角三角形
B.
钝角三角形
C.
锐角三角形
D.
不能确定
8.
已知∠C=75°,则∠A与∠B满足以下哪个选项才能构成△ABC?
( )
A.
B.
C.
D.
B
C
9.
若sinα=
,则锐角α=__________.
10.
若tan(α+10°)=
,则锐角α的度数是________.
11.
已知Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,3a=
b,求∠B的度数.
45°
50°
12.
如图M28-10,在锐角三角形ABC中,AB=6,AD是BC边上的高,BD=3,AC=
,求∠C的度数.
1.
在Rt△ABC中,∠C=90°,sinA=
,AC=6
cm,则BC的长度为
( )
A.
6
cm
B.
7
cm
C.
8
cm
D.
9
cm
2.
如图M28-11,以原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是
上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
( )
A.
(sinα,sinα)
B.
(cosα,cosα)
C.
(cosα,sinα)
D.
(sinα,cosα)
考点3
解直角三角形
C
C
3.
如图M28-12,Rt△ABC中,∠C=90°,BC=15,tanA=
,则AB=__________.
4.
如图M28-13,在Rt△ABC中,∠C=90°,AB=10,tanA=
,则AC的长是________.
17
8
5.
如图M28-14,在△ABC中,∠C=90°,∠ABC=60°.
若CD=2,AB=6,则S△ABD=_____________.
6.
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,a=3,b=
,解这个直角三角形.
解:∠A=30°,∠B=60°,c=6.
7.
如图M28-15,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.如果AC=
,且tan∠ACD=2,求AB的长.
解:在Rt△ABC中,
∵∠ACB=90°,CD⊥AB,
∴∠B=∠ACD.
∵tan∠ACD=2,∴tan∠B=
=2.
∴BC=
.
由勾股定理,得AB=5.
8.
如图M28-16,在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,且b=
,∠A的平分线AD=
,解这个直角三角形.
解:
依题意,得
cos∠CAD=
,
∴∠CAD=30°.
∵AD是∠CAB的平分线,
∴∠CAB=60°.
∴∠B=30°.
∴AB=2AC=
.
∴BC=
.
1.
如图M28-17,小华、小迪两家住在同一小区两栋相对的居民楼里,他们先测了两栋楼之间的距离BD为48
m,从小华家的窗户E处测得小迪家所住居民楼顶部C的仰角为30°,底部D的俯角为45°.
请你求
出小迪家所住居民楼的高度.
(结果
精确到1
m;参考数据:
≈1.4,
≈1.7)
考点4
解直角三角形的应用
解:由题意,得四边形EBDF为矩形,
∴EF=BD=48
m.
在Rt△ECF中,tan∠CEF=
,
∴CF=48×
=
(m).
在Rt△EFD中,∠FED=45°,
∴DF=EF=48
m.
∴CD=CF+FD=
+48≈75(m).
答:小迪家所住居民楼的高度约为75
m.
2.
如图M28-18,汽车在一条南北走向的公路上以每小时60
km的速度匀速向北行驶.
当汽车在A处时,某信号塔C在它的北偏西30°方向,汽车前行2
min,到达B处,此时信号塔C在它的北偏西45°方向.
(1)求AB的距离;
(2)求信号塔C到该公路的距离.
(
≈1.73,结果精确到0.1
km)
解;(1)AB=60×
=2(km).
(2)如答图M28-3,过点C作CD⊥AB于点D.
设CD=x,则在Rt△ACD和
Rt△BCD中,
∵∠CAD=30°,∠CBD=45°,
∴AD=
x,BD=x.
∵AB=AD-BD=2,
∴
x-x=2.
∴x=
≈2.7(km).
答:信号塔C到该公路的距离约为2.7
km.
3.
如图M28-19,四边形ABCD是某水库大坝的横截面示意图,坝高8
m,背水坡的坡角为45°,现需要对大坝进行加固,使上底加宽2
m,且加固后背水坡的坡度i=1∶2,求加固后坝底增加的宽度AF的长.
解:如答图M28-4,分别过点E,D作EG⊥AB,DH⊥AB交AB于点G,H.
∵四边形ABCD是梯形,且AB∥CD,
∴DH平行且等于EG.
∴四边形EGHD是矩形.∴ED=GH=2.
在Rt△ADH中,
,
在Rt△FGE中,
,
∴FG=2EG=16(m).
∴AF=FG+GH-AH=16+2-8=10(m).
答:加固后坝底增加的宽度AF的长是10
m.
4.
如图M28-20,一艘轮船在A处测得灯塔P在船的北偏东30°的方向,轮船沿着北偏东60°的方向航行16
km后到达B处,这时灯塔P在船的北偏西75°的方向.
求灯塔P与B之间的距离.(结果保留根号)
图M28-20
解:如答图M28-5,过点P作PH⊥AB于点H.
由题意,得∠PAB=30°,∠PBA=45°,
设PH=x,则AH=
x,BH=x,PB=
x.
∵AB=16,
∴
x+x=16.
解得x=
-8.
∴PB=
答:灯塔P与B之间的距离为
km.
谢谢
期末复习课件
锐角三角函数
本章知识梳理
1.
利用相似的直角三角形,探索并认识锐角三角函数(sinA,cosA,tanA),知道30°、45°、60°角的三角函数值.
2.
会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它对应的锐角.
3.
能用锐角三角函数解直角三角形,能用相关知识解决一些简单的实际问题.
考纲要求
知识梳理
锐角三角函数的定义及相关
计算
在直角三角形中,当锐角A的大小确定时,∠A的对边与斜边的比叫做∠A的正弦,记作sinA;
在直角三角形中,当锐角A的大小确定时,∠A的邻边与斜边的比叫做∠A的余弦,记作cosA;
在直角三角形中,当锐角A的大小确定时,∠A的对边与邻边的比叫做∠A的正切,记作tanA.
特殊角的三角函数值:
解直角三角形
由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
如图M28-1,在Rt△ABC中,∠C=90°,则①三边之间的关系:
解直角三角形
的应用
解直角三角形的应用问题的一般过程:
①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题);
②根据题目已知特点,选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.
易错点
本章易错点归总
一、由于特殊角的三角函数值较多,在记忆时,有的同学没有准确记清或记混特殊角的三角函数值,从而导致解题出错.
【例1】sin60°等于
(
)
A.
B.
C.
D.
易错提示:学生往往记错记混sin30°与sin60°,tan30°与tan60°,防止此类错误的方法:一是用数形结合的思想,二是掌握锐角三角函数的增减性.
正解:借助如图M28-2的图形,运用正弦定义,可以直接得到sin60°=
.
答案:B
学以致用
1.在Rt△ABC中,∠C=90°,sinA=
,则∠A的度数是
( )
A.
30°
B.
45°
C.
60°
D.
90°
2.计算:tan45°sin45°-2sin30°cos45°.
A
易错点
二、用三角函数计算或在解直角三角形的应用题时,题目没有说明在直角三角形中,学生不去添加辅助线构造直角三角形,而粗心大意,片面地认为题目就是在直角三角形中,忽视了“在直角三角形”这个前提条件.
【例2】在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,且a:b:c=3:4:5,试证明:sinA+sinB=
.
易错提示:此题易错之处是没有说明∠C=90°,而直接将△ABC当做直角三角形,应用正、余弦函数的定义进行证明,容易得出如下错误:
学以致用
3.如图M28-3,△ABC的三个顶点分别在正方形网格的格点上,则tanC的值是
( )
A.
B.
C.
D.
A
4.
如图M28-4,在△ABC中,cosB=
,sinC=
,AC=10,求△ABC的面积.
解:如答图,过点A作AD⊥BC于点D.
依题意,得
AD=AC·sinC=10×
=6,
∴CD=8.
∵cosB=
,∴∠B=∠BAD=45°.
∴BD=AD=6.
∴BC=BD+CD=14.
∴S△ABC=
BC·AD=42.
易错点
三、在题目没有给出图形时,容易忽略分类讨论,出现漏解情况,从而导致出错.
【例3】如果方程x2-4x+3=0的两个根分别是Rt△ABC的两条边长,Rt△ABC的最小角为∠A,那么tanA=__________.
易错提示:由方程x2-4x+3=0,解得x1=1,x2=3,至此,学生易粗心大意,立即得到tanA=
.
由于题目中既没有指明哪个角是直角,也没有指明哪条边是斜边,所以,应分类讨论,不能出现漏解的情况.
正解:由方程x2-4x+3=0,解得x1=1,x2=3.
①当3为直角边长时,tanA=
;
学以致用
5.已知在△ABC中,BC=6,AC=
,∠A=30°,则AB的长是__________.
6或12
一、锐角三角函数的定义
1.
在△ABC中,∠C=90°,则下列等式成立的是(
)
A.
B.
C.
D.
2.
在Rt△ABC中,∠C=90°,BC=1,AB=2,则∠A的余弦值等于
( )
A.
B.
C.
D.
考点1
锐角三角函数
B
A
3.
如图M28-5,△ABC的顶点都是正方形网格中的格点,
则tan∠ABC=_________.
4.
如图M28-6,△ABC的顶点是
正方形网格的格点,则tanA的值
为_________.
5.
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,a=2,b=1,求∠A的三个三角函数值.
6.
如图M28-7,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5,求∠A的三个三角函数值.
二、利用锐角三角函数求边长
7.
在Rt△ABC中,∠C=90°,∠A=α,AC=3,则AB的长可以表示为
( )
A.
B.
C.3sinα
D.
3cosα
A
8.
在Rt△ABC中,∠C=90°,AC=4,cosA的值等于
,则AB的长度是
(
)
A.
3
B.
4
C.
5
D.
9.
在Rt△ABC中,∠C=90°,若AB=4,sinA=
,则
斜边AB边上的高CD的长为__________.
10.
已知在Rt△ABC中,∠C=90°,AC=3,∠B=37°,则BC的长为_______.(提示:tan∠B=0.75,sin∠B=0.6,cos∠B=0.8)
D
4
11.
在△ABC中,∠C=90°,BC=24
cm,cosA=
,求这个三角形的周长.
解:可设AC=5x
cm,AB=13x
cm,则BC=12x
cm.
由12x=24,得x=2.
∴AB=26
cm,AC=10
cm.
∴△ABC的周长为10+24+26=60(cm).
12.
如图M28-8,在△ABC中,∠ACB=90°,sinA=
,BC=8,D是AB的中点,过点B作直线CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值.
一、特殊角的三角函数值
1.
sin30°的值为
( )
A.
B.
C.
D.
2.
计算:cos245°+sin245°=
( )
A.
B.
1
C.
D.
考点2
特殊角的三角函数值
D
B
3.
如图M28-9,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交
于点C,画射线OC,则sin∠AOC的值为__________.
4.
比较大小:sin30°_______sin45°.(填“>”“<”或“=”)
5.
计算:2cos230°-2sin60°×cos45°.
6.
计算:
.
<
解:原式=
.
解:原式=
-1.
二、利用特殊角的三角函数值求角度
7.
在△ABC中,∠A,∠B都是锐角,且cosA=
,sinB=
,则△ABC是
( )
A.
直角三角形
B.
钝角三角形
C.
锐角三角形
D.
不能确定
8.
已知∠C=75°,则∠A与∠B满足以下哪个选项才能构成△ABC?
( )
A.
B.
C.
D.
B
C
9.
若sinα=
,则锐角α=__________.
10.
若tan(α+10°)=
,则锐角α的度数是________.
11.
已知Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,3a=
b,求∠B的度数.
45°
50°
12.
如图M28-10,在锐角三角形ABC中,AB=6,AD是BC边上的高,BD=3,AC=
,求∠C的度数.
1.
在Rt△ABC中,∠C=90°,sinA=
,AC=6
cm,则BC的长度为
( )
A.
6
cm
B.
7
cm
C.
8
cm
D.
9
cm
2.
如图M28-11,以原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是
上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
( )
A.
(sinα,sinα)
B.
(cosα,cosα)
C.
(cosα,sinα)
D.
(sinα,cosα)
考点3
解直角三角形
C
C
3.
如图M28-12,Rt△ABC中,∠C=90°,BC=15,tanA=
,则AB=__________.
4.
如图M28-13,在Rt△ABC中,∠C=90°,AB=10,tanA=
,则AC的长是________.
17
8
5.
如图M28-14,在△ABC中,∠C=90°,∠ABC=60°.
若CD=2,AB=6,则S△ABD=_____________.
6.
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,a=3,b=
,解这个直角三角形.
解:∠A=30°,∠B=60°,c=6.
7.
如图M28-15,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.如果AC=
,且tan∠ACD=2,求AB的长.
解:在Rt△ABC中,
∵∠ACB=90°,CD⊥AB,
∴∠B=∠ACD.
∵tan∠ACD=2,∴tan∠B=
=2.
∴BC=
.
由勾股定理,得AB=5.
8.
如图M28-16,在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,且b=
,∠A的平分线AD=
,解这个直角三角形.
解:
依题意,得
cos∠CAD=
,
∴∠CAD=30°.
∵AD是∠CAB的平分线,
∴∠CAB=60°.
∴∠B=30°.
∴AB=2AC=
.
∴BC=
.
1.
如图M28-17,小华、小迪两家住在同一小区两栋相对的居民楼里,他们先测了两栋楼之间的距离BD为48
m,从小华家的窗户E处测得小迪家所住居民楼顶部C的仰角为30°,底部D的俯角为45°.
请你求
出小迪家所住居民楼的高度.
(结果
精确到1
m;参考数据:
≈1.4,
≈1.7)
考点4
解直角三角形的应用
解:由题意,得四边形EBDF为矩形,
∴EF=BD=48
m.
在Rt△ECF中,tan∠CEF=
,
∴CF=48×
=
(m).
在Rt△EFD中,∠FED=45°,
∴DF=EF=48
m.
∴CD=CF+FD=
+48≈75(m).
答:小迪家所住居民楼的高度约为75
m.
2.
如图M28-18,汽车在一条南北走向的公路上以每小时60
km的速度匀速向北行驶.
当汽车在A处时,某信号塔C在它的北偏西30°方向,汽车前行2
min,到达B处,此时信号塔C在它的北偏西45°方向.
(1)求AB的距离;
(2)求信号塔C到该公路的距离.
(
≈1.73,结果精确到0.1
km)
解;(1)AB=60×
=2(km).
(2)如答图M28-3,过点C作CD⊥AB于点D.
设CD=x,则在Rt△ACD和
Rt△BCD中,
∵∠CAD=30°,∠CBD=45°,
∴AD=
x,BD=x.
∵AB=AD-BD=2,
∴
x-x=2.
∴x=
≈2.7(km).
答:信号塔C到该公路的距离约为2.7
km.
3.
如图M28-19,四边形ABCD是某水库大坝的横截面示意图,坝高8
m,背水坡的坡角为45°,现需要对大坝进行加固,使上底加宽2
m,且加固后背水坡的坡度i=1∶2,求加固后坝底增加的宽度AF的长.
解:如答图M28-4,分别过点E,D作EG⊥AB,DH⊥AB交AB于点G,H.
∵四边形ABCD是梯形,且AB∥CD,
∴DH平行且等于EG.
∴四边形EGHD是矩形.∴ED=GH=2.
在Rt△ADH中,
,
在Rt△FGE中,
,
∴FG=2EG=16(m).
∴AF=FG+GH-AH=16+2-8=10(m).
答:加固后坝底增加的宽度AF的长是10
m.
4.
如图M28-20,一艘轮船在A处测得灯塔P在船的北偏东30°的方向,轮船沿着北偏东60°的方向航行16
km后到达B处,这时灯塔P在船的北偏西75°的方向.
求灯塔P与B之间的距离.(结果保留根号)
图M28-20
解:如答图M28-5,过点P作PH⊥AB于点H.
由题意,得∠PAB=30°,∠PBA=45°,
设PH=x,则AH=
x,BH=x,PB=
x.
∵AB=16,
∴
x+x=16.
解得x=
-8.
∴PB=
答:灯塔P与B之间的距离为
km.
谢谢
