盐城市初级中学苏科版八年级下册期末复习中心对称期末复习课件(共16张PPT)
文档属性
| 名称 | 盐城市初级中学苏科版八年级下册期末复习中心对称期末复习课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 587.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-08 08:04:55 | ||
图片预览



文档简介
(共16张PPT)
八年级(下册)
初中数学
期末复习(一)
中心对称图形
知识回顾:
知识点一、图形旋转与中心对称的概念
1.如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(-2,-2),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标
知识回顾:
【知识点二】中心对称的有关概念
2.在线段、角、平行四边形、长方形、圆、等边三角形中,是中心对称图形的有_____个,是轴对称图形的有_____个,既是中心对称图形又是轴对称图形的有______个.
知识回顾:
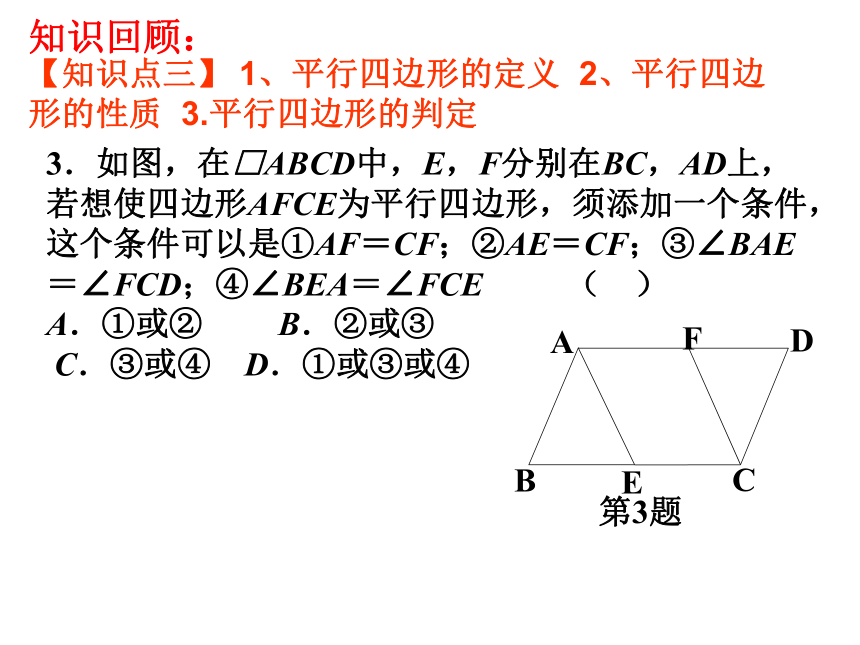
3.如图,在□ABCD中,E,F分别在BC,AD上,若想使四边形AFCE为平行四边形,须添加一个条件,这个条件可以是①AF=CF;②AE=CF;③∠BAE=∠FCD;④∠BEA=∠FCE
(
)
A.①或②
B.②或③
C.③或④
D.①或③或④
【知识点三】
1、平行四边形的定义
2、平行四边形的性质
3.平行四边形的判定
知识回顾:
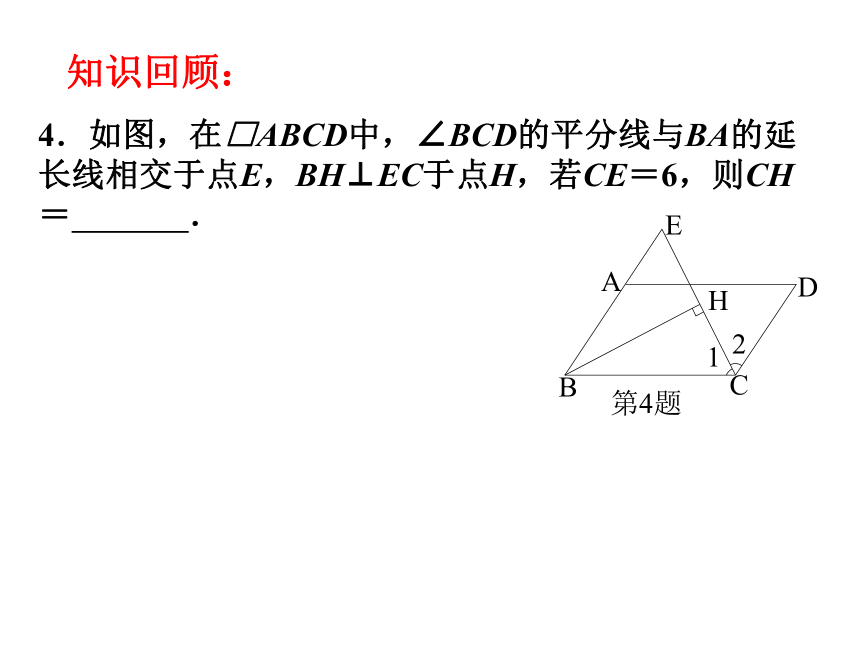
4.如图,在□ABCD中,∠BCD的平分线与BA的延长线相交于点E,BH⊥EC于点H,若CE=6,则CH=
.
知识回顾:
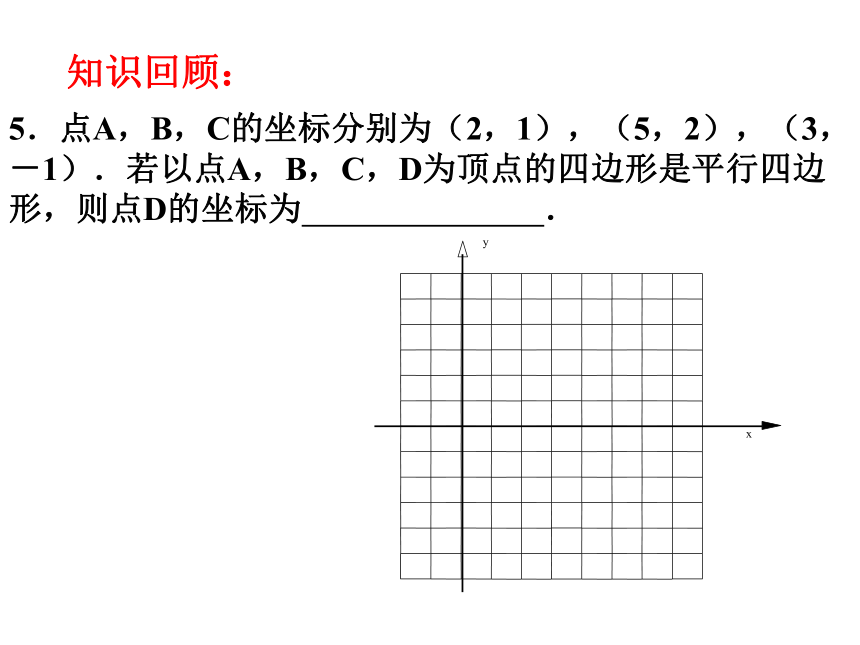
5.点A,B,C的坐标分别为(2,1),(5,2),(3,-1).若以点A,B,C,D为顶点的四边形是平行四边形,则点D的坐标为
.
【知识点四】矩形的性质与判定
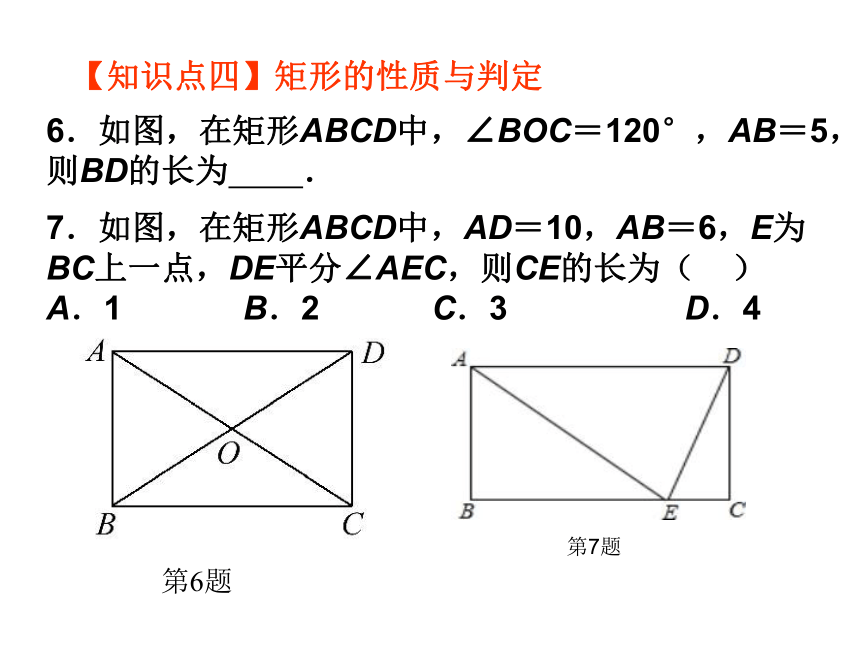
6.如图,在矩形ABCD中,∠BOC=120°,AB=5,则BD的长为
.
第6题
8.如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是
(
)
A.AB=BE
B.DE⊥DC
C.∠ADB=90°
D.CE⊥DE
第8题
【知识点五】菱形的性质与判定?
9.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.
若∠DAC=28°,则∠OBC的度数为
.
11.在矩形纸片ABCD中,AB=6,BC=8.
(2)将矩形纸片折叠,使点B与点D重合(如图②),求折痕GH的长.
(1)将矩形纸片沿BD折叠,点A落在E处(如图①),设DE与BC相交于点F,求BF的长;
12.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使□ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是
(
)
A.①②
B.②③
C.①③
D.②④
【知识点六】正方形的性质与判定?
13.如图,在正方形ABCD中,H是BC延长线上一点,使CE=CH,连接DH,延长BE交于DH于G,则下面结论错误的是(
)
A.BE=DH
B.
C
.
D.
【知识点六】正方形的性质与判定?
14.如图,E是边长为1的正方形ABCD的对角线BD上一点,
且BE=BC,P为CE上任意一点
于点Q,
于点R,则PQ+PR的值是
.
【知识点六】正方形的性质与判定
15.已知:E、F、G、H分别是四边形ABCD各边AB、BC、CD、DA的中点,
当四边形满足条件 时,四边形是菱形;
当四边形满足条件
时,四边形是矩形;
当四边形满足条件
时,四边形是正方形.
【知识点七】三角形的中位线
16.如图,在四边形ABCD中,对角线
,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点,若AC=10,BD=8,则四边形EFGH的面积为________.
【知识点七】三角形的中位线
【知识点七】三角形的中位线
八年级(下册)
初中数学
期末复习(一)
中心对称图形
知识回顾:
知识点一、图形旋转与中心对称的概念
1.如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(-2,-2),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标
知识回顾:
【知识点二】中心对称的有关概念
2.在线段、角、平行四边形、长方形、圆、等边三角形中,是中心对称图形的有_____个,是轴对称图形的有_____个,既是中心对称图形又是轴对称图形的有______个.
知识回顾:
3.如图,在□ABCD中,E,F分别在BC,AD上,若想使四边形AFCE为平行四边形,须添加一个条件,这个条件可以是①AF=CF;②AE=CF;③∠BAE=∠FCD;④∠BEA=∠FCE
(
)
A.①或②
B.②或③
C.③或④
D.①或③或④
【知识点三】
1、平行四边形的定义
2、平行四边形的性质
3.平行四边形的判定
知识回顾:
4.如图,在□ABCD中,∠BCD的平分线与BA的延长线相交于点E,BH⊥EC于点H,若CE=6,则CH=
.
知识回顾:
5.点A,B,C的坐标分别为(2,1),(5,2),(3,-1).若以点A,B,C,D为顶点的四边形是平行四边形,则点D的坐标为
.
【知识点四】矩形的性质与判定
6.如图,在矩形ABCD中,∠BOC=120°,AB=5,则BD的长为
.
第6题
8.如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是
(
)
A.AB=BE
B.DE⊥DC
C.∠ADB=90°
D.CE⊥DE
第8题
【知识点五】菱形的性质与判定?
9.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.
若∠DAC=28°,则∠OBC的度数为
.
11.在矩形纸片ABCD中,AB=6,BC=8.
(2)将矩形纸片折叠,使点B与点D重合(如图②),求折痕GH的长.
(1)将矩形纸片沿BD折叠,点A落在E处(如图①),设DE与BC相交于点F,求BF的长;
12.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使□ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是
(
)
A.①②
B.②③
C.①③
D.②④
【知识点六】正方形的性质与判定?
13.如图,在正方形ABCD中,H是BC延长线上一点,使CE=CH,连接DH,延长BE交于DH于G,则下面结论错误的是(
)
A.BE=DH
B.
C
.
D.
【知识点六】正方形的性质与判定?
14.如图,E是边长为1的正方形ABCD的对角线BD上一点,
且BE=BC,P为CE上任意一点
于点Q,
于点R,则PQ+PR的值是
.
【知识点六】正方形的性质与判定
15.已知:E、F、G、H分别是四边形ABCD各边AB、BC、CD、DA的中点,
当四边形满足条件 时,四边形是菱形;
当四边形满足条件
时,四边形是矩形;
当四边形满足条件
时,四边形是正方形.
【知识点七】三角形的中位线
16.如图,在四边形ABCD中,对角线
,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点,若AC=10,BD=8,则四边形EFGH的面积为________.
【知识点七】三角形的中位线
【知识点七】三角形的中位线
同课章节目录
