2020年春苏科版八年级数学下册期末培优复习第11章 反比例函数 (含答案)
文档属性
| 名称 | 2020年春苏科版八年级数学下册期末培优复习第11章 反比例函数 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 340.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-07 23:22:39 | ||
图片预览

文档简介
第11章
反比例函数
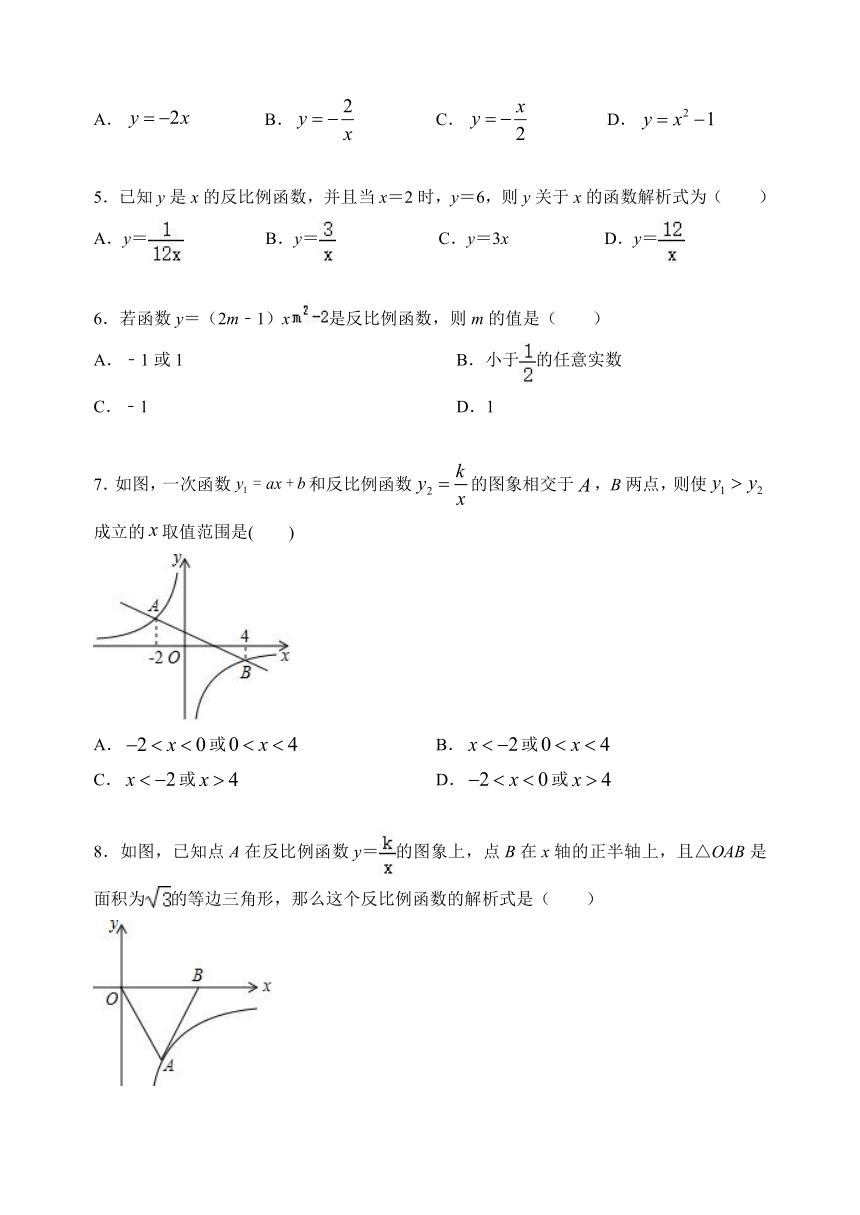
1.若双曲线y=在每一个象限内,y随x的增大而减小,则k的取值范围是( )
A.k≠3
B.k<3
C.k≥3
D.k>3
2.若ab>0,则一次函数y=ax﹣b与反比例函数y=在同一坐标系数中的大致图象是( )
A.
B.
C.
D.
3.如图,点的坐标是是等边三角形,点在第一象限.若反比例函数的图象经过点,则的值是(
)
A.
B.
C.
D.
4.下列函数是反比例函数的是(
)
A.
B.
C.
D.
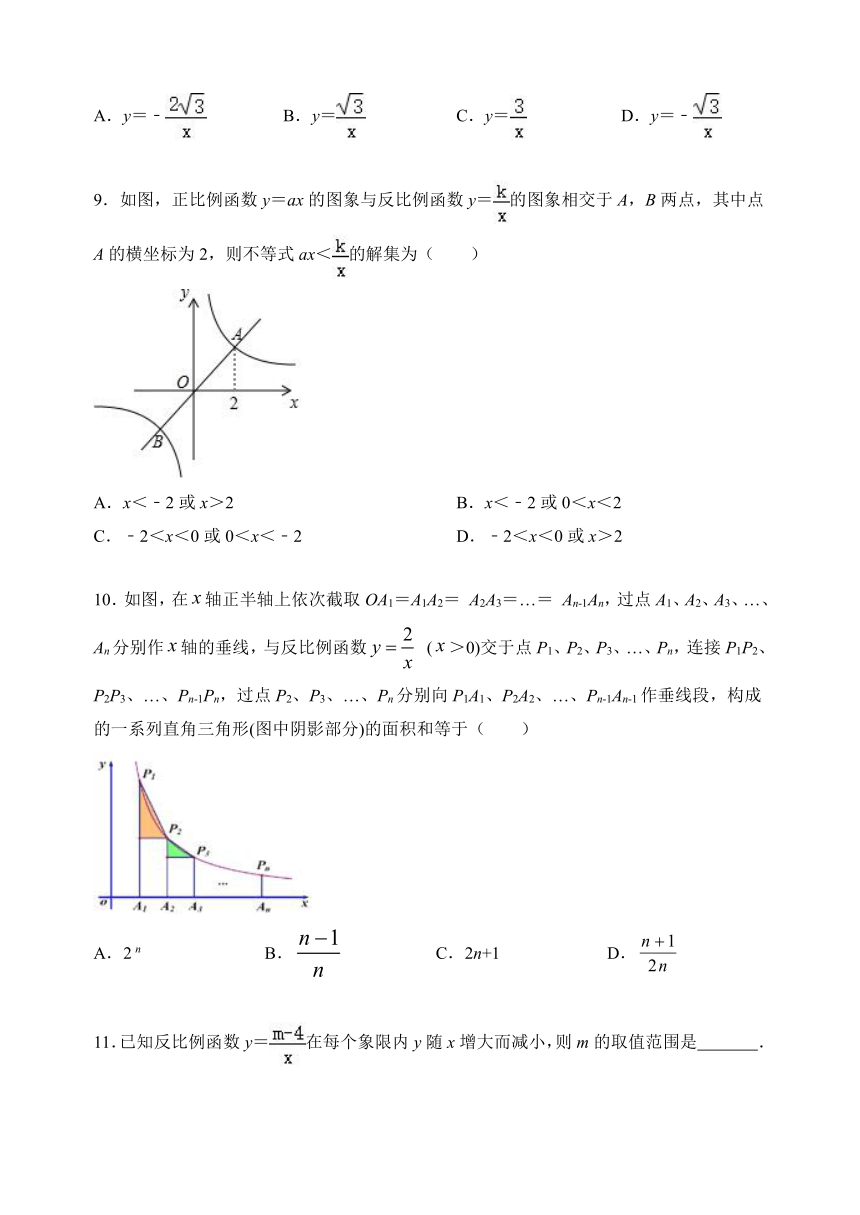
5.已知y是x的反比例函数,并且当x=2时,y=6,则y关于x的函数解析式为( )
A.y=
B.y=
C.y=3x
D.y=
6.若函数y=(2m﹣1)x是反比例函数,则m的值是( )
A.﹣1或1
B.小于的任意实数
C.﹣1
D.1
7.如图,一次函数和反比例函数的图象相交于,两点,则使成立的取值范围是( )
A.或
B.或
C.或
D.或
8.如图,已知点A在反比例函数y=的图象上,点B在x轴的正半轴上,且△OAB是面积为的等边三角形,那么这个反比例函数的解析式是( )
A.y=﹣
B.y=
C.y=
D.y=﹣
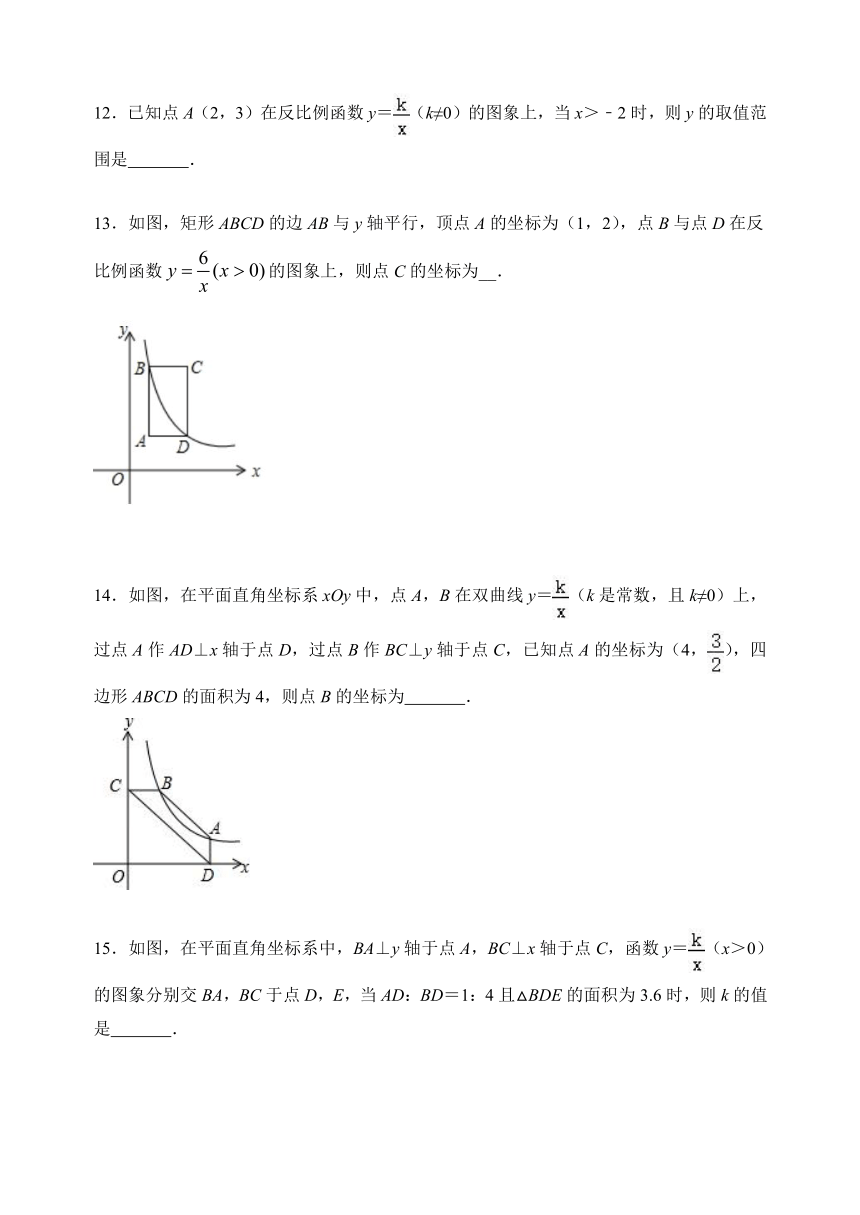
9.如图,正比例函数y=ax的图象与反比例函数y=的图象相交于A,B两点,其中点A的横坐标为2,则不等式ax<的解集为( )
A.x<﹣2或x>2
B.x<﹣2或0<x<2
C.﹣2<x<0或0<x<﹣2
D.﹣2<x<0或x>2
10.如图,在轴正半轴上依次截取OA1=A1A2=
A2A3=…=
An-1An,过点A1、A2、A3、…、An分别作轴的垂线,与反比例函数
(>0)交于点P1、P2、P3、…、Pn,连接P1P2、P2P3、…、Pn-1Pn,过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn-1An-1作垂线段,构成的一系列直角三角形(图中阴影部分)的面积和等于(
)
A.2
B.
C.2n+1
D.
11.已知反比例函数y=在每个象限内y随x增大而减小,则m的取值范围是
.
12.已知点A(2,3)在反比例函数y=(k≠0)的图象上,当x>﹣2时,则y的取值范围是
.
13.如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为(1,2),点B与点D在反比例函数的图象上,则点C的坐标为__.
14.如图,在平面直角坐标系xOy中,点A,B在双曲线y=(k是常数,且k≠0)上,过点A作AD⊥x轴于点D,过点B作BC⊥y轴于点C,已知点A的坐标为(4,),四边形ABCD的面积为4,则点B的坐标为
.
15.如图,在平面直角坐标系中,BA⊥y轴于点A,BC⊥x轴于点C,函数y=(x>0)的图象分别交BA,BC于点D,E,当AD:BD=1:4且△BDE的面积为3.6时,则k的值是
.
16.如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与轴交于点A(-2.0),与反比例函数y=(m≠0)的图象交于点B(2,n),连接BO,若S△AOB=4.
(1)求反比例函数和一次函数的表达式:
(2)若直线AB与y轴的交点为C.求△OCB的面积
(3)根据图象,直接写出当x>0时,不等式>kx+b的解集.
17.反比例函数(k为常数.且k≠0)的图象经过点A(1,3),B(3,m).
(1)求反比例函数的解析式及B点的坐标;
(2)在x轴上找一点P.使PA+PB的值最小,
①求满足条件的点P的坐标;
②求△PAB的面积.
18.如图,正比例函数y=2x的图象与反比例函数y=的图象交于A,B两点,过点A作AC垂直x轴于点C,连接BC.若△ABC的面积为2.
(1)求k的值;
(2)直接写出>2x时,自变量x的取值范围.
19.超越公司将某品牌农副产品运往新时代市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时)
75
80
85
90
95
t(小时)
4.00
3.75
3.53
3.33
3.16
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从超越公司出发,能否在上午10:00之前到达新时代市场?请说明理由
20.如图,在平面直角坐标系中,菱形OABC的顶点A,C在反比例函数y=图象上,直线AC交OB于点D,交x,y正半轴于点E,F,且OE=OF=3
(1)求OB的长;
(2)若AB=,求k的值.
21.某气球内充满了一定量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求这一函数的解析式;
(2)当气体体积为1m3时,气压是多少?
(3)当气球内的气压大于140kPa时,气球将爆炸,为了安全起见,气体的体积应不小于多少?(精确到0.01m3)
参考答案
1.
D
2.
C
3.
C
4.
B
5.
D
6.
A
7.
B
8.
D
9.
B
10.
B
11.
m>4
12.
y<﹣3或y>0
13.
(3,6)
14.
(,)
15.
2.25
16.
解:(1)由A(-2,0),得OA=2;
∵点B(2,n)在第一象限内,S△AOB=4,
∴OA?n=4;
∴n=4;
∴点B的坐标是(2,4);
将点B的坐标(2,4)代入反比例函数,得,
∴m=8;
∴反比例函数的解析式为:y=;
将点A(2,0),B(2,4)的坐标分别代入y=kx+b,得
,
解得;
∴一次函数的表达式y=x+2.
(2)在y=x+2中,令x=0,得y=2,
∴点C的坐标是(0,2),
∴OC=2,
∴S△OCB=×2×2=2.
(3)由于B点坐标为(2,4),可知不等式的解集0<x<2.
故答案为(1)y=,y=x+2;(2)S△OCB=2;(3)0<x<2.
17.
解:(1)把A(1,3)代入y=得,k=3,
∴反比例函数的关系式为:y=;
把B(3,m)代入y=得,m=1,
∴点B的坐标为(3,1);
(2)①如图所示,作点B关于x轴的对称点B′,则B′(3,﹣1),连接AB′交x轴于点P点,此时PA+PB最小.
设直线AB′的关系式为y=kx+b,把A(1,3),B′(3,﹣1)代入得,
,解得,,
∴直线AB′的关系式为y=﹣2x+5,
当y=0时,x=,即:P(,0),也就是,OP=,
②S△PAB=S梯形ABNM﹣S△AMP﹣S△BPN=(1+3)×2﹣(﹣1)×3﹣(3﹣)×1=.
18.
解:(1)设点A的坐标为(m,n).
∵点A在直线y=2x上,∴n=2m.
根据对称性可得OA=OB,
∴S△ABC=2S△ACO=2,
∴S△ACO=1,
∴m?2m=1,
∴m=1(舍负),
∴点A的坐标为(1,2),
∴k=1×2=2;
(2)如图,
由点A与点B关于点O成中心对称得点B(﹣1,﹣2).
结合图象可得:不等式>2x的解集为x<﹣1或0<x<1.
19.
(1)根据表格中数据,可知V=,
∵v=75时,t=4,
∴k=75×4=300
∴V=
经检验,其它数据满足该函数关系式.
(2)不能
∵10﹣7.5=2.5
∴t=2.5时,V==120>100,
∴汽车上午7:30从超越公司出发,不能在上午10:00之前到达新时代市场
20.
解:(1)∵OE=OF=3,
∴EF==6,∠OEF=∠OFE=45°,
∵菱形OABC,
∴OA=AB=BC=CO,OB⊥AC,DC=DA,DO=DB,
∴△DOE为等腰直角三角形,∴DO=DE=EF=3,
∴OB=2DO=6;
答:OB的长为6.
(2)过点A作AN⊥OE,垂足为N,则△ANE是等腰直角三角形,
∴AN=NE
设AN=x,则NE=x,ON=﹣x,
在Rt△AON中,由勾股定理得:
(﹣x)2+x2=()2,解得:x1=,x2=
当x1=时,A(,),C(,)
当x2=时,C(,),A(,)
因此:k==4
答:k的值为:4.
21.
解:(1)设,
由题意知,
所以k=96,
故;
(2)当v=1m3时,;
(3)当p=140kPa时,.
所以为了安全起见,气体的体积应不少于0.69m3.
反比例函数
1.若双曲线y=在每一个象限内,y随x的增大而减小,则k的取值范围是( )
A.k≠3
B.k<3
C.k≥3
D.k>3
2.若ab>0,则一次函数y=ax﹣b与反比例函数y=在同一坐标系数中的大致图象是( )
A.
B.
C.
D.
3.如图,点的坐标是是等边三角形,点在第一象限.若反比例函数的图象经过点,则的值是(
)
A.
B.
C.
D.
4.下列函数是反比例函数的是(
)
A.
B.
C.
D.
5.已知y是x的反比例函数,并且当x=2时,y=6,则y关于x的函数解析式为( )
A.y=
B.y=
C.y=3x
D.y=
6.若函数y=(2m﹣1)x是反比例函数,则m的值是( )
A.﹣1或1
B.小于的任意实数
C.﹣1
D.1
7.如图,一次函数和反比例函数的图象相交于,两点,则使成立的取值范围是( )
A.或
B.或
C.或
D.或
8.如图,已知点A在反比例函数y=的图象上,点B在x轴的正半轴上,且△OAB是面积为的等边三角形,那么这个反比例函数的解析式是( )
A.y=﹣
B.y=
C.y=
D.y=﹣
9.如图,正比例函数y=ax的图象与反比例函数y=的图象相交于A,B两点,其中点A的横坐标为2,则不等式ax<的解集为( )
A.x<﹣2或x>2
B.x<﹣2或0<x<2
C.﹣2<x<0或0<x<﹣2
D.﹣2<x<0或x>2
10.如图,在轴正半轴上依次截取OA1=A1A2=
A2A3=…=
An-1An,过点A1、A2、A3、…、An分别作轴的垂线,与反比例函数
(>0)交于点P1、P2、P3、…、Pn,连接P1P2、P2P3、…、Pn-1Pn,过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn-1An-1作垂线段,构成的一系列直角三角形(图中阴影部分)的面积和等于(
)
A.2
B.
C.2n+1
D.
11.已知反比例函数y=在每个象限内y随x增大而减小,则m的取值范围是
.
12.已知点A(2,3)在反比例函数y=(k≠0)的图象上,当x>﹣2时,则y的取值范围是
.
13.如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为(1,2),点B与点D在反比例函数的图象上,则点C的坐标为__.
14.如图,在平面直角坐标系xOy中,点A,B在双曲线y=(k是常数,且k≠0)上,过点A作AD⊥x轴于点D,过点B作BC⊥y轴于点C,已知点A的坐标为(4,),四边形ABCD的面积为4,则点B的坐标为
.
15.如图,在平面直角坐标系中,BA⊥y轴于点A,BC⊥x轴于点C,函数y=(x>0)的图象分别交BA,BC于点D,E,当AD:BD=1:4且△BDE的面积为3.6时,则k的值是
.
16.如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与轴交于点A(-2.0),与反比例函数y=(m≠0)的图象交于点B(2,n),连接BO,若S△AOB=4.
(1)求反比例函数和一次函数的表达式:
(2)若直线AB与y轴的交点为C.求△OCB的面积
(3)根据图象,直接写出当x>0时,不等式>kx+b的解集.
17.反比例函数(k为常数.且k≠0)的图象经过点A(1,3),B(3,m).
(1)求反比例函数的解析式及B点的坐标;
(2)在x轴上找一点P.使PA+PB的值最小,
①求满足条件的点P的坐标;
②求△PAB的面积.
18.如图,正比例函数y=2x的图象与反比例函数y=的图象交于A,B两点,过点A作AC垂直x轴于点C,连接BC.若△ABC的面积为2.
(1)求k的值;
(2)直接写出>2x时,自变量x的取值范围.
19.超越公司将某品牌农副产品运往新时代市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时)
75
80
85
90
95
t(小时)
4.00
3.75
3.53
3.33
3.16
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从超越公司出发,能否在上午10:00之前到达新时代市场?请说明理由
20.如图,在平面直角坐标系中,菱形OABC的顶点A,C在反比例函数y=图象上,直线AC交OB于点D,交x,y正半轴于点E,F,且OE=OF=3
(1)求OB的长;
(2)若AB=,求k的值.
21.某气球内充满了一定量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求这一函数的解析式;
(2)当气体体积为1m3时,气压是多少?
(3)当气球内的气压大于140kPa时,气球将爆炸,为了安全起见,气体的体积应不小于多少?(精确到0.01m3)
参考答案
1.
D
2.
C
3.
C
4.
B
5.
D
6.
A
7.
B
8.
D
9.
B
10.
B
11.
m>4
12.
y<﹣3或y>0
13.
(3,6)
14.
(,)
15.
2.25
16.
解:(1)由A(-2,0),得OA=2;
∵点B(2,n)在第一象限内,S△AOB=4,
∴OA?n=4;
∴n=4;
∴点B的坐标是(2,4);
将点B的坐标(2,4)代入反比例函数,得,
∴m=8;
∴反比例函数的解析式为:y=;
将点A(2,0),B(2,4)的坐标分别代入y=kx+b,得
,
解得;
∴一次函数的表达式y=x+2.
(2)在y=x+2中,令x=0,得y=2,
∴点C的坐标是(0,2),
∴OC=2,
∴S△OCB=×2×2=2.
(3)由于B点坐标为(2,4),可知不等式的解集0<x<2.
故答案为(1)y=,y=x+2;(2)S△OCB=2;(3)0<x<2.
17.
解:(1)把A(1,3)代入y=得,k=3,
∴反比例函数的关系式为:y=;
把B(3,m)代入y=得,m=1,
∴点B的坐标为(3,1);
(2)①如图所示,作点B关于x轴的对称点B′,则B′(3,﹣1),连接AB′交x轴于点P点,此时PA+PB最小.
设直线AB′的关系式为y=kx+b,把A(1,3),B′(3,﹣1)代入得,
,解得,,
∴直线AB′的关系式为y=﹣2x+5,
当y=0时,x=,即:P(,0),也就是,OP=,
②S△PAB=S梯形ABNM﹣S△AMP﹣S△BPN=(1+3)×2﹣(﹣1)×3﹣(3﹣)×1=.
18.
解:(1)设点A的坐标为(m,n).
∵点A在直线y=2x上,∴n=2m.
根据对称性可得OA=OB,
∴S△ABC=2S△ACO=2,
∴S△ACO=1,
∴m?2m=1,
∴m=1(舍负),
∴点A的坐标为(1,2),
∴k=1×2=2;
(2)如图,
由点A与点B关于点O成中心对称得点B(﹣1,﹣2).
结合图象可得:不等式>2x的解集为x<﹣1或0<x<1.
19.
(1)根据表格中数据,可知V=,
∵v=75时,t=4,
∴k=75×4=300
∴V=
经检验,其它数据满足该函数关系式.
(2)不能
∵10﹣7.5=2.5
∴t=2.5时,V==120>100,
∴汽车上午7:30从超越公司出发,不能在上午10:00之前到达新时代市场
20.
解:(1)∵OE=OF=3,
∴EF==6,∠OEF=∠OFE=45°,
∵菱形OABC,
∴OA=AB=BC=CO,OB⊥AC,DC=DA,DO=DB,
∴△DOE为等腰直角三角形,∴DO=DE=EF=3,
∴OB=2DO=6;
答:OB的长为6.
(2)过点A作AN⊥OE,垂足为N,则△ANE是等腰直角三角形,
∴AN=NE
设AN=x,则NE=x,ON=﹣x,
在Rt△AON中,由勾股定理得:
(﹣x)2+x2=()2,解得:x1=,x2=
当x1=时,A(,),C(,)
当x2=时,C(,),A(,)
因此:k==4
答:k的值为:4.
21.
解:(1)设,
由题意知,
所以k=96,
故;
(2)当v=1m3时,;
(3)当p=140kPa时,.
所以为了安全起见,气体的体积应不少于0.69m3.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
