2020年春苏科版八年级数学下册期末培优复习第9章 平行四边形 (含答案)
文档属性
| 名称 | 2020年春苏科版八年级数学下册期末培优复习第9章 平行四边形 (含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 256.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-07 00:00:00 | ||
图片预览


文档简介
第9章
中心对称图形——平行四边形
1.
下列命题是假命题的是( )
A.平行四边形既是轴对称图形,又是中心对称图形
B.同角(或等角)的余角相等
C.线段垂直平分线上的点到线段两端的距离相等
D.正方形的对角线相等,且互相垂直平分
2.如图,在△ABC中,D,E分别是AB,AC边的中点,若DE=2,则BC的长度是( )
A.6
B.5
C.4
D.3
3.如图,在?ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论不正确的是(
)
A.S△AFD=2S△EFB
B.BF=DF
C.四边形AECD是等腰梯形
D.∠AEB=∠ADC
4.已知平行四边形ABCD的周长为32,AB=4,则BC的长为(
)
A.4
B.12
C.24
D.28
5.
如图,在?ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连结OE.若∠ABC=60°,∠BAC=80°,则∠1的度数为( )
A.50°
B.40°
C.30°
D.20°
6.下列正多边形中,绕其中心旋转72°后,能和自身重合的是( )
A.正方形
B.正五边形
C.正六边形
D.正八边形
7.如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,则△CDE的周长是(
)
A.6
B.8
C.9
D.10
8.
如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于点F,AB=BF.添加一个条件使四边形ABCD是平行四边形,你认为下面四个条件中可选择的是( )
A.AD=BC
B.CD=BF
C.∠A=∠C
D.∠F=∠CDF
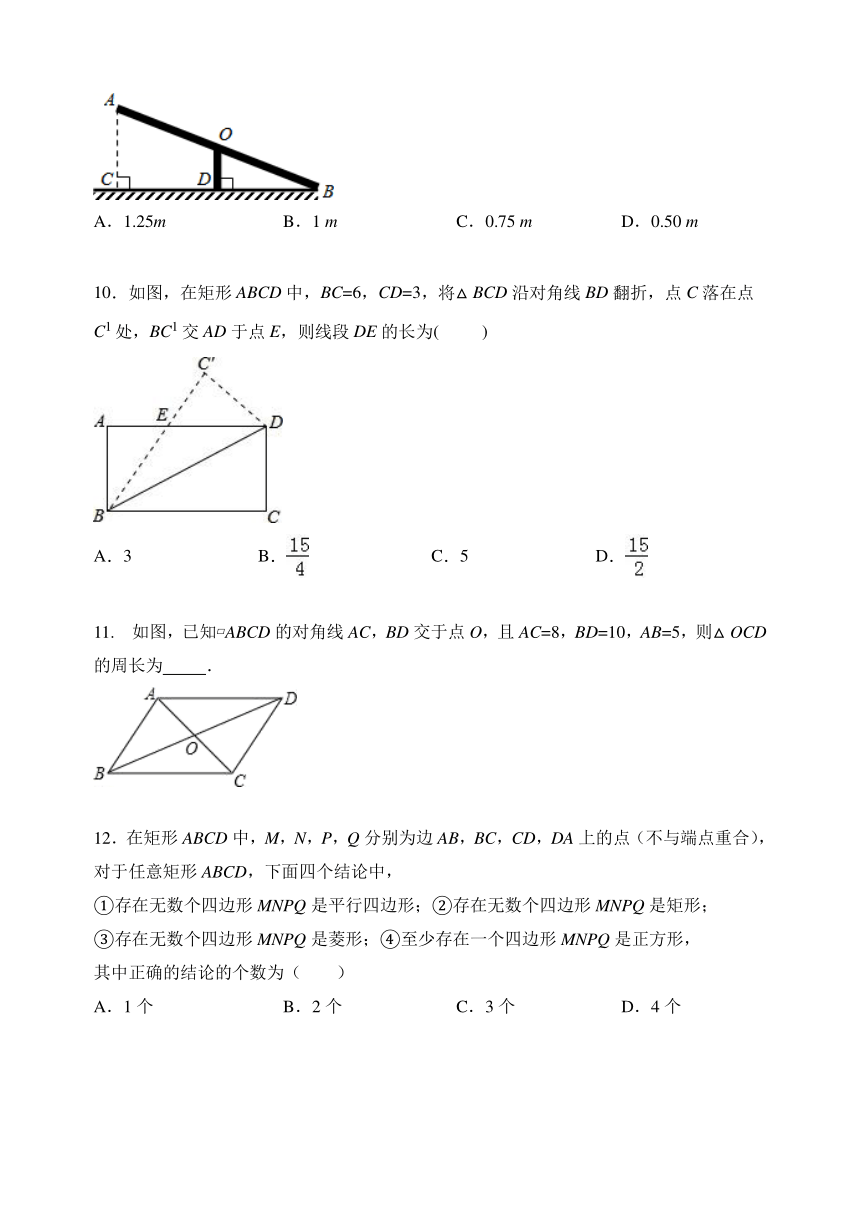
9.如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=0.5m,当它的一端B着地时,另一端A离地面的高度AC为( )
A.1.25m
B.1
m
C.0.75
m
D.0.50
m
10.如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C1处,BC1交AD于点E,则线段DE的长为(
)
A.3
B.
C.5
D.
11.
如图,已知?ABCD的对角线AC,BD交于点O,且AC=8,BD=10,AB=5,则△OCD的周长为
.
12.在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,下面四个结论中,
①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;
③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形,
其中正确的结论的个数为( )
A.1个
B.2个
C.3个
D.4个
13.如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是
.
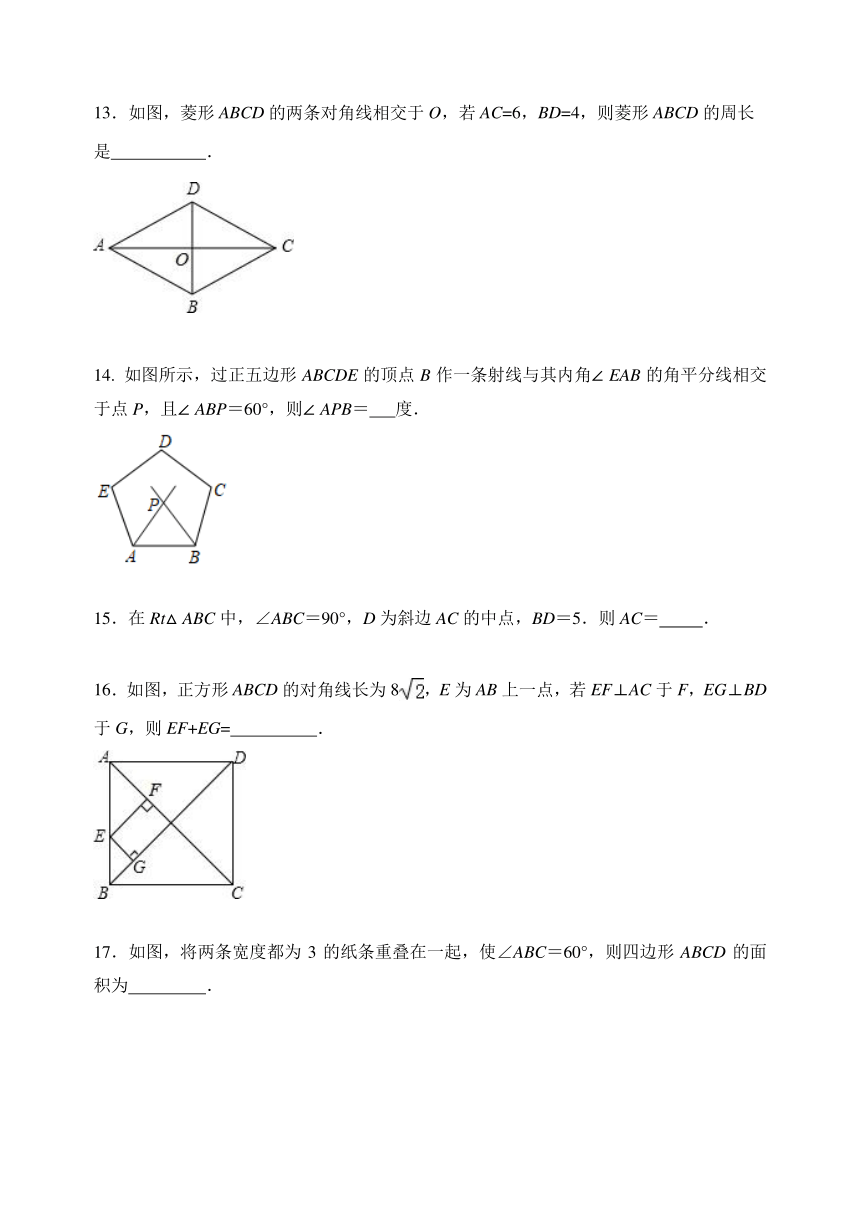
14.
如图所示,过正五边形ABCDE的顶点B作一条射线与其内角∠EAB的角平分线相交于点P,且∠ABP=60°,则∠APB=
度.
15.在Rt△ABC中,∠ABC=90°,D为斜边AC的中点,BD=5.则AC=
.
16.如图,正方形ABCD的对角线长为8,E为AB上一点,若EF⊥AC于F,EG⊥BD于G,则EF+EG=
.
17.如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°,则四边形ABCD的面积为
.
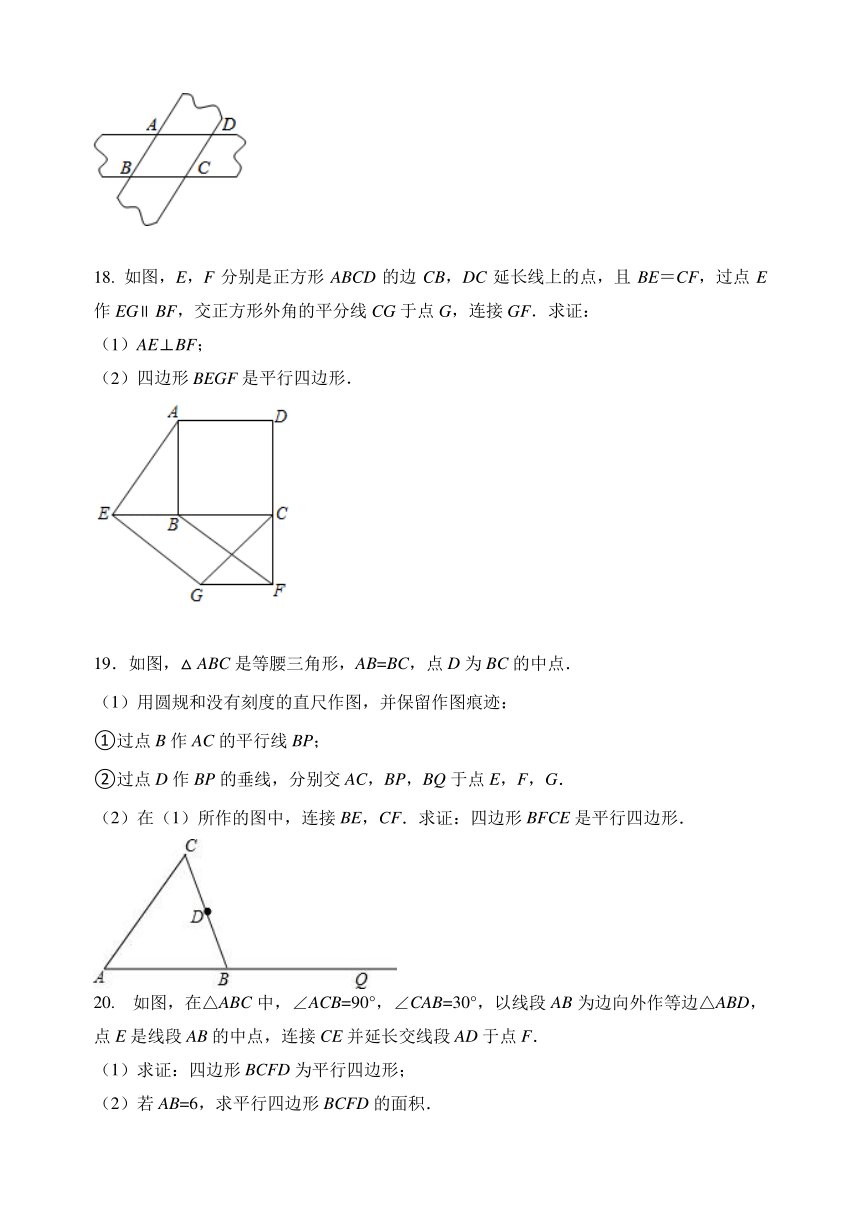
18.
如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作EG∥BF,交正方形外角的平分线CG于点G,连接GF.求证:
(1)AE⊥BF;
(2)四边形BEGF是平行四边形.
19.如图,△ABC是等腰三角形,AB=BC,点D为BC的中点.
(1)用圆规和没有刻度的直尺作图,并保留作图痕迹:
①过点B作AC的平行线BP;
②过点D作BP的垂线,分别交AC,BP,BQ于点E,F,G.
(2)在(1)所作的图中,连接BE,CF.求证:四边形BFCE是平行四边形.
20.
如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)若AB=6,求平行四边形BCFD的面积.
21.把三角形绕A点按顺时针方向旋转90°.画出旋转后的图形.
22.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
求证:四边形OCED是菱形.
23.如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF为菱形;
(2)如果∠A=100°,∠C=30°,求∠BDE的度数.
24.在矩形ABCD中,点E在BC上.DF⊥AE,重足为F,DF=AB.
(1)求证.AE=BC;
(2)若∠FDC=30°,且AB=4,连结DE,求∠DEF的大小和AD.
参考答案
1.
A
2.
C
3.
A
4.
B
5.
B
6.
B
7.
B
8.
D
9.
B
10.
B
11.
14.
12.
C
13.
4.
14.
66
15.
10.
16.
4.
17.
6.
18.
证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°,
∴∠ABE=∠BCF=90°,
在△ABE和△BCF中,,
∴△ABE≌△BCF(SAS),
∴AE=BF,∠BAE=∠CBF,
∵EG∥BF,
∴∠CBF=∠CEG,
∵∠BAE+∠BEA=90°,
∴∠CEG+∠BEA=90°,
∴AE⊥EG,
∴AE⊥BF;
(2)延长AB至点P,使BP=BE,连接EP,如图所示:
则AP=CE,∠EBP=90°,
∴∠P=45°,
∵CG为正方形ABCD外角的平分线,
∴∠ECG=45°,
∴∠P=∠ECG,
由(1)得∠BAE=∠CEG,
在△APE和△ECG中,,
∴△APE≌△ECG(ASA),
∴AE=EG,
∵AE=BF,
∴EG=BF,
∵EG∥BF,
∴四边形BEGF是平行四边形.
19.
解:(1)如图:
(2)证明:如图:
∵BP∥AC,
∴∠ACB=∠PBC,
在△ECD和△FBD中,
,
∴△ECD≌△FBD,
∴CE=BF,
∴四边形ECFB是平行四边形.
20.
(1)证明:在△ABC中,∠ACB=90°,∠CAB=30°,
∴∠ABC=60°.
在等边△ABD中,∠BAD=60°,
∴∠BAD=∠ABC=60°.
∵E为AB的中点,
∴AE=BE.
又∵∠AEF=∠BEC,
∴△AEF≌△BEC.
在△ABC中,∠ACB=90°,E为AB的中点,
∴CE=AB,BE=AB.
∴CE=AE,
∴∠EAC=∠ECA=30°,
∴∠BCE=∠EBC=60°.
又∵△AEF≌△BEC,
∴∠AFE=∠BCE=60°.
又∵∠D=60°,
∴∠AFE=∠D=60°.
∴FC∥BD.
又∵∠BAD=∠ABC=60°,
∴AD∥BC,即FD∥BC.
∴四边形BCFD是平行四边形.
(2)解:在Rt△ABC中,∵∠BAC=30°,AB=6,
∴BC=AB=3,AC=BC=3,
∴S平行四边形BCFD=3×=9.
21.
解:如图,△AB′C′为所作.
22.
证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∵四边形ABCD是矩形,
∴OC=OD,
∴四边形OCED是菱形.
23.
(1)证明:∵DE∥BC,DF∥AB
∴四边形DEBF是平行四边形
∵DE∥BC
∴∠EDB=∠DBF
∵BD平分∠ABC
∴∠ABD=∠DBF=∠ABC
∴∠ABD=∠EDB
∴DE=BE且四边形BEDF为平行四边形
∴四边形BEDF为菱形;
(2)解:∵∠A=100°,∠C=30°,
∴∠ABC=180°﹣100°﹣30°=50°,
∵四边形BEDF为菱形,
∴∠EDF=∠ABC=50°,∠BDE=∠EDF=25°.
24.
(1)证明:∵四边形ABCD是矩形,
∴DA∥BC,∠B=∠ADC,
∴∠DAE=∠AEB,
∴在△ABE与△DFA中,
∴△ABE≌△DFA(AAS),
∴AE=AD,
∵AD=BC,
∴AE=BC;
(2)解:∵DF⊥AE,∠C=90°,
∴∠DFE∥∠DCE,
∵AB=DF,且AB=DC,
∴DF=DC,
∴在Rt△DEF与Rt△DCE中,
∴Rt△DEF≌Rt△DCE(HL),
∴∠FDE=∠CDE,
∵∠FDC=30°,
∴∠FDE=∠CDE=30°÷2=15°,
∴∠DEF=180°﹣90°﹣15°=75°,
∵△ABE≌△DFA,AB=4,
∴DF=4,
∵∠FDC=30°,
∴∠ADF=90°﹣30°=60°,
∴∠DAE=180°﹣90°﹣60°=30°,
∵∠DF=4,
∴AD=4×2=8,
∴∠DEF=75°,AD=8.
中心对称图形——平行四边形
1.
下列命题是假命题的是( )
A.平行四边形既是轴对称图形,又是中心对称图形
B.同角(或等角)的余角相等
C.线段垂直平分线上的点到线段两端的距离相等
D.正方形的对角线相等,且互相垂直平分
2.如图,在△ABC中,D,E分别是AB,AC边的中点,若DE=2,则BC的长度是( )
A.6
B.5
C.4
D.3
3.如图,在?ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论不正确的是(
)
A.S△AFD=2S△EFB
B.BF=DF
C.四边形AECD是等腰梯形
D.∠AEB=∠ADC
4.已知平行四边形ABCD的周长为32,AB=4,则BC的长为(
)
A.4
B.12
C.24
D.28
5.
如图,在?ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连结OE.若∠ABC=60°,∠BAC=80°,则∠1的度数为( )
A.50°
B.40°
C.30°
D.20°
6.下列正多边形中,绕其中心旋转72°后,能和自身重合的是( )
A.正方形
B.正五边形
C.正六边形
D.正八边形
7.如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,则△CDE的周长是(
)
A.6
B.8
C.9
D.10
8.
如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于点F,AB=BF.添加一个条件使四边形ABCD是平行四边形,你认为下面四个条件中可选择的是( )
A.AD=BC
B.CD=BF
C.∠A=∠C
D.∠F=∠CDF
9.如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=0.5m,当它的一端B着地时,另一端A离地面的高度AC为( )
A.1.25m
B.1
m
C.0.75
m
D.0.50
m
10.如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C1处,BC1交AD于点E,则线段DE的长为(
)
A.3
B.
C.5
D.
11.
如图,已知?ABCD的对角线AC,BD交于点O,且AC=8,BD=10,AB=5,则△OCD的周长为
.
12.在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,下面四个结论中,
①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;
③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形,
其中正确的结论的个数为( )
A.1个
B.2个
C.3个
D.4个
13.如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是
.
14.
如图所示,过正五边形ABCDE的顶点B作一条射线与其内角∠EAB的角平分线相交于点P,且∠ABP=60°,则∠APB=
度.
15.在Rt△ABC中,∠ABC=90°,D为斜边AC的中点,BD=5.则AC=
.
16.如图,正方形ABCD的对角线长为8,E为AB上一点,若EF⊥AC于F,EG⊥BD于G,则EF+EG=
.
17.如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°,则四边形ABCD的面积为
.
18.
如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作EG∥BF,交正方形外角的平分线CG于点G,连接GF.求证:
(1)AE⊥BF;
(2)四边形BEGF是平行四边形.
19.如图,△ABC是等腰三角形,AB=BC,点D为BC的中点.
(1)用圆规和没有刻度的直尺作图,并保留作图痕迹:
①过点B作AC的平行线BP;
②过点D作BP的垂线,分别交AC,BP,BQ于点E,F,G.
(2)在(1)所作的图中,连接BE,CF.求证:四边形BFCE是平行四边形.
20.
如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)若AB=6,求平行四边形BCFD的面积.
21.把三角形绕A点按顺时针方向旋转90°.画出旋转后的图形.
22.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
求证:四边形OCED是菱形.
23.如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF为菱形;
(2)如果∠A=100°,∠C=30°,求∠BDE的度数.
24.在矩形ABCD中,点E在BC上.DF⊥AE,重足为F,DF=AB.
(1)求证.AE=BC;
(2)若∠FDC=30°,且AB=4,连结DE,求∠DEF的大小和AD.
参考答案
1.
A
2.
C
3.
A
4.
B
5.
B
6.
B
7.
B
8.
D
9.
B
10.
B
11.
14.
12.
C
13.
4.
14.
66
15.
10.
16.
4.
17.
6.
18.
证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°,
∴∠ABE=∠BCF=90°,
在△ABE和△BCF中,,
∴△ABE≌△BCF(SAS),
∴AE=BF,∠BAE=∠CBF,
∵EG∥BF,
∴∠CBF=∠CEG,
∵∠BAE+∠BEA=90°,
∴∠CEG+∠BEA=90°,
∴AE⊥EG,
∴AE⊥BF;
(2)延长AB至点P,使BP=BE,连接EP,如图所示:
则AP=CE,∠EBP=90°,
∴∠P=45°,
∵CG为正方形ABCD外角的平分线,
∴∠ECG=45°,
∴∠P=∠ECG,
由(1)得∠BAE=∠CEG,
在△APE和△ECG中,,
∴△APE≌△ECG(ASA),
∴AE=EG,
∵AE=BF,
∴EG=BF,
∵EG∥BF,
∴四边形BEGF是平行四边形.
19.
解:(1)如图:
(2)证明:如图:
∵BP∥AC,
∴∠ACB=∠PBC,
在△ECD和△FBD中,
,
∴△ECD≌△FBD,
∴CE=BF,
∴四边形ECFB是平行四边形.
20.
(1)证明:在△ABC中,∠ACB=90°,∠CAB=30°,
∴∠ABC=60°.
在等边△ABD中,∠BAD=60°,
∴∠BAD=∠ABC=60°.
∵E为AB的中点,
∴AE=BE.
又∵∠AEF=∠BEC,
∴△AEF≌△BEC.
在△ABC中,∠ACB=90°,E为AB的中点,
∴CE=AB,BE=AB.
∴CE=AE,
∴∠EAC=∠ECA=30°,
∴∠BCE=∠EBC=60°.
又∵△AEF≌△BEC,
∴∠AFE=∠BCE=60°.
又∵∠D=60°,
∴∠AFE=∠D=60°.
∴FC∥BD.
又∵∠BAD=∠ABC=60°,
∴AD∥BC,即FD∥BC.
∴四边形BCFD是平行四边形.
(2)解:在Rt△ABC中,∵∠BAC=30°,AB=6,
∴BC=AB=3,AC=BC=3,
∴S平行四边形BCFD=3×=9.
21.
解:如图,△AB′C′为所作.
22.
证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∵四边形ABCD是矩形,
∴OC=OD,
∴四边形OCED是菱形.
23.
(1)证明:∵DE∥BC,DF∥AB
∴四边形DEBF是平行四边形
∵DE∥BC
∴∠EDB=∠DBF
∵BD平分∠ABC
∴∠ABD=∠DBF=∠ABC
∴∠ABD=∠EDB
∴DE=BE且四边形BEDF为平行四边形
∴四边形BEDF为菱形;
(2)解:∵∠A=100°,∠C=30°,
∴∠ABC=180°﹣100°﹣30°=50°,
∵四边形BEDF为菱形,
∴∠EDF=∠ABC=50°,∠BDE=∠EDF=25°.
24.
(1)证明:∵四边形ABCD是矩形,
∴DA∥BC,∠B=∠ADC,
∴∠DAE=∠AEB,
∴在△ABE与△DFA中,
∴△ABE≌△DFA(AAS),
∴AE=AD,
∵AD=BC,
∴AE=BC;
(2)解:∵DF⊥AE,∠C=90°,
∴∠DFE∥∠DCE,
∵AB=DF,且AB=DC,
∴DF=DC,
∴在Rt△DEF与Rt△DCE中,
∴Rt△DEF≌Rt△DCE(HL),
∴∠FDE=∠CDE,
∵∠FDC=30°,
∴∠FDE=∠CDE=30°÷2=15°,
∴∠DEF=180°﹣90°﹣15°=75°,
∵△ABE≌△DFA,AB=4,
∴DF=4,
∵∠FDC=30°,
∴∠ADF=90°﹣30°=60°,
∴∠DAE=180°﹣90°﹣60°=30°,
∵∠DF=4,
∴AD=4×2=8,
∴∠DEF=75°,AD=8.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
