2020年春苏科版八年级数学下册期末培优复习第8章 认识概率 (含答案)
文档属性
| 名称 | 2020年春苏科版八年级数学下册期末培优复习第8章 认识概率 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 464.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-07 23:29:23 | ||
图片预览



文档简介
第8章
认识概率
1.下列事件中,随机事件是
A.经过有交通信号灯的路口,遇到红灯
B.实心铁球投入水中会沉入水底
C.一滴花生油滴入水中,油会浮在水面
D.两负数的和为正数
2.甲袋中装有形状、大小与质地都相同的红球3个,乙袋中装有形状、大小与质地都相同的红球2个,黄球1个,下列事件为随机事件的是(
)
A.
从甲袋中随机摸出1个球,是黄球
B.
从甲袋中随机摸出1个球,是红球
C.
从乙袋中随机摸出1个球,是红球或黄球
D.
从乙袋中随机摸出1个球,是黄球
3.某科研小组,为了考查某河野生鱼的数量,从中捕捞200条,作上标记后,放回河里,经过一段时间,再从中捕捞300条,发现有标记的鱼有15条,则估计该河中野生鱼有(
)
A.8000条
B.4000条
C.2000条
D.1000条
4.不透明的袋子中只有4个黑球和2个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件是不可能事件的是(
)
A.3个球都是黑球
B.3个球都是白球
C.三个球中有黑球
D.3个球中有白球
5.下列事件中,属于不可能事件的是
A.某个数的绝对值大于0
B.某个数的相反数等于它本身
C.任意一个五边形的外角和等于
D.长分别为3,4,6的三条线段能围成一个三角形
6.下列事件是不可能事件的是(
)
A.
明天会下雨
B.
小明数学成绩是99分
C.
一个数与它的相反数的和是0
D.
明年一年共有367天
7.下列事件:①经过有交通信号灯的路口,遇到红灯;②掷一枚均匀的正方体骰子,骰子落地后朝上的点数不是奇数便是偶数;③长为5cm、5cm、11cm的三条线段能围成一个三角形;④买一张体育彩票中奖。其中随机事件有(
)
A.1个
B.2个
C.3个
D.4个
8.某班组织了针对全班同学关于“你最喜欢的一项体育活动”的问卷调查后,绘制出频数分布直方图,由图可知,下列结论正确的是
A.最喜欢篮球的人数最多
B.最喜欢羽毛球的人数是最喜欢乒乓球人数的两倍
C.全班共有50名学生
D.最喜欢田径的人数占总人数的
9.某彩票中奖机会是,现有人购1000张,则该人中奖机会是(
)
A.
B.
不可能中奖
C.
中奖机会大
D.
不能确定
10.下列4个对事件的判断中,所有正确结论的序号是( )
①“哥哥的年龄比弟弟的年龄大”是必然事件;②“书柜里有6本大小相同,厚度差不多的书,从中随机摸出一本是小说”是随机事件;③在1万次试验中,每次都不发生的事件是不可能事件;④在1万次试验中,每次都发生的事件是必然事件.
A.①
B.①②
C.①③④
D.①②③④
11.秋季新学期开学时,某中学对六年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了不完整的图表(如表所示),图表中
.
分 数 段
频数
频率
6
20
0.4
15
0.18
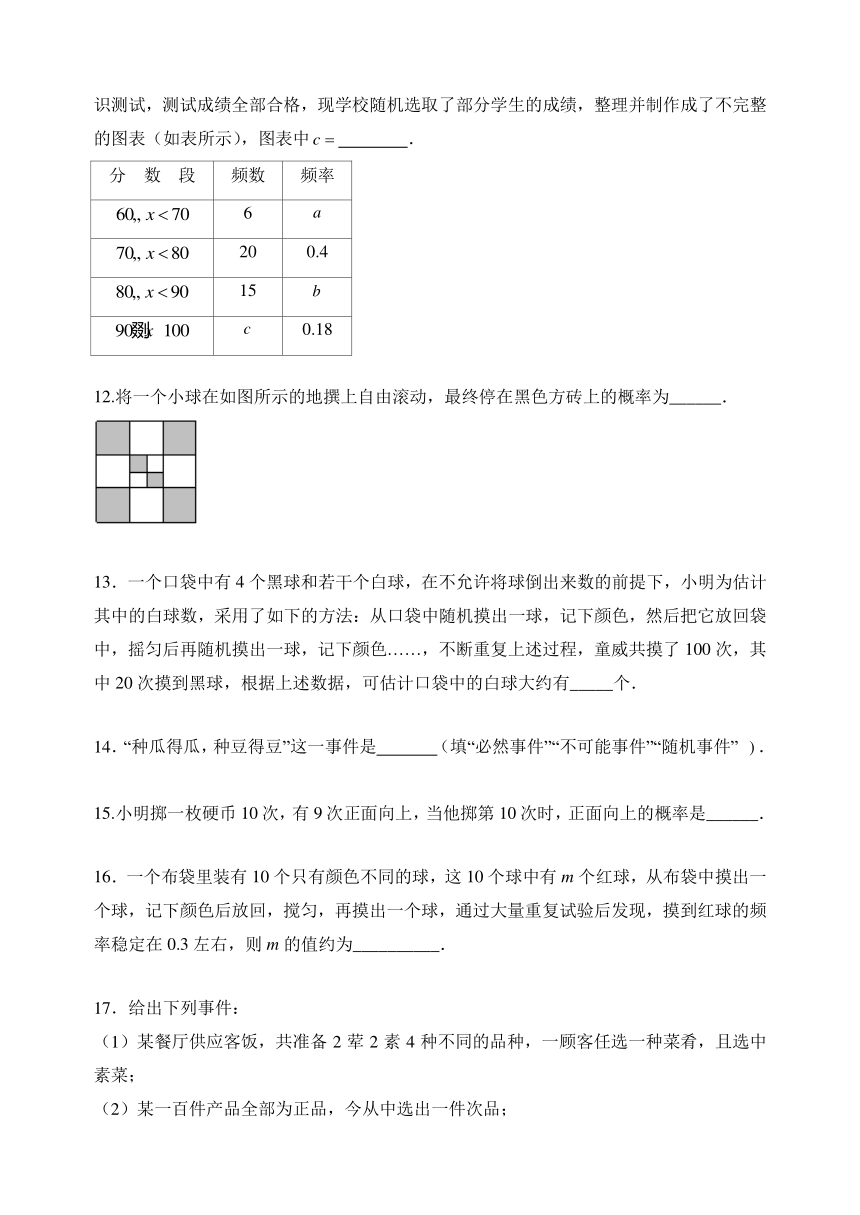
12.将一个小球在如图所示的地撰上自由滚动,最终停在黑色方砖上的概率为______.
13.一个口袋中有4个黑球和若干个白球,在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回袋中,摇匀后再随机摸出一球,记下颜色……,不断重复上述过程,童威共摸了100次,其中20次摸到黑球,根据上述数据,可估计口袋中的白球大约有_____个.
14.“种瓜得瓜,种豆得豆”这一事件是
(填“必然事件”“不可能事件”“随机事件”
.
15.小明掷一枚硬币10次,有9次正面向上,当他掷第10次时,正面向上的概率是______.
16.一个布袋里装有10个只有颜色不同的球,这10个球中有m个红球,从布袋中摸出一个球,记下颜色后放回,搅匀,再摸出一个球,通过大量重复试验后发现,摸到红球的频率稳定在0.3左右,则m的值约为__________.
17.给出下列事件:
(1)某餐厅供应客饭,共准备2荤2素4种不同的品种,一顾客任选一种菜肴,且选中素菜;
(2)某一百件产品全部为正品,今从中选出一件次品;
(3)在1,2,3,4,5五条线路停靠的车站上,张老师等候到6路车;
(4)七人排成一排照相,甲、乙正好相邻;
(5)在有30个空位的电影院里,小红找到了一个空位,
请将事件的序号填写在横线上:
必然事件
,不可能事件
,不确定事件
.
18.在不透明的口袋中有若干个完全一样的红色小球,现放入10个仅颜色不同的白色小球,均匀混合后,有放回地随机摸取30次,有10次摸到白色小球,据此估计该口袋中原有红色小球个数为??????????.
19.在一个不透明的盒子中装有n个小球,它们除了颜色不同外,其余都相同,其中有4个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.大量重复上述试验后发现,摸到白球的频率稳定在0.4,那么可以推算出n的值大约是_______.
20.下面第一排表示十张扑克牌的不同情况,任意摸一张,请你将摸到红色扑克牌的可能性与对应的方框用线连起来.
21.一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外其余都相同.
(1)从袋中随机摸出一个球,记录其颜色,然后放回,大量重复该实验,发现摸到绿球的频率稳定于,求n的值;
(2)小明与小华进行摸球游戏,小明用摸出一球后,不放回,小华在摸出一球,若两次摸出的球颜色不同的则小明获胜,否则为小华获胜,试通过计算说明这个游戏是否公平.
22.下列事件中,哪些是必然事件?哪些是不可能事件?哪些是随机事件?
(1)太阳从西边落山;
(2)某人的体温是100
℃;
(3)a2+b2=0;
(4)某个等腰三角形中任意两个角都不相等;
(5)经过有信号灯的十字路口,遇见红灯.
23.甲乙两人玩“锤子、石头、剪子、布”游戏,他们在不透明的袋子中放入形状、大小均相同的22张卡片,其中写有“锤子”石头”、“剪子”、“布”的卡片张数分别为4、5、6、7.两人先后各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:
“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负.
(1)若甲先摸,则他摸出“剪子”的概率是多少?
(2)若甲先摸出了“剪子”,则乙获胜的概率是多少?
(3)若甲先摸,则他摸出哪种卡片获胜的可能性最大?
24.在一个不透明的盒子里装有红、黑两种颜色的球共60只,这些球除颜色外其余完全相同.为了估计红球和黑球的个数,七班的数学学习小组做了摸球实验.他们将球搅匀后,从盒子里随机摸出一个球记下颜色,再把球放回盒子中,多次重复上述过程,得到下表中的一组统计数据:
摸球的次数n
50
100
300
500
800
1000
2000
摸到红球的次数m
14
33
95
155
241
298
602
摸到红球的频率
(1)请估计:当次数n足够大时,摸到红球的频率将会接近______;精确到
(2)假如你去摸一次,则摸到红球的概率的估计值为______;
(3)试估算盒子里红球的数量为______个,黑球的数量为______
25.2019年女排世界杯中,中国女排以11站全胜且只丢3局的成绩成功卫冕本届世界杯冠军.某校七年级为了弘扬女排精神,组建了排球社团,通过测量同学们的身高(单位:cm),并绘制了如下两幅不完整的统计图,请结合图中提供的信息,解答下列问题.
(1)填空:样本容量为___,a=___;
(2)把频数分布直方图补充完整;
(3)若从该组随机抽取1名学生,估计这名学生身高低于165cm的概率.
26.在一个不透明的盒子里装有黑、白两种颜色的球共50个,这些球除颜色外其余完全相同.王颖做摸球试验,搅匀后,她从盒子里随机摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程,如表是试验中的一组统计数据:
摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
65
124
178
302
480
600
1800
摸到白球的频率
0.65
0.62
0.593
0.604
0.6
0.6
0.6
(1)请估计:当n很大时,摸到白球的频率将会接近
;(精确到0.1)
(2)若从盒子里随机摸出一个球,则摸到白球的概率的估计值为
;
(3)试估算盒子里黑、白两种颜色的球各有多少个?
参考答案
1.
A
2.
D
3.
B
4.
B
5.
C
6.
D
7.
B
8.
C
9.
C
10.
A
11.
9
12.
1/2
13.
16.
14.
必然事件 .
15.
1/2
16.
3
17.
(5) , (2)(3)
, (1)(4)
.
18.
20
19.
10
20.
21.
解:利用频率估计概率得到摸到绿球的概率为,
则,
解得;
画树状图为:
共有12种等可能的结果数,其中两次摸出的球的颜色不同的结果共有10?种,
所以两次摸出的球颜色不同的概率,
则小明胜的概率为、小华胜的概率为,
所以这个游戏不公平.
22.
(1)
“太阳从西边落山”是必然事件;(2)
“某人的体温是100
℃”是不可能事件;(3)
“a2+b2=0”是随机事件;(4)
“某个等腰三角形中任意两个角都不相等”是不可能事件;(5)
“经过有信号灯的十字路口,遇见红灯”是随机事件.
23.
(1)甲先摸,则他摸出“剪子”的概率.
(2)甲先摸出了“剪子”,不透明的袋子中有“锤子”石头”、“剪子”、“布”的卡片张数分别为4、5、5、7,
乙要获胜需要抽出“锤子”胜“石头”,乙获胜的概率.
(3)甲先摸出了“锤子”并且获胜,乙需要摸出”,“石头”或“剪子”,甲胜的概率
甲先摸出了“石头”并且获胜,乙需要摸出”“剪子”,甲胜的概率
甲先摸出了“剪子”并且获胜,乙需要摸出“布”,甲胜的概率
甲先摸出了“布”并且获胜,乙需要摸出“锤子”和“石头”,甲胜的概率,
其中最大,所以甲先摸出了“锤子”获胜的概率最大.
24.
解:当次数n足够大时,摸到红球的频率将会接近,故答案为;
摸到红球的概率的估计值为,故答案为;
估算盒子里红球的数量为个,黑球的个数为个,故答案为18;42.
25.
解:(1)15÷
=100,
所以样本容量为100;
B组的人数为100-15-35-15-5=30,
所以a%=
×100%=30%,则a=30;
故答案为100,30;
(2)补全频数分布直方图为:
(3)样本中身高低于165cm的人数为15+30+35=80,
样本中身高低于165cm的频率为,
所以估计从该地随机抽取1名学生,估计这名学生身高低于165cm的概率为.
26.
(1)0.6;(2)0.6;(3)盒子里黑颜色的球有20只,盒子白颜色的球有30只
认识概率
1.下列事件中,随机事件是
A.经过有交通信号灯的路口,遇到红灯
B.实心铁球投入水中会沉入水底
C.一滴花生油滴入水中,油会浮在水面
D.两负数的和为正数
2.甲袋中装有形状、大小与质地都相同的红球3个,乙袋中装有形状、大小与质地都相同的红球2个,黄球1个,下列事件为随机事件的是(
)
A.
从甲袋中随机摸出1个球,是黄球
B.
从甲袋中随机摸出1个球,是红球
C.
从乙袋中随机摸出1个球,是红球或黄球
D.
从乙袋中随机摸出1个球,是黄球
3.某科研小组,为了考查某河野生鱼的数量,从中捕捞200条,作上标记后,放回河里,经过一段时间,再从中捕捞300条,发现有标记的鱼有15条,则估计该河中野生鱼有(
)
A.8000条
B.4000条
C.2000条
D.1000条
4.不透明的袋子中只有4个黑球和2个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件是不可能事件的是(
)
A.3个球都是黑球
B.3个球都是白球
C.三个球中有黑球
D.3个球中有白球
5.下列事件中,属于不可能事件的是
A.某个数的绝对值大于0
B.某个数的相反数等于它本身
C.任意一个五边形的外角和等于
D.长分别为3,4,6的三条线段能围成一个三角形
6.下列事件是不可能事件的是(
)
A.
明天会下雨
B.
小明数学成绩是99分
C.
一个数与它的相反数的和是0
D.
明年一年共有367天
7.下列事件:①经过有交通信号灯的路口,遇到红灯;②掷一枚均匀的正方体骰子,骰子落地后朝上的点数不是奇数便是偶数;③长为5cm、5cm、11cm的三条线段能围成一个三角形;④买一张体育彩票中奖。其中随机事件有(
)
A.1个
B.2个
C.3个
D.4个
8.某班组织了针对全班同学关于“你最喜欢的一项体育活动”的问卷调查后,绘制出频数分布直方图,由图可知,下列结论正确的是
A.最喜欢篮球的人数最多
B.最喜欢羽毛球的人数是最喜欢乒乓球人数的两倍
C.全班共有50名学生
D.最喜欢田径的人数占总人数的
9.某彩票中奖机会是,现有人购1000张,则该人中奖机会是(
)
A.
B.
不可能中奖
C.
中奖机会大
D.
不能确定
10.下列4个对事件的判断中,所有正确结论的序号是( )
①“哥哥的年龄比弟弟的年龄大”是必然事件;②“书柜里有6本大小相同,厚度差不多的书,从中随机摸出一本是小说”是随机事件;③在1万次试验中,每次都不发生的事件是不可能事件;④在1万次试验中,每次都发生的事件是必然事件.
A.①
B.①②
C.①③④
D.①②③④
11.秋季新学期开学时,某中学对六年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了不完整的图表(如表所示),图表中
.
分 数 段
频数
频率
6
20
0.4
15
0.18
12.将一个小球在如图所示的地撰上自由滚动,最终停在黑色方砖上的概率为______.
13.一个口袋中有4个黑球和若干个白球,在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回袋中,摇匀后再随机摸出一球,记下颜色……,不断重复上述过程,童威共摸了100次,其中20次摸到黑球,根据上述数据,可估计口袋中的白球大约有_____个.
14.“种瓜得瓜,种豆得豆”这一事件是
(填“必然事件”“不可能事件”“随机事件”
.
15.小明掷一枚硬币10次,有9次正面向上,当他掷第10次时,正面向上的概率是______.
16.一个布袋里装有10个只有颜色不同的球,这10个球中有m个红球,从布袋中摸出一个球,记下颜色后放回,搅匀,再摸出一个球,通过大量重复试验后发现,摸到红球的频率稳定在0.3左右,则m的值约为__________.
17.给出下列事件:
(1)某餐厅供应客饭,共准备2荤2素4种不同的品种,一顾客任选一种菜肴,且选中素菜;
(2)某一百件产品全部为正品,今从中选出一件次品;
(3)在1,2,3,4,5五条线路停靠的车站上,张老师等候到6路车;
(4)七人排成一排照相,甲、乙正好相邻;
(5)在有30个空位的电影院里,小红找到了一个空位,
请将事件的序号填写在横线上:
必然事件
,不可能事件
,不确定事件
.
18.在不透明的口袋中有若干个完全一样的红色小球,现放入10个仅颜色不同的白色小球,均匀混合后,有放回地随机摸取30次,有10次摸到白色小球,据此估计该口袋中原有红色小球个数为??????????.
19.在一个不透明的盒子中装有n个小球,它们除了颜色不同外,其余都相同,其中有4个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.大量重复上述试验后发现,摸到白球的频率稳定在0.4,那么可以推算出n的值大约是_______.
20.下面第一排表示十张扑克牌的不同情况,任意摸一张,请你将摸到红色扑克牌的可能性与对应的方框用线连起来.
21.一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外其余都相同.
(1)从袋中随机摸出一个球,记录其颜色,然后放回,大量重复该实验,发现摸到绿球的频率稳定于,求n的值;
(2)小明与小华进行摸球游戏,小明用摸出一球后,不放回,小华在摸出一球,若两次摸出的球颜色不同的则小明获胜,否则为小华获胜,试通过计算说明这个游戏是否公平.
22.下列事件中,哪些是必然事件?哪些是不可能事件?哪些是随机事件?
(1)太阳从西边落山;
(2)某人的体温是100
℃;
(3)a2+b2=0;
(4)某个等腰三角形中任意两个角都不相等;
(5)经过有信号灯的十字路口,遇见红灯.
23.甲乙两人玩“锤子、石头、剪子、布”游戏,他们在不透明的袋子中放入形状、大小均相同的22张卡片,其中写有“锤子”石头”、“剪子”、“布”的卡片张数分别为4、5、6、7.两人先后各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:
“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负.
(1)若甲先摸,则他摸出“剪子”的概率是多少?
(2)若甲先摸出了“剪子”,则乙获胜的概率是多少?
(3)若甲先摸,则他摸出哪种卡片获胜的可能性最大?
24.在一个不透明的盒子里装有红、黑两种颜色的球共60只,这些球除颜色外其余完全相同.为了估计红球和黑球的个数,七班的数学学习小组做了摸球实验.他们将球搅匀后,从盒子里随机摸出一个球记下颜色,再把球放回盒子中,多次重复上述过程,得到下表中的一组统计数据:
摸球的次数n
50
100
300
500
800
1000
2000
摸到红球的次数m
14
33
95
155
241
298
602
摸到红球的频率
(1)请估计:当次数n足够大时,摸到红球的频率将会接近______;精确到
(2)假如你去摸一次,则摸到红球的概率的估计值为______;
(3)试估算盒子里红球的数量为______个,黑球的数量为______
25.2019年女排世界杯中,中国女排以11站全胜且只丢3局的成绩成功卫冕本届世界杯冠军.某校七年级为了弘扬女排精神,组建了排球社团,通过测量同学们的身高(单位:cm),并绘制了如下两幅不完整的统计图,请结合图中提供的信息,解答下列问题.
(1)填空:样本容量为___,a=___;
(2)把频数分布直方图补充完整;
(3)若从该组随机抽取1名学生,估计这名学生身高低于165cm的概率.
26.在一个不透明的盒子里装有黑、白两种颜色的球共50个,这些球除颜色外其余完全相同.王颖做摸球试验,搅匀后,她从盒子里随机摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程,如表是试验中的一组统计数据:
摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
65
124
178
302
480
600
1800
摸到白球的频率
0.65
0.62
0.593
0.604
0.6
0.6
0.6
(1)请估计:当n很大时,摸到白球的频率将会接近
;(精确到0.1)
(2)若从盒子里随机摸出一个球,则摸到白球的概率的估计值为
;
(3)试估算盒子里黑、白两种颜色的球各有多少个?
参考答案
1.
A
2.
D
3.
B
4.
B
5.
C
6.
D
7.
B
8.
C
9.
C
10.
A
11.
9
12.
1/2
13.
16.
14.
必然事件 .
15.
1/2
16.
3
17.
(5) , (2)(3)
, (1)(4)
.
18.
20
19.
10
20.
21.
解:利用频率估计概率得到摸到绿球的概率为,
则,
解得;
画树状图为:
共有12种等可能的结果数,其中两次摸出的球的颜色不同的结果共有10?种,
所以两次摸出的球颜色不同的概率,
则小明胜的概率为、小华胜的概率为,
所以这个游戏不公平.
22.
(1)
“太阳从西边落山”是必然事件;(2)
“某人的体温是100
℃”是不可能事件;(3)
“a2+b2=0”是随机事件;(4)
“某个等腰三角形中任意两个角都不相等”是不可能事件;(5)
“经过有信号灯的十字路口,遇见红灯”是随机事件.
23.
(1)甲先摸,则他摸出“剪子”的概率.
(2)甲先摸出了“剪子”,不透明的袋子中有“锤子”石头”、“剪子”、“布”的卡片张数分别为4、5、5、7,
乙要获胜需要抽出“锤子”胜“石头”,乙获胜的概率.
(3)甲先摸出了“锤子”并且获胜,乙需要摸出”,“石头”或“剪子”,甲胜的概率
甲先摸出了“石头”并且获胜,乙需要摸出”“剪子”,甲胜的概率
甲先摸出了“剪子”并且获胜,乙需要摸出“布”,甲胜的概率
甲先摸出了“布”并且获胜,乙需要摸出“锤子”和“石头”,甲胜的概率,
其中最大,所以甲先摸出了“锤子”获胜的概率最大.
24.
解:当次数n足够大时,摸到红球的频率将会接近,故答案为;
摸到红球的概率的估计值为,故答案为;
估算盒子里红球的数量为个,黑球的个数为个,故答案为18;42.
25.
解:(1)15÷
=100,
所以样本容量为100;
B组的人数为100-15-35-15-5=30,
所以a%=
×100%=30%,则a=30;
故答案为100,30;
(2)补全频数分布直方图为:
(3)样本中身高低于165cm的人数为15+30+35=80,
样本中身高低于165cm的频率为,
所以估计从该地随机抽取1名学生,估计这名学生身高低于165cm的概率为.
26.
(1)0.6;(2)0.6;(3)盒子里黑颜色的球有20只,盒子白颜色的球有30只
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
