四川省泸州高中2019-2020学年高中物理教科版选修3-4:1.3简谐运动的图像和公式 质量检测(含解析)
文档属性
| 名称 | 四川省泸州高中2019-2020学年高中物理教科版选修3-4:1.3简谐运动的图像和公式 质量检测(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 271.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-07-08 00:00:00 | ||
图片预览




文档简介
1.3简谐运动的图像和公式
1.上端固定,下端挂盘的竖直弹簧,当在盘中放一砝码,使其在竖直方向上做振动砝码对底盘的压力最大处在
A.平衡位置
B.振动的最低点
C.振动的最高点
D.各处压力均相等
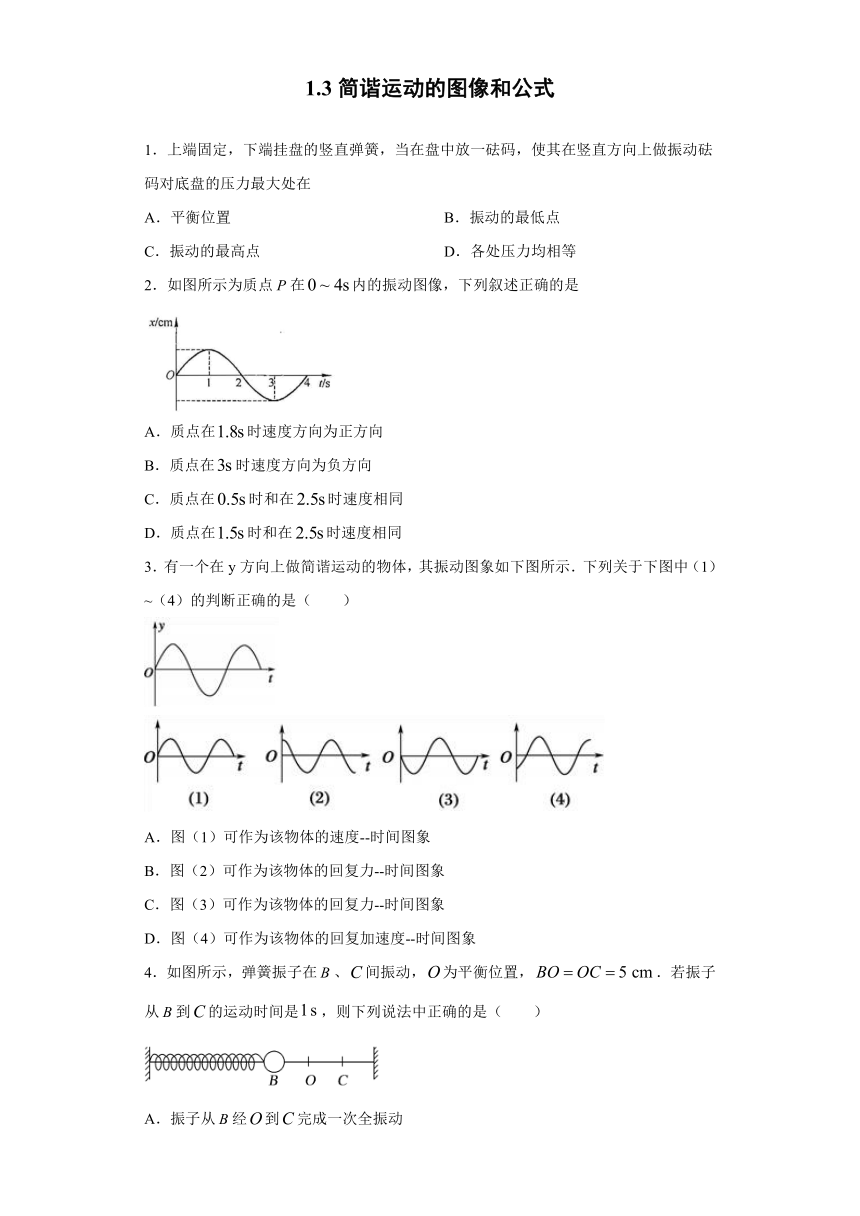
2.如图所示为质点P在内的振动图像,下列叙述正确的是
A.质点在时速度方向为正方向
B.质点在时速度方向为负方向
C.质点在时和在时速度相同
D.质点在时和在时速度相同
3.有一个在y方向上做简谐运动的物体,其振动图象如下图所示.下列关于下图中(1)~(4)的判断正确的是(
)
A.图(1)可作为该物体的速度--时间图象
B.图(2)可作为该物体的回复力--时间图象
C.图(3)可作为该物体的回复力--时间图象
D.图(4)可作为该物体的回复加速度--时间图象
4.如图所示,弹簧振子在、间振动,为平衡位置,.若振子从到的运动时间是,则下列说法中正确的是(
)
A.振子从经到完成一次全振动
B.振动周期是,振幅是
C.经过两次全振动,振子通过的路程是
D.从开始经过,振子通过的路程是
5.质点做简谐运动,其x—t关系如图,以x轴正向为速度v的正方向,该质点的v—t关系是(
)
A.
B.C.D.
6.一个质点做简谐振动的振动图像如图所示,则该质点在3.5s时的
A.速度为负,位移为正
B.速度为负,位移为负
C.速度为负,加速度为正
D.速度为正,加速度为负
7.如图甲所示,弹簧振子以O点为平衡位置,在A、B两点之间做简谐运动.取向右为正,振子的位移x随时间t的变化如图乙所示,则由图可知(
)
A.t=0.2s时,振子的加速度方向向左
B.t=0.6s时,振子的速度方向向右
C.t=0.4s到t=0.8s的时间内,振子的动能逐渐减小
D.t=0到t=2.4s的时间内,振子通过的路程是80cm
8.一弹簧振子沿x轴振动,振幅为.振子的平衡位置位于x轴上的O点.图中的a、b、c、d为四个不同的振动状态:黑点表示振子的位置,黑点上的箭头表示运动的方向.图中给出的①②③④四条振动图线,可用于表示振子的振动图像
A.若规定状态a时则图像为①
B.若规定状态b时则图像为②
C.若规定状态c时则图像为③
D.若规定状态d时则图像为④
9.一个质点做简谐运动的图象如下图所示,下述正确的是
A.质点振动频率为4
Hz
B.在10
s内质点经过的路程是20
cm
C.在5
s末,质点速度为零,加速度最大
D.在t=1.5
s和t=4.5
s两时刻质点位移大小相等
10.某质点做简谐运动,其位移随时间变化的关系式为(cm)
,则下列关于质点运动的说法中正确的是
(
)
A.质点做简谐运动的振幅为10cm
B.质点做简谐运动的周期为8s
C.在t=4s时质点的速度最大
D.在t=4s时质点的加速度最大
11.一质点的振动图像如图所示,根据图像确定:在哪些时间内质点振动的加速度指向正方向?在哪一时刻加速度方向指向负方向且加速度大小为最大?在哪些时间内振动速度方向为正方向?在哪一时刻速度指向负方向且速度大小为最大?
12.如图甲所示,轻弹簧上端固定,下端系一质量为m=1kg的小球,小球静止时弹簧伸长量为10cm.现使小球在竖直方向上做简谐运动,从小球在最低点释放时开始计时,小球相对平衡位置的位移,随时间t变化的规律如图乙所示,重力加速度g取10m/s2.
(1)写出小球相对平衡位置的位移随时间的变化关系式;
(2)求出小球在0~12.9s内运动的总路程和12.9s时刻的位置;
(3)小球运动到最高点时加速度的大小.
13.如图所示,将弹簧振子从平衡位置O向右拉开后4cm放手,让它做简谐运动,已知从放手到第一次回到平衡位置的时间为0.1s,求:
(1)弹簧振子的振幅、周期、频率.
(2)2s内完成全振动的次数.
(3)振子从开始运动经过2.5s的位移的大小.此刻正要向哪个方向做怎样的运动?
(4)振子经5s通过的路程.
(5)若将弹簧振子从平衡位置向右拉开6cm后释放,运动过程中的振幅、周期、频率变为多大?
参考答案
1.B
【解析】
砝码和托盘一起做简谐运动,当振动托盘运动到最高点时时,物体的加速度竖直向下,处于失重状态,砝码对托盘的正压力小于物体的重力;当振动平台向下运动过振动中心点时,物体的加速度为零,物体对托盘的正压力等于物体的重力;当振动托盘运动到最低点时,物体的加速度竖直向上,处于超重状态,物体对托盘的正压力大于物体的重力.因此,当托盘运动到最低点时,物体对托盘的正压力最大。故B正确,ACD错误;
故选:B
2.D
【解析】
A.根据振动图象“上坡上振,下坡下振”,质点在1.8s时速度向下,故A错误;
B.质点在3s时处于负向最大位移处,速度为零,故B错误;
C.根据振动图象“上坡上振,下坡下振”,质点在0.5s时速度方向向上,2.5s时速度方向向下,根据对称性,速度大小相等,方向相反,故C错误;
D.根据振动图象“上坡上振,下坡下振”,质点在0.5s时和2.5s时速度方向均向下,根据对称性,速度大小相等,故D正确;
故选择D;
3.C
【解析】
在简谐运动中,速度与位移是互余的关系,即位移为零,速度最大;位移最大,速度为零,则知速度与位移图象也互余,图(2)可以作为该物体的v-t图象.故A错误.由简谐运动特征F=-kx可知,回复力的图象与位移图象的相位相反,但也正弦曲线,则知图(2)不可作为该物体的F-t图象,图(3)可作为物体的F-t图象.故B错误,C正确;由a=-kx/m可知,加速度的图象与位移图象的相位相反,应为正弦曲线,则知图(4)不能作为该物体的a-t图象.故D错误.故选C.
4.D
【解析】
AB.振子从→→仅完成了半次全振动,所以周期
故错误;
C.振幅,振子在一次全振动中通过的路程为
所以两次全振动通过的路程为,故C错误;
D.的时间为,所以振子通过的路程为,故D正确.
5.B
【解析】
质点通过平衡位置时速度最大,由图知内,1s和3s两个时刻质点通过平衡位置,速度最大,根据图象切线的斜率等于速度,可知1s时刻速度为负向,3s时刻速度为正向,故具有最大正方向速度是3s.由加速度与位移的关系:
可知质点具有最大正方向加速度时有最大负向的位移,由图看出该时刻在2s,所以质点具有最大正方向加速度的时刻是2s,故选B.
6.D
【解析】
知道图像的意义,再结合简谐运动的模型分析求解。
【详解】
据图像可知,质点在时,质点的位移为正,且偏离平衡位置,所以位移、速度为正,根据:
可知,回复力与位移方向相反,即加速度也与位移方向相反,故D正确,ABC错误。
【点睛】
明确图像的意义是解题的关键,灵活与模型结合是解题的核心,知道位移、速度和加速度之间的变化关系。
7.A
【解析】
A.由图象乙知,t=0.2s时,振子远离平衡位置向右运动,位移增大,根据可知,回复力方向向左,则加速度方向向左,故A正确;
B.t=0.6s时,振子靠近平衡位置向左运动,所以振子的速度方向向左,故B错误;
C.t=0.4s到t=0.8s的时间内,振子向平衡位置运动,速度逐渐增大,振子的动能逐渐增大,故C错误;
D.t=0到t=2.4s的时间内,振子通过的路程是,故D错误;
8.AD
【解析】
A.仔细观察图(a)可知,a状态振子的位移为,且正向正方向运动图(b)中时位移为的图线只有①②,①表示振子正向正方向运动,②表示振子正向负方向运动,故选项A正确;
B.b状态振子的位移为,且正向负方向运动,图(b)中没有相符图线,选项B错;
C.c状态振子的位移为,且正向负方向运动,图(b)中的③虽然时位移为,但振子正向正方向运动,选项C错;
D.d状态振子位于负最大位移处,即将向正方向运动,符合图线④,选项D正确;
故选:AD;
9.BCD
【解析】
A:由振动图象,可得质点振动的周期,则质点振动频率.故A项错误.
B:一个周期内,简谐运动的质点经过的路程,10
s为2.5个周期,质点经过的路程为.故B项正确.
C:由图知,在5
s末,质点位移最大,加速度最大,速度为零.故C项正确.
D:由图知,在t=1.5
s和t=4.5
s两时刻质点位移相等.故D项正确.
10.BC
【解析】
A、由位移的表达式可知质点做简谐运动的振幅为5cm,故选项A错误;
B、由位移的表达式读出角频,则周期为,故选项B正确;
C、在时质点的位移,说明质点通过平衡位置,速度最大,故选项C正确;
D、在时质点通过平衡位置,加速度最小,故选项D错误。
11.到;0.1s;到,以及到时间内;
【解析】
质点做简谐运动时,加速度与位移关系为:
,
加速度方向与位移方向相反且始终指向平衡位置,加速度大小与位移大小成正比.而质点在某一时刻的速度方向则主要看经一小段时间后质点的位置变化.要使加速度向正方向,则位移应该向负方向,所以在到时间内质点振动的加速度指向正方向;
要使加速度向负方向且大小为最大,则位移应该为正方向且位移值为最大,所以在时加速度向负方向且加速度大小为最大;
在到时间内,以及到时间内振动速度方向为正方向;
在时速度向负方向且速度大小为最大;
12.(1)(2)215cm
;0(3)5m/s2
【解析】
(1)由振动图像可知:A=5cm,T=1.2s,则
小球相对平衡位置的位移随时间的变化关系式:
(2)12.9s=10T,则小球在0~12.9s内运动的总路程:43A=215cm;
12.9s时刻的位置:y=0;即在平衡位置.
(3)小球在平衡位置时弹簧伸长量10cm,则:
小球在最高点时,弹簧伸长5cm,则
解得
a=5m/s2
13.(1)4cm,0.4s,2.5Hz
(2)5
(3)位移为零,向左做加速度增大的减速运动
(4)2m
(5)振幅变为6cm,而周期与频率均不变
【解析】
(1)根据振幅的定义,可知振幅;由于一周期内有4个等时的运动阶段,从最大位移处向平衡位置运动的时间为,所以周期:
频率:
(2)因为:
所以内完成了5次全振动
(3)经过:
振子经整数周期恰好回到原来位置(即右侧最大位移处),再经振子正向左经过平衡位置,所以末振子的位移为零,向左做加速度增大的减速运动;
(4)由于振子在一个周期内运动的路程为4倍的振幅:
所以振子经过通过的路程为:
(5)由于振子振动的周期与振幅无关,所以振子的振幅变为,而周期与频率均不变。
1.上端固定,下端挂盘的竖直弹簧,当在盘中放一砝码,使其在竖直方向上做振动砝码对底盘的压力最大处在
A.平衡位置
B.振动的最低点
C.振动的最高点
D.各处压力均相等
2.如图所示为质点P在内的振动图像,下列叙述正确的是
A.质点在时速度方向为正方向
B.质点在时速度方向为负方向
C.质点在时和在时速度相同
D.质点在时和在时速度相同
3.有一个在y方向上做简谐运动的物体,其振动图象如下图所示.下列关于下图中(1)~(4)的判断正确的是(
)
A.图(1)可作为该物体的速度--时间图象
B.图(2)可作为该物体的回复力--时间图象
C.图(3)可作为该物体的回复力--时间图象
D.图(4)可作为该物体的回复加速度--时间图象
4.如图所示,弹簧振子在、间振动,为平衡位置,.若振子从到的运动时间是,则下列说法中正确的是(
)
A.振子从经到完成一次全振动
B.振动周期是,振幅是
C.经过两次全振动,振子通过的路程是
D.从开始经过,振子通过的路程是
5.质点做简谐运动,其x—t关系如图,以x轴正向为速度v的正方向,该质点的v—t关系是(
)
A.
B.C.D.
6.一个质点做简谐振动的振动图像如图所示,则该质点在3.5s时的
A.速度为负,位移为正
B.速度为负,位移为负
C.速度为负,加速度为正
D.速度为正,加速度为负
7.如图甲所示,弹簧振子以O点为平衡位置,在A、B两点之间做简谐运动.取向右为正,振子的位移x随时间t的变化如图乙所示,则由图可知(
)
A.t=0.2s时,振子的加速度方向向左
B.t=0.6s时,振子的速度方向向右
C.t=0.4s到t=0.8s的时间内,振子的动能逐渐减小
D.t=0到t=2.4s的时间内,振子通过的路程是80cm
8.一弹簧振子沿x轴振动,振幅为.振子的平衡位置位于x轴上的O点.图中的a、b、c、d为四个不同的振动状态:黑点表示振子的位置,黑点上的箭头表示运动的方向.图中给出的①②③④四条振动图线,可用于表示振子的振动图像
A.若规定状态a时则图像为①
B.若规定状态b时则图像为②
C.若规定状态c时则图像为③
D.若规定状态d时则图像为④
9.一个质点做简谐运动的图象如下图所示,下述正确的是
A.质点振动频率为4
Hz
B.在10
s内质点经过的路程是20
cm
C.在5
s末,质点速度为零,加速度最大
D.在t=1.5
s和t=4.5
s两时刻质点位移大小相等
10.某质点做简谐运动,其位移随时间变化的关系式为(cm)
,则下列关于质点运动的说法中正确的是
(
)
A.质点做简谐运动的振幅为10cm
B.质点做简谐运动的周期为8s
C.在t=4s时质点的速度最大
D.在t=4s时质点的加速度最大
11.一质点的振动图像如图所示,根据图像确定:在哪些时间内质点振动的加速度指向正方向?在哪一时刻加速度方向指向负方向且加速度大小为最大?在哪些时间内振动速度方向为正方向?在哪一时刻速度指向负方向且速度大小为最大?
12.如图甲所示,轻弹簧上端固定,下端系一质量为m=1kg的小球,小球静止时弹簧伸长量为10cm.现使小球在竖直方向上做简谐运动,从小球在最低点释放时开始计时,小球相对平衡位置的位移,随时间t变化的规律如图乙所示,重力加速度g取10m/s2.
(1)写出小球相对平衡位置的位移随时间的变化关系式;
(2)求出小球在0~12.9s内运动的总路程和12.9s时刻的位置;
(3)小球运动到最高点时加速度的大小.
13.如图所示,将弹簧振子从平衡位置O向右拉开后4cm放手,让它做简谐运动,已知从放手到第一次回到平衡位置的时间为0.1s,求:
(1)弹簧振子的振幅、周期、频率.
(2)2s内完成全振动的次数.
(3)振子从开始运动经过2.5s的位移的大小.此刻正要向哪个方向做怎样的运动?
(4)振子经5s通过的路程.
(5)若将弹簧振子从平衡位置向右拉开6cm后释放,运动过程中的振幅、周期、频率变为多大?
参考答案
1.B
【解析】
砝码和托盘一起做简谐运动,当振动托盘运动到最高点时时,物体的加速度竖直向下,处于失重状态,砝码对托盘的正压力小于物体的重力;当振动平台向下运动过振动中心点时,物体的加速度为零,物体对托盘的正压力等于物体的重力;当振动托盘运动到最低点时,物体的加速度竖直向上,处于超重状态,物体对托盘的正压力大于物体的重力.因此,当托盘运动到最低点时,物体对托盘的正压力最大。故B正确,ACD错误;
故选:B
2.D
【解析】
A.根据振动图象“上坡上振,下坡下振”,质点在1.8s时速度向下,故A错误;
B.质点在3s时处于负向最大位移处,速度为零,故B错误;
C.根据振动图象“上坡上振,下坡下振”,质点在0.5s时速度方向向上,2.5s时速度方向向下,根据对称性,速度大小相等,方向相反,故C错误;
D.根据振动图象“上坡上振,下坡下振”,质点在0.5s时和2.5s时速度方向均向下,根据对称性,速度大小相等,故D正确;
故选择D;
3.C
【解析】
在简谐运动中,速度与位移是互余的关系,即位移为零,速度最大;位移最大,速度为零,则知速度与位移图象也互余,图(2)可以作为该物体的v-t图象.故A错误.由简谐运动特征F=-kx可知,回复力的图象与位移图象的相位相反,但也正弦曲线,则知图(2)不可作为该物体的F-t图象,图(3)可作为物体的F-t图象.故B错误,C正确;由a=-kx/m可知,加速度的图象与位移图象的相位相反,应为正弦曲线,则知图(4)不能作为该物体的a-t图象.故D错误.故选C.
4.D
【解析】
AB.振子从→→仅完成了半次全振动,所以周期
故错误;
C.振幅,振子在一次全振动中通过的路程为
所以两次全振动通过的路程为,故C错误;
D.的时间为,所以振子通过的路程为,故D正确.
5.B
【解析】
质点通过平衡位置时速度最大,由图知内,1s和3s两个时刻质点通过平衡位置,速度最大,根据图象切线的斜率等于速度,可知1s时刻速度为负向,3s时刻速度为正向,故具有最大正方向速度是3s.由加速度与位移的关系:
可知质点具有最大正方向加速度时有最大负向的位移,由图看出该时刻在2s,所以质点具有最大正方向加速度的时刻是2s,故选B.
6.D
【解析】
知道图像的意义,再结合简谐运动的模型分析求解。
【详解】
据图像可知,质点在时,质点的位移为正,且偏离平衡位置,所以位移、速度为正,根据:
可知,回复力与位移方向相反,即加速度也与位移方向相反,故D正确,ABC错误。
【点睛】
明确图像的意义是解题的关键,灵活与模型结合是解题的核心,知道位移、速度和加速度之间的变化关系。
7.A
【解析】
A.由图象乙知,t=0.2s时,振子远离平衡位置向右运动,位移增大,根据可知,回复力方向向左,则加速度方向向左,故A正确;
B.t=0.6s时,振子靠近平衡位置向左运动,所以振子的速度方向向左,故B错误;
C.t=0.4s到t=0.8s的时间内,振子向平衡位置运动,速度逐渐增大,振子的动能逐渐增大,故C错误;
D.t=0到t=2.4s的时间内,振子通过的路程是,故D错误;
8.AD
【解析】
A.仔细观察图(a)可知,a状态振子的位移为,且正向正方向运动图(b)中时位移为的图线只有①②,①表示振子正向正方向运动,②表示振子正向负方向运动,故选项A正确;
B.b状态振子的位移为,且正向负方向运动,图(b)中没有相符图线,选项B错;
C.c状态振子的位移为,且正向负方向运动,图(b)中的③虽然时位移为,但振子正向正方向运动,选项C错;
D.d状态振子位于负最大位移处,即将向正方向运动,符合图线④,选项D正确;
故选:AD;
9.BCD
【解析】
A:由振动图象,可得质点振动的周期,则质点振动频率.故A项错误.
B:一个周期内,简谐运动的质点经过的路程,10
s为2.5个周期,质点经过的路程为.故B项正确.
C:由图知,在5
s末,质点位移最大,加速度最大,速度为零.故C项正确.
D:由图知,在t=1.5
s和t=4.5
s两时刻质点位移相等.故D项正确.
10.BC
【解析】
A、由位移的表达式可知质点做简谐运动的振幅为5cm,故选项A错误;
B、由位移的表达式读出角频,则周期为,故选项B正确;
C、在时质点的位移,说明质点通过平衡位置,速度最大,故选项C正确;
D、在时质点通过平衡位置,加速度最小,故选项D错误。
11.到;0.1s;到,以及到时间内;
【解析】
质点做简谐运动时,加速度与位移关系为:
,
加速度方向与位移方向相反且始终指向平衡位置,加速度大小与位移大小成正比.而质点在某一时刻的速度方向则主要看经一小段时间后质点的位置变化.要使加速度向正方向,则位移应该向负方向,所以在到时间内质点振动的加速度指向正方向;
要使加速度向负方向且大小为最大,则位移应该为正方向且位移值为最大,所以在时加速度向负方向且加速度大小为最大;
在到时间内,以及到时间内振动速度方向为正方向;
在时速度向负方向且速度大小为最大;
12.(1)(2)215cm
;0(3)5m/s2
【解析】
(1)由振动图像可知:A=5cm,T=1.2s,则
小球相对平衡位置的位移随时间的变化关系式:
(2)12.9s=10T,则小球在0~12.9s内运动的总路程:43A=215cm;
12.9s时刻的位置:y=0;即在平衡位置.
(3)小球在平衡位置时弹簧伸长量10cm,则:
小球在最高点时,弹簧伸长5cm,则
解得
a=5m/s2
13.(1)4cm,0.4s,2.5Hz
(2)5
(3)位移为零,向左做加速度增大的减速运动
(4)2m
(5)振幅变为6cm,而周期与频率均不变
【解析】
(1)根据振幅的定义,可知振幅;由于一周期内有4个等时的运动阶段,从最大位移处向平衡位置运动的时间为,所以周期:
频率:
(2)因为:
所以内完成了5次全振动
(3)经过:
振子经整数周期恰好回到原来位置(即右侧最大位移处),再经振子正向左经过平衡位置,所以末振子的位移为零,向左做加速度增大的减速运动;
(4)由于振子在一个周期内运动的路程为4倍的振幅:
所以振子经过通过的路程为:
(5)由于振子振动的周期与振幅无关,所以振子的振幅变为,而周期与频率均不变。
同课章节目录
- 第一章 机械振动
- 1 简谐运动
- 2 单摆
- 3 简谐运动的图像和公式
- 4 阻尼振动 受迫振动
- 5 实验探究:用单摆测定重力加速度
- 第二章 机械波
- 1 机械波的形成和传播
- 2 横波的图像
- 3 波的频率和波速
- 4 惠更新原理 波的反射与折射
- 5 波的干射 衍射
- 6 多普勒效应
- 第三章 电磁振荡 电磁波
- 1 电磁振荡
- 2 电磁场和电磁波
- 3 电磁波谱 电磁波的应用
- 4 无线电波的发射、传播和接收
- 第四章 光的折射
- 1 光的折射定律
- 2 实验探究:测定玻璃的折射率
- 3 光的全反射
- 第五章 光的波动性
- 1 光的干涉
- 2 实验探究:用双缝干涉油光的波长
- 3 光的衍射与偏振
- 4 激光
- 第六章 相对论
- 1 经典时空观
- 2 狭义对相对论的两个基本假设
- 3 相对论时空观
- 4 相对论的速度变换定律 质量和能量的关系
- 5 广义相对论
