苏教版高中数学必修二 1.2.3直线与平面的位置关系 同步练习(含答案解析)
文档属性
| 名称 | 苏教版高中数学必修二 1.2.3直线与平面的位置关系 同步练习(含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 677.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-10 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
苏教版高中数学必修二1.2.3直线与平面的位置关系
一、单选题
1.在下列命题中,不是公理的是(??
)
A.?经过两条相交直线有且只有一个平面
B.?平行于同一直线的两条直线互相平行
C.?如果一条直线上的两点在一个平面内,那么这条直线在此平面内
D.?如果两个不重合的平面有一个公共点,那么他们有且只有一条过该点的公共直线
2.已知两条互不重合的直线m,n,两个不同的平面α,β,下列命题中正确的是( )
A.?若m∥α,n∥β,且m∥n,则α∥β???????????????????????B.?若m⊥α,n∥β,且m⊥n,则α⊥β
C.?若m⊥α,n∥β,且m∥n,则α∥β??????????????????????D.?若m⊥α,n⊥β,且m⊥n,则α⊥β
3.与同一平面平行的两条直线(
??)
A.?平行??????????????????????????????B.?相交??????????????????????????????C.?异面??????????????????????????????D.?平行、相交或异面
4.关于直线m,n与平面
,
有以下四个命题:
①若且
,
则m//n;???②若且
,
则;
③若且
,
则;??④若且
,
则m//n;
其中真命题的序号是(??????)
A.?①②?????????????????????????????????????B.?③④?????????????????????????????????????C.?①④?????????????????????????????????????D.?②③
5.下面四个说法(其中A、B表示点,a表示直线,α表示平面):
①∵A?α
,
B?α
,
∴AB?α;
②∵A∈α
,
B?α
,
∴AB?α;
③∵A?a
,
a?α
,
∴A?α;
④∵A∈a
,
a?α
,
∴A∈α.
其中表述方式和推理都正确的命题的序号是
(
??)
A.?①④???????????????????????????????????????B.?②③???????????????????????????????????????C.?④???????????????????????????????????????D.?③
6.α是一个平面,m,n是两条直线,A是一个点,若m?α,n?α,且A∈m,A∈α,则m,n的位置关系不可能是(??
)
A.?垂直?????????????????????????????????????B.?相交?????????????????????????????????????C.?异面?????????????????????????????????????D.?平行
7.下列命题中:
①若A∈α,B∈α,C∈AB,则C∈α;
②若α∩β=l,b?α,c?β,b∩c=A,则A∈l;
③A,B,C∈α,A,B,C∈β且A,B,C不共线,则α与β重合;
④任意三点不共线的四点必共面.
其中真命题的个数是( )
A.?0???????????????????????????????????????????B.?1???????????????????????????????????????????C.?2???????????????????????????????????????????D.?3
8.在空间中,a、b是两条不同的直线,α、β是两个不同的平面,下列说法正确的是(??
)
A.?若a∥α,b∥a,则b∥α????????????????????????????????????????B.?若a∥α,b∥α,a?β,b?β,则β∥α
C.?若α∥β,b∥α,则b∥β???????????????????????????????????????D.?若α∥β,a?α,则a∥β
9.空间中垂直于同一条直线的两条直线的位置关系是(????
)
A.?平行????????????????????????????????B.?相交????????????????????????????????C.?异面????????????????????????????????D.?以上都有可能
10.在正四棱柱
中,顶点
到对角线
和到平面
的距离分别为
和
,则下列命题中正确的是(
)
A.?若侧棱的长小于底面的变长,则
的取值范围为
??????
B.?若侧棱的长小于底面的变长,则
的取值范围为
C.?若侧棱的长大于底面的变长,则
的取值范围为
??????????
D.?若侧棱的长大于底面的变长,则
的取值范围为
二、填空题
11.已知α、β是不同的平面,l、m、n是不同的直线,P为空间中一点.若α∩β=l,m?α、n?β、m∩n=P,则点P与直线l的位置关系用符号表示为________.
12.在正方体ABCD﹣A1B1C1D1中,异面直线A1B与AC所成的角是________
13.有以下三个命题:
①平面外的一条直线与这个平面最多有一个公共点;
②直线l在平面α内,可以用符号“l∈α”表示;
③已知平面α与β不重合,若平面α内的一条直线a与平面β内的一条直线b相交,则α与β相交.其中真命题的序号是________.
14.给出下列四个命题:
①三点确定一个平面;
②三条两两相交的直线确定一个平面;
③在空间上,与不共面四点A,B,C,D距离相等的平面恰有7个;
④两个相交平面把空间分成四个区域.
其中真命题的序号是________?(写出所有真命题的序号).
三、解答题
15.如图,已知
平面
,且平面
平面
,求证
16.如图,已知ABCD是空间四边形,AB=AD,CB=CD,求证:BD⊥AC.
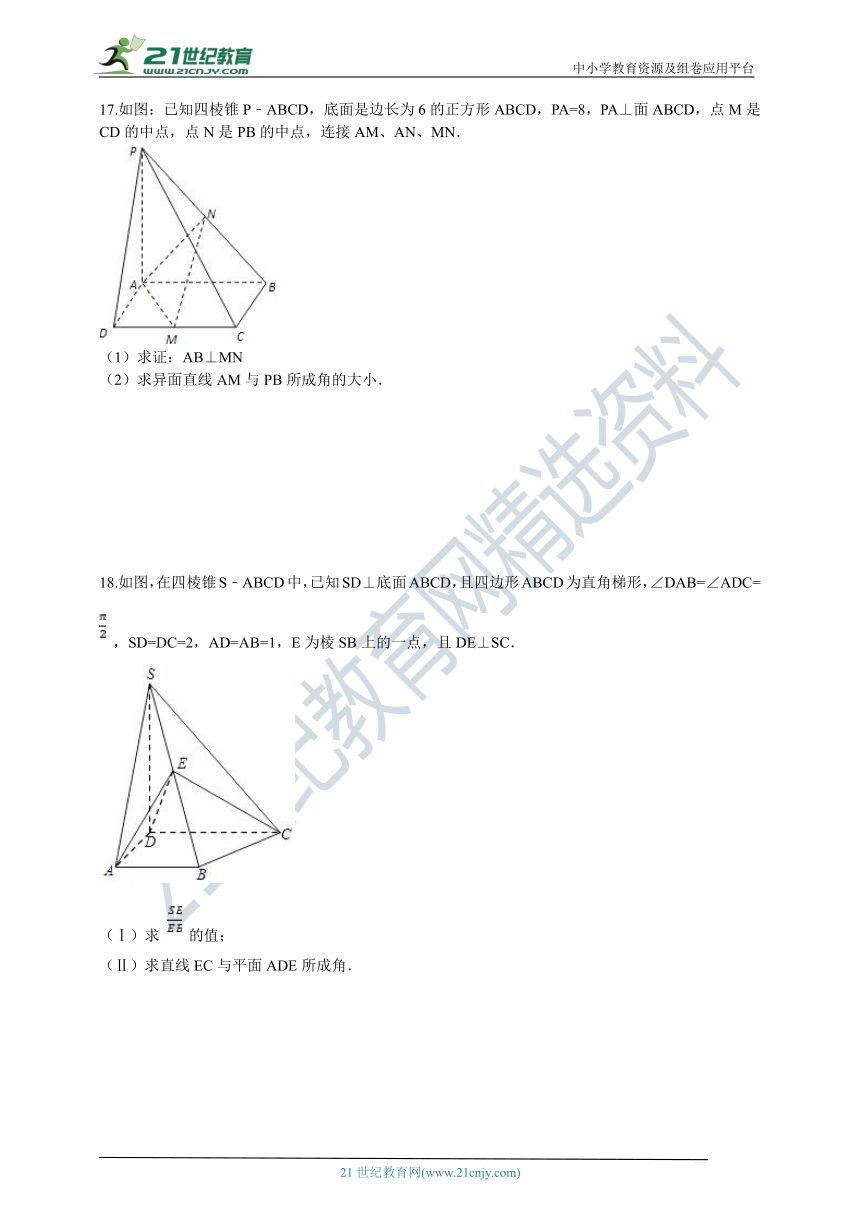
17.如图:已知四棱锥P﹣ABCD,底面是边长为6的正方形ABCD,PA=8,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM、AN、MN.
(1)求证:AB⊥MN
(2)求异面直线AM与PB所成角的大小.
18.如图,在四棱锥S﹣ABCD中,已知SD⊥底面ABCD,且四边形ABCD为直角梯形,∠DAB=∠ADC=
,SD=DC=2,AD=AB=1,E为棱SB上的一点,且DE⊥SC.
(Ⅰ)求
的值;
(Ⅱ)求直线EC与平面ADE所成角.
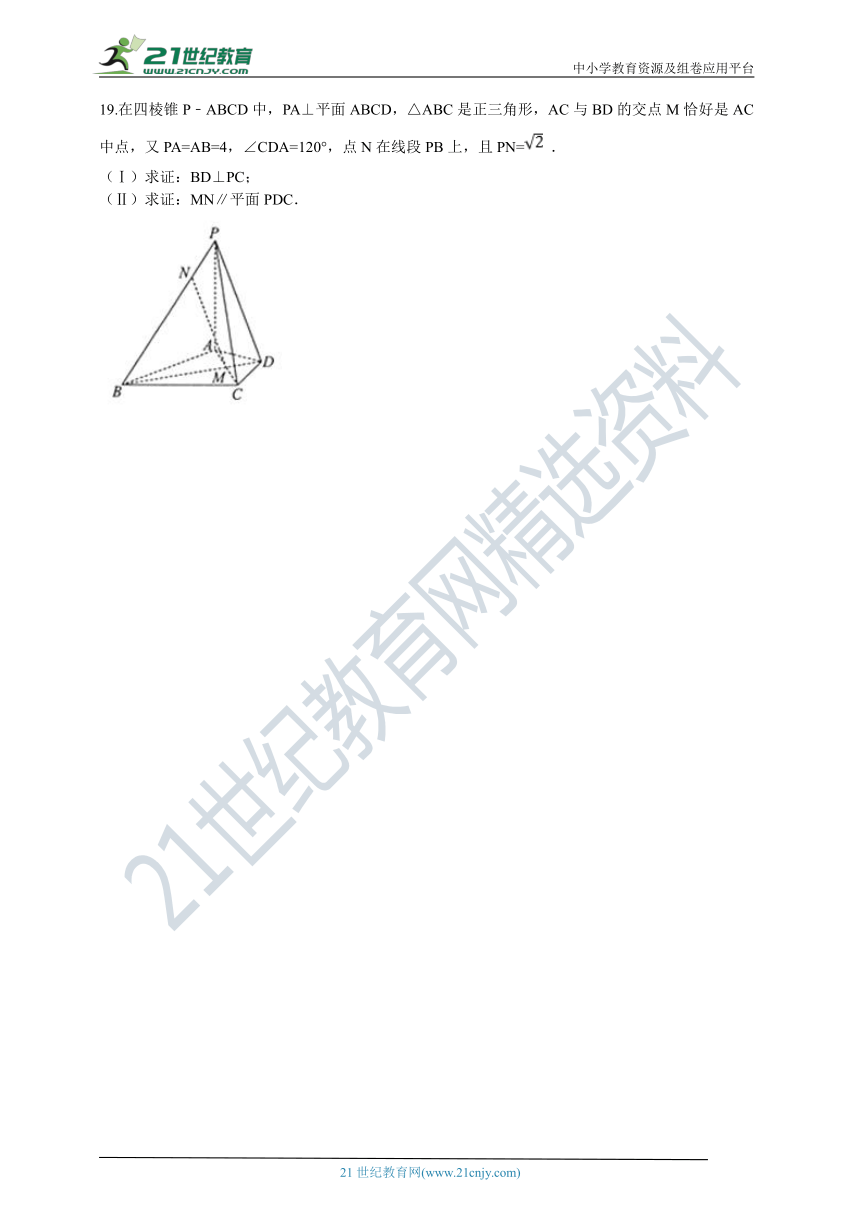
19.在四棱锥P﹣ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=
.
(Ⅰ)求证:BD⊥PC;
(Ⅱ)求证:MN∥平面PDC.
答案解析部分
一、单选题
1.【答案】
A
【解析】解:对于A,经过两条相交直线有且只有一个平面,是公理2的推理,不是公理;
对于B,平行于同一直线的两条直线互相平行,是平行公理;
对于C,如果一条直线上的两点在一个平面内,那么这条直线在此平面内,是公理1;
对于D,如果两个不重合的平面有一个公共点,那么他们有且只有一条过该点的公共直线,是公理3.
故选:A.
【分析】根据空间中平面的基本公理与推论,对选项中的命题进行分析、判断即可.
2.【答案】
D
【解析】解:若m∥α,n∥β,且m∥n,则α与β平行或相交,故A错误
若m⊥α,n∥β,且m⊥n,则α与β平行或相交,所以B错误.
若m⊥α,m∥n,则n⊥α,又由n∥β,且则α⊥β,故C错误;
若m⊥α,n⊥β,且m⊥n,则α⊥β,故D正确
故选D
【分析】根据线面平行及线线平行的几何特征,结合面面平行的判定方法,可以判断A的真假;
由线面垂直的几何特征及面面垂直的判定方法可以判断B的真假,
根据线面垂直及面面平行的几何特征,可以判断C的真假,
根据线面垂直,面面垂直及线线垂直之间的互相转化,可以判断D的真假,进而得到答案.
3.【答案】
D
【解析】与同一平面平行的两条直线的位置关系有三种情况,即平行、相交或异面。
故答案为:D。
【分析】本题考察的是空间想象能力,结合绘制图像,即可得出答案。
4.【答案】
D
【解析】由题意两条直线m,n与两个平面α,β由于m∥α,n∥β且α∥β,不能确定两条直线的位置关系,故若m∥α,n∥β且α∥β,则m⊥n是假命题;由于若m⊥α,n⊥β且α⊥β,不能确定两条直线的位置关系,故若m⊥α,n⊥β且α⊥β,则m∥n是假命题;由于m∥α,n⊥β且α⊥β不能确定两条直线的位置关系,故若m∥α,n⊥β且α⊥β,则m∥n是假命题;由于n∥β且α∥β可得出n?α或n∥α,又m⊥α可得出m⊥n故若m⊥α,n∥β且α∥β,则m⊥n是真命题.综上知,D选项正确,故选D
【分析】由题意,不同的两条直线m,n与两个平面α,β,A,D两个选项可由线线垂直的条件作作出判断,C,B两个选项可由线线平行的条件作出判断,得出正确选项本题的考点是间中直线一直线之间的位置关系,考查了线线平行与线线垂直的条件,解题的关键是理解题意,有着较强的空间立体感知能力,本题考查了空间想像能力,推理判断的能力,是高考中常见题型,其特点是涉及到的知识点多,知识容量大,因此备受高考命题者青睐
5.【答案】
C
【解析】①错,应写为A∈α
,
B∈α;②错,应写为AB?α;③错,推理错误,有可能A∈α;④推理与表述都正确.选C.
【分析】根据空间中点、线、面的位置关系可得结果。注意符号的正确使用。
6.【答案】D
【解析】解:∵α是一个平面,m,n是两条直线,A是一个点,
m?α,n?α,
∴n在平面a上,m与平面a相交
∵A∈m.A∈a
∴A是M和平面a相交的点
∴m和n
异面或相交,一定不平行.
故选:D.
【分析】由已知得n在平面a上,m与平面a相交,A是M和平面a相交的点,从而m和n
异面或相交,一定不平行.
7.【答案】
D
【解析】解:对于①,若A∈α,B∈α,C∈AB,根据平面的基本性质得到C∈α;故意正确;
对于②,若α∩β=l,b?α,c?β,b∩c=A,根据平面的基本性质容易得到A同时在两个平面内,即A∈l;故②正确;
对于③,A,B,C∈α,A,B,C∈β且A,B,C不共线,根据不共线的三点确定一个平面,容易得到α与β重合;故③正确;
对于④,任意三点不共线的四点不一定共面.比如空间四面体;故④错误;
故选D.
【分析】利用平面的基本性质对四个命题分别分析解答.
8.【答案】D
【解析】解:对于A,若a∥α,b∥a,说明b与平面α的平行线a平行,b可能在平面α内,它们的位置关系应该是平行或直线在平面内,故A错;
对于B,若a∥α,b∥α,a?β,b?β,说明在平面α和平面β内各有一条直线与另一个平面平行,但是条件并没有指明平面α、β的位置关系,平面α、β也可能相交,故不一定α∥β,故B错;
对于C,若α∥β,b∥α,说明直线b∥β或b?β,故不一定b∥β,故C错;
对于D,若α∥β,a?α,根据面面平行的性质:两个平行平面中的一个平面的直线必定平行于另一个平面,知a∥β,故D正确.
故选D.
【分析】对于A、B、C、D各项逐个加以分析:根据线面平行的判定及性质得到A错误;根据面面平行的判定得到B错误;根据面面平行的性质得到C错误;根据面面平行的性质,可得D正确.
9.【答案】
D
【解析】【分析】结合公理及正方体模型可以判断:A,B,C均有可能,可以利用反证法证明结论,也可以从具体的实物模型中去寻找反例证明.
【解答】如图,在正方体AC1中,
∵A1A⊥平面ABCD,∴A1A⊥AD,A1A⊥BC,
又∵AD∥BC,∴选项A有可能;
∵A1A⊥平面ABCD,∴A1A⊥AD,A1A⊥AB
,
又∵AD∩AB=A,∴选项B有可能;
∵A1A⊥平面ABCD,A1A⊥平面A1B1C1D1
,
∴A1A⊥AC,A1A⊥A1D1
,
又∵AC与A1D1不在同一平面内,∴选项C有可能.
故选D.
10.【答案】
C
【解析】设侧棱长是
,
底面的变长是
,点
到对角线
的距离
即为直角三角形
斜边
上的高,
,点
到平面
的距离分别
即为直角三角形
斜边
上的高,
若侧棱的长小于底面的变长,
即
,
A,B错误;
若侧棱的长大于底面的变长,
即
,
故答案为:C
【分析】设侧棱长是
b,
底面的变长是
a,点
B1到对角线
BD1的距离
h
即为直角三角形
△B1BD1
斜边
BD1上的高,得到点
B1到平面
A1BCD1的距离分别
d
即为直角三角形
△B1BA斜边B1A
上的高,得到,若侧棱的长小于底面的变长时,可判断A、B错误,若侧棱的长大于底面的变长,可判断C是正确的。
二、填空题
11.【答案】P∈l
【解析】因为m?α
,
n?β
,
m∩n=P
,
所以P∈α且P∈β.又α∈β=l
,
所以点P在直线l上,所以P∈l.【分析】根据平面的性质2,得到点P在平面和平面的交线上。
12.【答案】60°
【解析】连结BC1、A1C1
,
∵在正方体ABCD﹣A1B1C1D1中,A1A平行且等于C1C,
∴四边形AA1C1C为平行四边形,可得A1C1∥AC,
因此∠BA1C1(或其补角)是异面直线A1B与AC所成的角,设正方体的棱长为a,则△A1B1C中A1B=BC1=C1A1=a,
∴△A1B1C是等边三角形,可得∠BA1C1=60°,
即异面直线A1B与AC所成的角等于60°.
故答案为:60°.
【分析】连结BC1、A1C1
,
由正方体的性质可得四边形AA1C1C为平行四边形,从而A1C1∥AC,∠BA1C1是异面直线A1B与AC所成的角.然后求解异面直线A1B与AC所成的角.
13.【答案】①③
【解析】若直线与平面有两个公共点,则这条直线一定在这个平面内,故①正确;直线l在平面α内用符号“?”表示,即l?α,②错误;由a与b相交,说明两个平面有公共点,因此一定相交,故③正确.故答案为:①③
【分析】由平面的基本性质对各命题进行判断.
14.【答案】③④
【解析】解:对于①,不在同一直线上的三点确定一个平面,∴①错误;
对于②,不共点的三条两两相交的直线确定一个平面,∴②错误;
对于③,空间四点A、B、C、D不共面时,则四点构成一个三棱锥,如图:
当平面一侧有一点,另一侧有三点时,令截面与四棱锥的四个面之一平行,第四个顶点到这个截面的距离与其相对的面到此截面的距离相等,这样的平面有4个,
当平面一侧有两点,另一侧有两点时,即过相对棱的异面直线公垂线段的中点,且和两条相对棱平行的平面,满足条件.因三棱锥的相对棱有三对,则此时满足条件的平面个数是3个,
所以满足条件的平面恰有7个,③正确;
对于④,两个相交平面把空间分成四个区域是真命题,∴④正确.
综上,正确的命题序号是③④.
故答案为:③④.
【分析】①根据平面的公理“三点定面”即可判断命题错误;
②根据三条两两相交的直线可能不共面,即可判断命题错误;
③根据空间四点不共面时,四点构成一个三棱锥,讨论平面一侧有一点,另一侧有三点时,和平面一侧有两点,另一侧有两点时,满足条件的平面数是多少即可;
④根据实际情况即可得出结论正确.
三、解答题
15.【答案】
证明:如图所示,作
,
因为平面
平面
,
是平面
与平面
的交线,
,
所以
平面
,
,
因为
平面
,所以
,
因为
,所以
平面
,
。
【解析】【分析】本题首先可以作
,然后根据平面
平面
即可得出
,再然后通过
平面
即可得出
,最后通过线面垂直的相关证明以及性质即可得出结果。
16.【答案】
证明:取BD的中点O,连接AO,CO.
∵AB=AD,∴AO⊥BD,
∵CB=CD,∴CO⊥BD,
又AO∩CO=O,
∴BD⊥平面ACO,
AC?平面ACO,
∴BD⊥AC.
【解析】【分析】取BD的中点O,连接AO,CO.由等腰三角形的三线合一,得到AO⊥BD,CO⊥BD,再由线面垂直的判定定理得到BD⊥平面ACO,运用线面垂直的性质即可得证.
17.【答案】
(1)解:分别取AB,PA中点E,F,连接CE,EF,CF,NE,ME.
∵E是AB中点,点N是PB的中点,
∴
∵PA⊥面ABCD,
∴NE⊥面ABCD,NE⊥AB.
又∵MN∥BC,∴MN⊥AB.
所以:AB⊥MN,
得证.
(2)解:∵E是AB中点,F是PA中点E,N是PB的中点,点M是CD的中点
∴AM
CE,FE
.
所以:异面直线AM与PB所成角的大小即相交直线CF与EF所成角的大小
在△CEF中:EC=MA=
=
,FE=
,FC=
.
利用余弦定理:
cos∠FEC=
∵cos∠FEC<0,
∴∠FEC是钝角.
所以异面直线AM与PB所成角的大小为π﹣
【解析】【分析】(1)由题意,证明线线垂直,利用“三垂线定理或三垂线定理的逆定理”即可解决.(2)异面直线所成角,首先要构造出这两条异面直线的平行线相交的角,即为异面直线所成角.由题意,分别取AB,PA中点E,F,连接CE,EF,CF,所以异面直线AM与PB所成角的大小即相交直线CF与EF所成角的大小.
18.【答案】
解:(Ⅰ)以D为原点,DA,DC,DS为正交基底建立如图所示的空间直角坐标系D﹣xyz,
则各点的坐标为A(1,0,0),B(1,1,0),C(0,2,0),S(0,0,2).
=(0,2,﹣2),
=(1,1,﹣2),令
,
则
=(λ,λ,﹣2λ),
=
=(0,0,2)+(λ,λ,﹣2λ)=(λ,λ,2﹣2λ),
∵DE⊥SC,∴
=0,即2λ﹣2(2﹣2λ)=0,故
.
∴
=2
(Ⅱ)由(Ⅰ)知,
=(
),
=(﹣
),
设
=(x,y,z)为平面ADE的法向量,
则
,令y=1,得
=(0,1,﹣1)为平面ADE的法向量,
于是cos<
>=
=
=
,
∴直线EC与平面ADE所成角为
【解析】【分析】(Ⅰ)以D为原点,DA,DC,DS为正交基底建立如图所示的空间直角坐标系D﹣xyz,利用向量法能求出
的值.(Ⅱ)分别求出平面ADE的法向量和
,利用向量法能求出直线EC与平面ADE所成角.
19.【答案】证明:(I)∵△ABC是正三角形,M是AC中点,
∴BM⊥AC,即BD⊥AC.
又∵PA⊥平面ABCD,∴PA⊥BD.
又PA∩AC=A,∴BD⊥平面PAC.
∴BD⊥PC.
(Ⅱ)在正△ABC中,BM=2.
在△ACD中,
∵M为AC中点,DM⊥AC,∴AD=CD.
∠ADC=120°,
∴DM=,
∴=.
在等腰直角△PAB中,PA=AB=4,PB=4,
∴=,
∴,
∴MN∥PD.
又MN?平面PDC,PD?平面PDC,
∴MN∥平面PDC.
【解析】【分析】(Ⅰ)由正三角形的性质可得BD⊥AC,利用线面垂直的性质可知PA⊥BD,再利用线面垂直的判定定理即可证明BD⊥PC;
(Ⅱ)利用已知条件分别求出BM、MD、PB,得到
,
即可得到MN∥PD,再利用线面平行的判定定理即可证明
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
苏教版高中数学必修二1.2.3直线与平面的位置关系
一、单选题
1.在下列命题中,不是公理的是(??
)
A.?经过两条相交直线有且只有一个平面
B.?平行于同一直线的两条直线互相平行
C.?如果一条直线上的两点在一个平面内,那么这条直线在此平面内
D.?如果两个不重合的平面有一个公共点,那么他们有且只有一条过该点的公共直线
2.已知两条互不重合的直线m,n,两个不同的平面α,β,下列命题中正确的是( )
A.?若m∥α,n∥β,且m∥n,则α∥β???????????????????????B.?若m⊥α,n∥β,且m⊥n,则α⊥β
C.?若m⊥α,n∥β,且m∥n,则α∥β??????????????????????D.?若m⊥α,n⊥β,且m⊥n,则α⊥β
3.与同一平面平行的两条直线(
??)
A.?平行??????????????????????????????B.?相交??????????????????????????????C.?异面??????????????????????????????D.?平行、相交或异面
4.关于直线m,n与平面
,
有以下四个命题:
①若且
,
则m//n;???②若且
,
则;
③若且
,
则;??④若且
,
则m//n;
其中真命题的序号是(??????)
A.?①②?????????????????????????????????????B.?③④?????????????????????????????????????C.?①④?????????????????????????????????????D.?②③
5.下面四个说法(其中A、B表示点,a表示直线,α表示平面):
①∵A?α
,
B?α
,
∴AB?α;
②∵A∈α
,
B?α
,
∴AB?α;
③∵A?a
,
a?α
,
∴A?α;
④∵A∈a
,
a?α
,
∴A∈α.
其中表述方式和推理都正确的命题的序号是
(
??)
A.?①④???????????????????????????????????????B.?②③???????????????????????????????????????C.?④???????????????????????????????????????D.?③
6.α是一个平面,m,n是两条直线,A是一个点,若m?α,n?α,且A∈m,A∈α,则m,n的位置关系不可能是(??
)
A.?垂直?????????????????????????????????????B.?相交?????????????????????????????????????C.?异面?????????????????????????????????????D.?平行
7.下列命题中:
①若A∈α,B∈α,C∈AB,则C∈α;
②若α∩β=l,b?α,c?β,b∩c=A,则A∈l;
③A,B,C∈α,A,B,C∈β且A,B,C不共线,则α与β重合;
④任意三点不共线的四点必共面.
其中真命题的个数是( )
A.?0???????????????????????????????????????????B.?1???????????????????????????????????????????C.?2???????????????????????????????????????????D.?3
8.在空间中,a、b是两条不同的直线,α、β是两个不同的平面,下列说法正确的是(??
)
A.?若a∥α,b∥a,则b∥α????????????????????????????????????????B.?若a∥α,b∥α,a?β,b?β,则β∥α
C.?若α∥β,b∥α,则b∥β???????????????????????????????????????D.?若α∥β,a?α,则a∥β
9.空间中垂直于同一条直线的两条直线的位置关系是(????
)
A.?平行????????????????????????????????B.?相交????????????????????????????????C.?异面????????????????????????????????D.?以上都有可能
10.在正四棱柱
中,顶点
到对角线
和到平面
的距离分别为
和
,则下列命题中正确的是(
)
A.?若侧棱的长小于底面的变长,则
的取值范围为
??????
B.?若侧棱的长小于底面的变长,则
的取值范围为
C.?若侧棱的长大于底面的变长,则
的取值范围为
??????????
D.?若侧棱的长大于底面的变长,则
的取值范围为
二、填空题
11.已知α、β是不同的平面,l、m、n是不同的直线,P为空间中一点.若α∩β=l,m?α、n?β、m∩n=P,则点P与直线l的位置关系用符号表示为________.
12.在正方体ABCD﹣A1B1C1D1中,异面直线A1B与AC所成的角是________
13.有以下三个命题:
①平面外的一条直线与这个平面最多有一个公共点;
②直线l在平面α内,可以用符号“l∈α”表示;
③已知平面α与β不重合,若平面α内的一条直线a与平面β内的一条直线b相交,则α与β相交.其中真命题的序号是________.
14.给出下列四个命题:
①三点确定一个平面;
②三条两两相交的直线确定一个平面;
③在空间上,与不共面四点A,B,C,D距离相等的平面恰有7个;
④两个相交平面把空间分成四个区域.
其中真命题的序号是________?(写出所有真命题的序号).
三、解答题
15.如图,已知
平面
,且平面
平面
,求证
16.如图,已知ABCD是空间四边形,AB=AD,CB=CD,求证:BD⊥AC.
17.如图:已知四棱锥P﹣ABCD,底面是边长为6的正方形ABCD,PA=8,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM、AN、MN.
(1)求证:AB⊥MN
(2)求异面直线AM与PB所成角的大小.
18.如图,在四棱锥S﹣ABCD中,已知SD⊥底面ABCD,且四边形ABCD为直角梯形,∠DAB=∠ADC=
,SD=DC=2,AD=AB=1,E为棱SB上的一点,且DE⊥SC.
(Ⅰ)求
的值;
(Ⅱ)求直线EC与平面ADE所成角.
19.在四棱锥P﹣ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=
.
(Ⅰ)求证:BD⊥PC;
(Ⅱ)求证:MN∥平面PDC.
答案解析部分
一、单选题
1.【答案】
A
【解析】解:对于A,经过两条相交直线有且只有一个平面,是公理2的推理,不是公理;
对于B,平行于同一直线的两条直线互相平行,是平行公理;
对于C,如果一条直线上的两点在一个平面内,那么这条直线在此平面内,是公理1;
对于D,如果两个不重合的平面有一个公共点,那么他们有且只有一条过该点的公共直线,是公理3.
故选:A.
【分析】根据空间中平面的基本公理与推论,对选项中的命题进行分析、判断即可.
2.【答案】
D
【解析】解:若m∥α,n∥β,且m∥n,则α与β平行或相交,故A错误
若m⊥α,n∥β,且m⊥n,则α与β平行或相交,所以B错误.
若m⊥α,m∥n,则n⊥α,又由n∥β,且则α⊥β,故C错误;
若m⊥α,n⊥β,且m⊥n,则α⊥β,故D正确
故选D
【分析】根据线面平行及线线平行的几何特征,结合面面平行的判定方法,可以判断A的真假;
由线面垂直的几何特征及面面垂直的判定方法可以判断B的真假,
根据线面垂直及面面平行的几何特征,可以判断C的真假,
根据线面垂直,面面垂直及线线垂直之间的互相转化,可以判断D的真假,进而得到答案.
3.【答案】
D
【解析】与同一平面平行的两条直线的位置关系有三种情况,即平行、相交或异面。
故答案为:D。
【分析】本题考察的是空间想象能力,结合绘制图像,即可得出答案。
4.【答案】
D
【解析】由题意两条直线m,n与两个平面α,β由于m∥α,n∥β且α∥β,不能确定两条直线的位置关系,故若m∥α,n∥β且α∥β,则m⊥n是假命题;由于若m⊥α,n⊥β且α⊥β,不能确定两条直线的位置关系,故若m⊥α,n⊥β且α⊥β,则m∥n是假命题;由于m∥α,n⊥β且α⊥β不能确定两条直线的位置关系,故若m∥α,n⊥β且α⊥β,则m∥n是假命题;由于n∥β且α∥β可得出n?α或n∥α,又m⊥α可得出m⊥n故若m⊥α,n∥β且α∥β,则m⊥n是真命题.综上知,D选项正确,故选D
【分析】由题意,不同的两条直线m,n与两个平面α,β,A,D两个选项可由线线垂直的条件作作出判断,C,B两个选项可由线线平行的条件作出判断,得出正确选项本题的考点是间中直线一直线之间的位置关系,考查了线线平行与线线垂直的条件,解题的关键是理解题意,有着较强的空间立体感知能力,本题考查了空间想像能力,推理判断的能力,是高考中常见题型,其特点是涉及到的知识点多,知识容量大,因此备受高考命题者青睐
5.【答案】
C
【解析】①错,应写为A∈α
,
B∈α;②错,应写为AB?α;③错,推理错误,有可能A∈α;④推理与表述都正确.选C.
【分析】根据空间中点、线、面的位置关系可得结果。注意符号的正确使用。
6.【答案】D
【解析】解:∵α是一个平面,m,n是两条直线,A是一个点,
m?α,n?α,
∴n在平面a上,m与平面a相交
∵A∈m.A∈a
∴A是M和平面a相交的点
∴m和n
异面或相交,一定不平行.
故选:D.
【分析】由已知得n在平面a上,m与平面a相交,A是M和平面a相交的点,从而m和n
异面或相交,一定不平行.
7.【答案】
D
【解析】解:对于①,若A∈α,B∈α,C∈AB,根据平面的基本性质得到C∈α;故意正确;
对于②,若α∩β=l,b?α,c?β,b∩c=A,根据平面的基本性质容易得到A同时在两个平面内,即A∈l;故②正确;
对于③,A,B,C∈α,A,B,C∈β且A,B,C不共线,根据不共线的三点确定一个平面,容易得到α与β重合;故③正确;
对于④,任意三点不共线的四点不一定共面.比如空间四面体;故④错误;
故选D.
【分析】利用平面的基本性质对四个命题分别分析解答.
8.【答案】D
【解析】解:对于A,若a∥α,b∥a,说明b与平面α的平行线a平行,b可能在平面α内,它们的位置关系应该是平行或直线在平面内,故A错;
对于B,若a∥α,b∥α,a?β,b?β,说明在平面α和平面β内各有一条直线与另一个平面平行,但是条件并没有指明平面α、β的位置关系,平面α、β也可能相交,故不一定α∥β,故B错;
对于C,若α∥β,b∥α,说明直线b∥β或b?β,故不一定b∥β,故C错;
对于D,若α∥β,a?α,根据面面平行的性质:两个平行平面中的一个平面的直线必定平行于另一个平面,知a∥β,故D正确.
故选D.
【分析】对于A、B、C、D各项逐个加以分析:根据线面平行的判定及性质得到A错误;根据面面平行的判定得到B错误;根据面面平行的性质得到C错误;根据面面平行的性质,可得D正确.
9.【答案】
D
【解析】【分析】结合公理及正方体模型可以判断:A,B,C均有可能,可以利用反证法证明结论,也可以从具体的实物模型中去寻找反例证明.
【解答】如图,在正方体AC1中,
∵A1A⊥平面ABCD,∴A1A⊥AD,A1A⊥BC,
又∵AD∥BC,∴选项A有可能;
∵A1A⊥平面ABCD,∴A1A⊥AD,A1A⊥AB
,
又∵AD∩AB=A,∴选项B有可能;
∵A1A⊥平面ABCD,A1A⊥平面A1B1C1D1
,
∴A1A⊥AC,A1A⊥A1D1
,
又∵AC与A1D1不在同一平面内,∴选项C有可能.
故选D.
10.【答案】
C
【解析】设侧棱长是
,
底面的变长是
,点
到对角线
的距离
即为直角三角形
斜边
上的高,
,点
到平面
的距离分别
即为直角三角形
斜边
上的高,
若侧棱的长小于底面的变长,
即
,
A,B错误;
若侧棱的长大于底面的变长,
即
,
故答案为:C
【分析】设侧棱长是
b,
底面的变长是
a,点
B1到对角线
BD1的距离
h
即为直角三角形
△B1BD1
斜边
BD1上的高,得到点
B1到平面
A1BCD1的距离分别
d
即为直角三角形
△B1BA斜边B1A
上的高,得到,若侧棱的长小于底面的变长时,可判断A、B错误,若侧棱的长大于底面的变长,可判断C是正确的。
二、填空题
11.【答案】P∈l
【解析】因为m?α
,
n?β
,
m∩n=P
,
所以P∈α且P∈β.又α∈β=l
,
所以点P在直线l上,所以P∈l.【分析】根据平面的性质2,得到点P在平面和平面的交线上。
12.【答案】60°
【解析】连结BC1、A1C1
,
∵在正方体ABCD﹣A1B1C1D1中,A1A平行且等于C1C,
∴四边形AA1C1C为平行四边形,可得A1C1∥AC,
因此∠BA1C1(或其补角)是异面直线A1B与AC所成的角,设正方体的棱长为a,则△A1B1C中A1B=BC1=C1A1=a,
∴△A1B1C是等边三角形,可得∠BA1C1=60°,
即异面直线A1B与AC所成的角等于60°.
故答案为:60°.
【分析】连结BC1、A1C1
,
由正方体的性质可得四边形AA1C1C为平行四边形,从而A1C1∥AC,∠BA1C1是异面直线A1B与AC所成的角.然后求解异面直线A1B与AC所成的角.
13.【答案】①③
【解析】若直线与平面有两个公共点,则这条直线一定在这个平面内,故①正确;直线l在平面α内用符号“?”表示,即l?α,②错误;由a与b相交,说明两个平面有公共点,因此一定相交,故③正确.故答案为:①③
【分析】由平面的基本性质对各命题进行判断.
14.【答案】③④
【解析】解:对于①,不在同一直线上的三点确定一个平面,∴①错误;
对于②,不共点的三条两两相交的直线确定一个平面,∴②错误;
对于③,空间四点A、B、C、D不共面时,则四点构成一个三棱锥,如图:
当平面一侧有一点,另一侧有三点时,令截面与四棱锥的四个面之一平行,第四个顶点到这个截面的距离与其相对的面到此截面的距离相等,这样的平面有4个,
当平面一侧有两点,另一侧有两点时,即过相对棱的异面直线公垂线段的中点,且和两条相对棱平行的平面,满足条件.因三棱锥的相对棱有三对,则此时满足条件的平面个数是3个,
所以满足条件的平面恰有7个,③正确;
对于④,两个相交平面把空间分成四个区域是真命题,∴④正确.
综上,正确的命题序号是③④.
故答案为:③④.
【分析】①根据平面的公理“三点定面”即可判断命题错误;
②根据三条两两相交的直线可能不共面,即可判断命题错误;
③根据空间四点不共面时,四点构成一个三棱锥,讨论平面一侧有一点,另一侧有三点时,和平面一侧有两点,另一侧有两点时,满足条件的平面数是多少即可;
④根据实际情况即可得出结论正确.
三、解答题
15.【答案】
证明:如图所示,作
,
因为平面
平面
,
是平面
与平面
的交线,
,
所以
平面
,
,
因为
平面
,所以
,
因为
,所以
平面
,
。
【解析】【分析】本题首先可以作
,然后根据平面
平面
即可得出
,再然后通过
平面
即可得出
,最后通过线面垂直的相关证明以及性质即可得出结果。
16.【答案】
证明:取BD的中点O,连接AO,CO.
∵AB=AD,∴AO⊥BD,
∵CB=CD,∴CO⊥BD,
又AO∩CO=O,
∴BD⊥平面ACO,
AC?平面ACO,
∴BD⊥AC.
【解析】【分析】取BD的中点O,连接AO,CO.由等腰三角形的三线合一,得到AO⊥BD,CO⊥BD,再由线面垂直的判定定理得到BD⊥平面ACO,运用线面垂直的性质即可得证.
17.【答案】
(1)解:分别取AB,PA中点E,F,连接CE,EF,CF,NE,ME.
∵E是AB中点,点N是PB的中点,
∴
∵PA⊥面ABCD,
∴NE⊥面ABCD,NE⊥AB.
又∵MN∥BC,∴MN⊥AB.
所以:AB⊥MN,
得证.
(2)解:∵E是AB中点,F是PA中点E,N是PB的中点,点M是CD的中点
∴AM
CE,FE
.
所以:异面直线AM与PB所成角的大小即相交直线CF与EF所成角的大小
在△CEF中:EC=MA=
=
,FE=
,FC=
.
利用余弦定理:
cos∠FEC=
∵cos∠FEC<0,
∴∠FEC是钝角.
所以异面直线AM与PB所成角的大小为π﹣
【解析】【分析】(1)由题意,证明线线垂直,利用“三垂线定理或三垂线定理的逆定理”即可解决.(2)异面直线所成角,首先要构造出这两条异面直线的平行线相交的角,即为异面直线所成角.由题意,分别取AB,PA中点E,F,连接CE,EF,CF,所以异面直线AM与PB所成角的大小即相交直线CF与EF所成角的大小.
18.【答案】
解:(Ⅰ)以D为原点,DA,DC,DS为正交基底建立如图所示的空间直角坐标系D﹣xyz,
则各点的坐标为A(1,0,0),B(1,1,0),C(0,2,0),S(0,0,2).
=(0,2,﹣2),
=(1,1,﹣2),令
,
则
=(λ,λ,﹣2λ),
=
=(0,0,2)+(λ,λ,﹣2λ)=(λ,λ,2﹣2λ),
∵DE⊥SC,∴
=0,即2λ﹣2(2﹣2λ)=0,故
.
∴
=2
(Ⅱ)由(Ⅰ)知,
=(
),
=(﹣
),
设
=(x,y,z)为平面ADE的法向量,
则
,令y=1,得
=(0,1,﹣1)为平面ADE的法向量,
于是cos<
>=
=
=
,
∴直线EC与平面ADE所成角为
【解析】【分析】(Ⅰ)以D为原点,DA,DC,DS为正交基底建立如图所示的空间直角坐标系D﹣xyz,利用向量法能求出
的值.(Ⅱ)分别求出平面ADE的法向量和
,利用向量法能求出直线EC与平面ADE所成角.
19.【答案】证明:(I)∵△ABC是正三角形,M是AC中点,
∴BM⊥AC,即BD⊥AC.
又∵PA⊥平面ABCD,∴PA⊥BD.
又PA∩AC=A,∴BD⊥平面PAC.
∴BD⊥PC.
(Ⅱ)在正△ABC中,BM=2.
在△ACD中,
∵M为AC中点,DM⊥AC,∴AD=CD.
∠ADC=120°,
∴DM=,
∴=.
在等腰直角△PAB中,PA=AB=4,PB=4,
∴=,
∴,
∴MN∥PD.
又MN?平面PDC,PD?平面PDC,
∴MN∥平面PDC.
【解析】【分析】(Ⅰ)由正三角形的性质可得BD⊥AC,利用线面垂直的性质可知PA⊥BD,再利用线面垂直的判定定理即可证明BD⊥PC;
(Ⅱ)利用已知条件分别求出BM、MD、PB,得到
,
即可得到MN∥PD,再利用线面平行的判定定理即可证明
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
