高中物理第一章抛体运动3竖直方向的抛体运动课件粤教版必修2
文档属性
| 名称 | 高中物理第一章抛体运动3竖直方向的抛体运动课件粤教版必修2 |

|
|
| 格式 | zip | ||
| 文件大小 | 768.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-07-09 16:24:30 | ||
图片预览


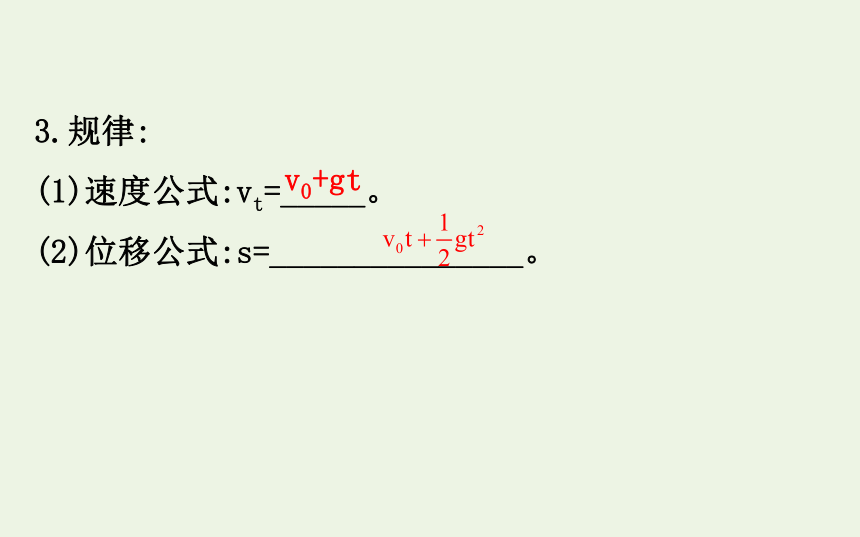









文档简介
(共53张PPT)
第三节
竖直方向的抛体运动
一、竖直下抛运动
1.定义:把物体以一定的初速度v0沿着竖直方向_____
抛出,仅在_____作用下物体所做的运动。
2.性质:初速度不为___,加速度a=__的匀加速直线运动。
向下
重力
零
g
3.规律:
(1)速度公式:vt=_____。
(2)位移公式:s=_______________。
v0+gt
【生活链接】
如图所示,张超小朋友在5楼的阳台上
由静止释放一块橡皮泥给楼下的小
朋友,试问:
橡皮泥做竖直下抛运动吗?经过3楼窗口的运动是不是竖直下抛运动?
提示:橡皮泥由静止释放,则橡皮泥做的不是竖直下抛运动;经过3楼窗口时,橡皮泥有了初速度,则是竖直下抛运动。
二、竖直上抛运动
1.定义:把物体以一定的初速度v0沿着竖直方向_____
抛出,仅在_____作用下物体所做的运动。
2.性质:初速度不为零,加速度a=
___的匀变速直线运
动。
向上
重力
-g
3.研究方法:
(2)整体法:竖直上抛运动是一种_______直线运动。
匀减速直线
自由落体
匀变速
4.规律:
(1)分段法:
v0-gt
gt′
③上升到最高点,所用时间t=_______。
④上升的最大高度:s=____________。
(2)整体法:
①在时刻t时的速度:vt=v0-gt。
②在时刻t的位移:s=v0t-
gt2。
【思考辨析】
(1)从正在上升的热气球上脱落的物体做自由落体运动。( )
(2)物体做竖直上抛运动时,上升过程中速度、加速度都在减小。
( )
(3)竖直上抛运动是匀减速直线运动。
( )
提示:(1)×。由于惯性,物体在气球上脱落时具有向上的初速度,若只受重力,将做竖直上抛运动。
(2)×。竖直上抛运动的上升阶段,物体的速度减小,加速度不变。
(3)×。竖直上抛运动上升阶段是匀减速直线运动,下降阶段是匀加速直线运动。
一 竖直下抛运动
考查角度1
竖直下抛运动的条件和规律
【典例1】关于竖直下抛运动,下列说法正确的是( )
A.飞行中的轰炸机抛下的炸弹的运动是竖直下抛运动
B.从屋顶竖直向下抛出的铅球的运动是竖直下抛运动
C.竖直下抛运动是一种特殊的非匀变速直线运动
D.某同学站在窗前将衣服竖直向下抛给伙伴,他认为衣服的运动是竖直下抛运动
【解析】选B。轰炸机抛下的炸弹具有水平初速度,不是竖直下抛运动,故A错;衣服向下运动时所受空气阻力太大,与其重力相比不可忽略,其运动不是竖直下抛运动,故D错;从屋顶竖直向下抛出的铅球具有竖直向下的初速度且其所受空气阻力可以忽略,其运动可以看作竖直下抛运动,故B正确;竖直下抛运动仅受重力作用,其加速度为重力加速度g,故C错。
【核心归纳】
1.做竖直下抛运动的条件:
(1)具有竖直向下的初速度。
(2)只受重力作用。
1.做竖直下抛运动的条件:
(1)具有竖直向下的初速度。
(2)只受重力作用。
2.规律:竖直下抛运动是初速度v0向下、加速度为g的
匀加速直线运动,其规律如下:(1)vt=v0+gt。
(2)s=v0t+
gt2。(3)
【易错提醒】
(1)竖直下抛运动不是自由落体运动,自由落体运动也不是竖直下抛运动。
(2)竖直向下抛出的物体,若空气阻力远小于重力,就可以把物体的运动看作是竖直下抛运动。
考查角度2
竖直下抛运动问题的分析方法
【典例2】跳伞运动员以5
m/s的速度竖直匀速降落,在离地面h=10
m的地方掉了一颗扣子,跳伞运动员比扣子晚着陆的时间为(扣子受到的空气阻力可忽略,g取10
m/s2)
( )
A.2
s
B.
s
C.1
s
D.(2-
)
s
【解析】选C。跳伞运动员掉下扣子后的着陆时间
t1=
=2
s,扣子的着地时间设为t2,则有
h=vt2+
即10
m=5t2+
,解得t2=1
s。故
Δt=1
s,C正确。
【核心归纳】
1.竖直下抛运动问题的处理方法:
(1)竖直下抛运动是一种特殊的匀变速直线运动,所有匀变速运动的公式和推论均适用于竖直下抛运动。
(2)从运动的合成与分解的角度看,竖直下抛运动是匀速直线运动和自由落体运动两个分运动的合运动。
2.竖直下抛运动v-t图象:
合运动图象见图甲,分运动图象见乙、丙:
【过关训练】
1.将物体以一定的初速度竖直下抛,其速度-时间图象可能是
( )
【解析】选C。竖直下抛运动的速度与时间的关系式为vt=v0+gt,可知C正确。
2.一个热气球停在空中某一高度处,某时刻甲物体从热气球下的吊篮中自由落下,经t0=3
s后,吊篮中的人以初速度v0=40
m/s竖直向下抛出乙物体,试求(g取
10
m/s2):
(1)乙物体经过多长时间与甲物体相遇?
(2)如果乙物体抛出后5
s落到地面上,则吊篮离地面多高?
【解析】(1)设乙物体抛出后经时间t与甲物体相遇,这
时甲物体与吊篮的距离为:s1=
g(t+t0)2
乙物体与吊篮的距离为:s2=v0t+
gt2
甲与乙相遇,则s1=s2
代入相关数据解得:t=4.5
s
(2)吊篮离地面高度为:
H=v0t′+
gt′2
=40×5
m+
×10×52
m
=325
m
答案:(1)4.5
s (2)325
m
【补偿训练】
从离地45
m处自由下落一个小球,1
s后再从同一位置竖直向下抛出另一个小球,要使两个小球同时落地,第二个小球抛出时的初速度必须多大?(不计空气阻力,g取10
m/s2)
【解析】设自由下落的小球运动时间为t,则
设下抛小球的初速度为v0,则运动时间为t1=2
s,
由位移公式
得
答案:12.5
m/s
二 竖直上抛运动
【典例气球上系一重物,以10
m/s的速度自地面匀速上升①。当上升到离地面高度h=40
m处时,绳子突然断了②。问:
(1)重物是否立即下降。重物要经过多长时间才能落到地面。
(2)重物落地时的速度多大?(g取10
m/s2)
【审题关键】
序号
信息提取
①
绳子断时,重物竖直上抛的初速度为
10
m/s
②
重物从离地面40
m的高处做竖直上抛运动
【解析】(1)绳子突然断时,重物与气球具有相同的速
度,由于惯性,重物将继续向上运动,上升一段距离到
达最高点后再做自由落体运动。上升过程:上升时间
t=
=1
s,自40
m高处继续上升的最大高
度:hm=
=5
m,重物做自由落体运动的过程:下降的
总高度H=hm+h=45
m,由h=
gt2可求得下降的时间
t下=3
s。
重物从绳子断到落地的总时间:t总=t+t下=4
s。
(2)重物落地时的速度vt=gt下=30
m/s。
答案:(1)否 4
s (2)30
m/s
【核心归纳】
1.运动性质:初速度不为零的匀变速直线运动。
2.特征:
(1)具有竖直向上的初速度。
(2)物体只受重力作用,加速度恒为重力加速度。
3.分解:竖直上抛运动可看作初速度为v0、方向竖直向上的匀速直线运动和自由落体运动的合运动。
4.竖直上抛运动的对称性:
(1)速度对称:上升阶段和下落阶段经过同一位置时速度等大反向,即v上=-v下。
(2)时间对称:上升阶段与下落阶段经过同一段竖直距离所用的时间相等,即t上=t下。
5.竖直上抛运动问题的分析方法:
(1)分段法。
①上升过程:匀减速直线运动,取向上为正方向。
②下降过程:自由落体运动。
(2)整体法。
匀减速直线运动,取向上为正方向,则v0>0,a=-g,
【特别提醒】
(1)注意方程的矢量性,选取正方向后,凡是与正方向相同的矢量取正值,相反的取负值。
(2)注意竖直上抛运动的对称性可能出现多解问题。
【过关训练】
1.气球以速度v匀速上升,途中从气球上掉下一物体,物体相对于地面运动的v-t图象是图中的
( )
【解析】选D。从气球上掉下来的物体由于惯性保持原有的运动,即具有一竖直向上的初速度v,物体由于具有初速度v,所以在离开气球后要继续上升,一直到速度为0,这一过程可以视为加速度为-g的匀减速直线运动,之后速度反向并增大。
2.竖直上抛的物体,初速度是30
m/s,经过2
s产生的位移是多少?路程是多少?经过4
s产生的位移是多少?路程是多少?(空气阻力不计,g取10
m/s2)
【解析】物体上升的时间为:t0=
=3
s。
物体以30
m/s的初速度做竖直上抛运动,根据位移—时
间关系公式,有:
x=v0t-
gt2=30×2
m-
×10×4
m=40
m。
没有到达最高点,所以路程等于位移的大小,
即:x=s=40
m。
上升的高度为:h=
g
=
×10×9
m=45
m。
下降的位移为:h′=
gt′2=
×10×1
m=5
m。
故位移为:x′=h-h′=45
m-5
m=40
m。
路程为:s′=h+h′=45
m+5
m=50
m。
答案:40
m 40
m 40
m 50
m
【拓展例题】
考查内容:竖直方向抛体运动的综合应用
【典例】子弹从枪口射出速度大小是30
m/s,某人每隔1
s竖直向上开一枪,假定子弹在升降过程中都不相碰,试求:
(1)空中最多能有几颗子弹?
(2)设在t=0时将第1颗子弹射出,在什么时刻它和第2颗子弹在空中相遇而过?
(3)这些子弹在距原处多高的地方依次与第1颗子弹相遇?(不计空气阻力)
【解析】(1)子弹在空中经过的时间t=
=6
s。t=0时第1颗子弹射出,它于第6
s末回到原处;同
时第7颗子弹即将射出,在第6颗子弹射出后,第1颗子弹
尚未返回原处时,空中共有6颗子弹,第7颗子弹射出时,
第1颗子弹已落地,所以空中最多有6颗子弹。
(2)设第1颗子弹在空中运动t
s
,
依题意第2颗子弹运动(t-1)
s,两子弹在空中相遇,则
v1=v0-gt,v2=v0-g(t-1)。
由于子弹初速度相同,按对称性有v1=-v2,
即v0-gt=-[v0-g(t-1)],解得t=3.5
s。
说明第1颗子弹发射3.5
s末,第2颗子弹发射2.5
s末,两颗子弹在空中相遇。
(3)距原处高度
式中t用第1颗子
弹从最高点下落0.5
s、1.0
s、1.5
s、2.0
s、
2.5
s代入即得:h12=43.75
m;h13=40
m;h14=33.75
m;
h15=25
m;h16=13.75
m。
答案:(1)6颗 (2)3.5
s
(3)43.75
m、40
m、33.75
m、25
m、13.75
m
第三节
竖直方向的抛体运动
一、竖直下抛运动
1.定义:把物体以一定的初速度v0沿着竖直方向_____
抛出,仅在_____作用下物体所做的运动。
2.性质:初速度不为___,加速度a=__的匀加速直线运动。
向下
重力
零
g
3.规律:
(1)速度公式:vt=_____。
(2)位移公式:s=_______________。
v0+gt
【生活链接】
如图所示,张超小朋友在5楼的阳台上
由静止释放一块橡皮泥给楼下的小
朋友,试问:
橡皮泥做竖直下抛运动吗?经过3楼窗口的运动是不是竖直下抛运动?
提示:橡皮泥由静止释放,则橡皮泥做的不是竖直下抛运动;经过3楼窗口时,橡皮泥有了初速度,则是竖直下抛运动。
二、竖直上抛运动
1.定义:把物体以一定的初速度v0沿着竖直方向_____
抛出,仅在_____作用下物体所做的运动。
2.性质:初速度不为零,加速度a=
___的匀变速直线运
动。
向上
重力
-g
3.研究方法:
(2)整体法:竖直上抛运动是一种_______直线运动。
匀减速直线
自由落体
匀变速
4.规律:
(1)分段法:
v0-gt
gt′
③上升到最高点,所用时间t=_______。
④上升的最大高度:s=____________。
(2)整体法:
①在时刻t时的速度:vt=v0-gt。
②在时刻t的位移:s=v0t-
gt2。
【思考辨析】
(1)从正在上升的热气球上脱落的物体做自由落体运动。( )
(2)物体做竖直上抛运动时,上升过程中速度、加速度都在减小。
( )
(3)竖直上抛运动是匀减速直线运动。
( )
提示:(1)×。由于惯性,物体在气球上脱落时具有向上的初速度,若只受重力,将做竖直上抛运动。
(2)×。竖直上抛运动的上升阶段,物体的速度减小,加速度不变。
(3)×。竖直上抛运动上升阶段是匀减速直线运动,下降阶段是匀加速直线运动。
一 竖直下抛运动
考查角度1
竖直下抛运动的条件和规律
【典例1】关于竖直下抛运动,下列说法正确的是( )
A.飞行中的轰炸机抛下的炸弹的运动是竖直下抛运动
B.从屋顶竖直向下抛出的铅球的运动是竖直下抛运动
C.竖直下抛运动是一种特殊的非匀变速直线运动
D.某同学站在窗前将衣服竖直向下抛给伙伴,他认为衣服的运动是竖直下抛运动
【解析】选B。轰炸机抛下的炸弹具有水平初速度,不是竖直下抛运动,故A错;衣服向下运动时所受空气阻力太大,与其重力相比不可忽略,其运动不是竖直下抛运动,故D错;从屋顶竖直向下抛出的铅球具有竖直向下的初速度且其所受空气阻力可以忽略,其运动可以看作竖直下抛运动,故B正确;竖直下抛运动仅受重力作用,其加速度为重力加速度g,故C错。
【核心归纳】
1.做竖直下抛运动的条件:
(1)具有竖直向下的初速度。
(2)只受重力作用。
1.做竖直下抛运动的条件:
(1)具有竖直向下的初速度。
(2)只受重力作用。
2.规律:竖直下抛运动是初速度v0向下、加速度为g的
匀加速直线运动,其规律如下:(1)vt=v0+gt。
(2)s=v0t+
gt2。(3)
【易错提醒】
(1)竖直下抛运动不是自由落体运动,自由落体运动也不是竖直下抛运动。
(2)竖直向下抛出的物体,若空气阻力远小于重力,就可以把物体的运动看作是竖直下抛运动。
考查角度2
竖直下抛运动问题的分析方法
【典例2】跳伞运动员以5
m/s的速度竖直匀速降落,在离地面h=10
m的地方掉了一颗扣子,跳伞运动员比扣子晚着陆的时间为(扣子受到的空气阻力可忽略,g取10
m/s2)
( )
A.2
s
B.
s
C.1
s
D.(2-
)
s
【解析】选C。跳伞运动员掉下扣子后的着陆时间
t1=
=2
s,扣子的着地时间设为t2,则有
h=vt2+
即10
m=5t2+
,解得t2=1
s。故
Δt=1
s,C正确。
【核心归纳】
1.竖直下抛运动问题的处理方法:
(1)竖直下抛运动是一种特殊的匀变速直线运动,所有匀变速运动的公式和推论均适用于竖直下抛运动。
(2)从运动的合成与分解的角度看,竖直下抛运动是匀速直线运动和自由落体运动两个分运动的合运动。
2.竖直下抛运动v-t图象:
合运动图象见图甲,分运动图象见乙、丙:
【过关训练】
1.将物体以一定的初速度竖直下抛,其速度-时间图象可能是
( )
【解析】选C。竖直下抛运动的速度与时间的关系式为vt=v0+gt,可知C正确。
2.一个热气球停在空中某一高度处,某时刻甲物体从热气球下的吊篮中自由落下,经t0=3
s后,吊篮中的人以初速度v0=40
m/s竖直向下抛出乙物体,试求(g取
10
m/s2):
(1)乙物体经过多长时间与甲物体相遇?
(2)如果乙物体抛出后5
s落到地面上,则吊篮离地面多高?
【解析】(1)设乙物体抛出后经时间t与甲物体相遇,这
时甲物体与吊篮的距离为:s1=
g(t+t0)2
乙物体与吊篮的距离为:s2=v0t+
gt2
甲与乙相遇,则s1=s2
代入相关数据解得:t=4.5
s
(2)吊篮离地面高度为:
H=v0t′+
gt′2
=40×5
m+
×10×52
m
=325
m
答案:(1)4.5
s (2)325
m
【补偿训练】
从离地45
m处自由下落一个小球,1
s后再从同一位置竖直向下抛出另一个小球,要使两个小球同时落地,第二个小球抛出时的初速度必须多大?(不计空气阻力,g取10
m/s2)
【解析】设自由下落的小球运动时间为t,则
设下抛小球的初速度为v0,则运动时间为t1=2
s,
由位移公式
得
答案:12.5
m/s
二 竖直上抛运动
【典例气球上系一重物,以10
m/s的速度自地面匀速上升①。当上升到离地面高度h=40
m处时,绳子突然断了②。问:
(1)重物是否立即下降。重物要经过多长时间才能落到地面。
(2)重物落地时的速度多大?(g取10
m/s2)
【审题关键】
序号
信息提取
①
绳子断时,重物竖直上抛的初速度为
10
m/s
②
重物从离地面40
m的高处做竖直上抛运动
【解析】(1)绳子突然断时,重物与气球具有相同的速
度,由于惯性,重物将继续向上运动,上升一段距离到
达最高点后再做自由落体运动。上升过程:上升时间
t=
=1
s,自40
m高处继续上升的最大高
度:hm=
=5
m,重物做自由落体运动的过程:下降的
总高度H=hm+h=45
m,由h=
gt2可求得下降的时间
t下=3
s。
重物从绳子断到落地的总时间:t总=t+t下=4
s。
(2)重物落地时的速度vt=gt下=30
m/s。
答案:(1)否 4
s (2)30
m/s
【核心归纳】
1.运动性质:初速度不为零的匀变速直线运动。
2.特征:
(1)具有竖直向上的初速度。
(2)物体只受重力作用,加速度恒为重力加速度。
3.分解:竖直上抛运动可看作初速度为v0、方向竖直向上的匀速直线运动和自由落体运动的合运动。
4.竖直上抛运动的对称性:
(1)速度对称:上升阶段和下落阶段经过同一位置时速度等大反向,即v上=-v下。
(2)时间对称:上升阶段与下落阶段经过同一段竖直距离所用的时间相等,即t上=t下。
5.竖直上抛运动问题的分析方法:
(1)分段法。
①上升过程:匀减速直线运动,取向上为正方向。
②下降过程:自由落体运动。
(2)整体法。
匀减速直线运动,取向上为正方向,则v0>0,a=-g,
【特别提醒】
(1)注意方程的矢量性,选取正方向后,凡是与正方向相同的矢量取正值,相反的取负值。
(2)注意竖直上抛运动的对称性可能出现多解问题。
【过关训练】
1.气球以速度v匀速上升,途中从气球上掉下一物体,物体相对于地面运动的v-t图象是图中的
( )
【解析】选D。从气球上掉下来的物体由于惯性保持原有的运动,即具有一竖直向上的初速度v,物体由于具有初速度v,所以在离开气球后要继续上升,一直到速度为0,这一过程可以视为加速度为-g的匀减速直线运动,之后速度反向并增大。
2.竖直上抛的物体,初速度是30
m/s,经过2
s产生的位移是多少?路程是多少?经过4
s产生的位移是多少?路程是多少?(空气阻力不计,g取10
m/s2)
【解析】物体上升的时间为:t0=
=3
s。
物体以30
m/s的初速度做竖直上抛运动,根据位移—时
间关系公式,有:
x=v0t-
gt2=30×2
m-
×10×4
m=40
m。
没有到达最高点,所以路程等于位移的大小,
即:x=s=40
m。
上升的高度为:h=
g
=
×10×9
m=45
m。
下降的位移为:h′=
gt′2=
×10×1
m=5
m。
故位移为:x′=h-h′=45
m-5
m=40
m。
路程为:s′=h+h′=45
m+5
m=50
m。
答案:40
m 40
m 40
m 50
m
【拓展例题】
考查内容:竖直方向抛体运动的综合应用
【典例】子弹从枪口射出速度大小是30
m/s,某人每隔1
s竖直向上开一枪,假定子弹在升降过程中都不相碰,试求:
(1)空中最多能有几颗子弹?
(2)设在t=0时将第1颗子弹射出,在什么时刻它和第2颗子弹在空中相遇而过?
(3)这些子弹在距原处多高的地方依次与第1颗子弹相遇?(不计空气阻力)
【解析】(1)子弹在空中经过的时间t=
=6
s。t=0时第1颗子弹射出,它于第6
s末回到原处;同
时第7颗子弹即将射出,在第6颗子弹射出后,第1颗子弹
尚未返回原处时,空中共有6颗子弹,第7颗子弹射出时,
第1颗子弹已落地,所以空中最多有6颗子弹。
(2)设第1颗子弹在空中运动t
s
,
依题意第2颗子弹运动(t-1)
s,两子弹在空中相遇,则
v1=v0-gt,v2=v0-g(t-1)。
由于子弹初速度相同,按对称性有v1=-v2,
即v0-gt=-[v0-g(t-1)],解得t=3.5
s。
说明第1颗子弹发射3.5
s末,第2颗子弹发射2.5
s末,两颗子弹在空中相遇。
(3)距原处高度
式中t用第1颗子
弹从最高点下落0.5
s、1.0
s、1.5
s、2.0
s、
2.5
s代入即得:h12=43.75
m;h13=40
m;h14=33.75
m;
h15=25
m;h16=13.75
m。
答案:(1)6颗 (2)3.5
s
(3)43.75
m、40
m、33.75
m、25
m、13.75
m
同课章节目录
- 第一章 抛体运动
- 第01节 什么是抛体运动
- 第02节 运动的合成与分解
- 第03节 竖直方向的抛体运动
- 第04节 平抛运动
- 第05节 斜抛运动
- 第二章 圆周运动
- 第01节 匀速圆周运动
- 第02节 向心力
- 第03节 离心现象及其应用
- 第三章 万有引力定律及其应用
- 第01节 万有引力定律
- 第02节 万有引力定律的应用
- 第03节 飞向太空
- 第四章 机械能和能源
- 第01节 功
- 第02节 动能 势能
- 第03节 探究外力做功与物体动能变化的关系
- 第04节 机械能守恒定律
- 第05节 验证机械能守恒定律
- 第06节 能量 能量转化与守恒定律
- 第07节 功率
- 第08节 能源的开发与利用
- 第五章 经典力学与物理学的革命
- 第01节 经典力学的成就与局限性
- 第02节 经典时空观与相对论时空观
- 第03节 量子化现象
- 第04节 物理学——人类文明进步的阶梯
