正方形学案
图片预览
文档简介
§19.2.3 正方形
课型:综合解决课 设计时间:2018-09-24
学习目标:
掌握正方形的概念,知道正方形一切性质和判定,并会用它们进行有关的论证和计算。
学习重点:正方形的定义及正方形与平行四边形、矩形、菱形的联系.
学习难点:正方形与矩形、菱形的关系及正方形性质与判定的灵活运用.
学法指导:在小组讨论中通过互相学习,让学生体验合作学习的乐趣。
导学过程:
一、自主学习
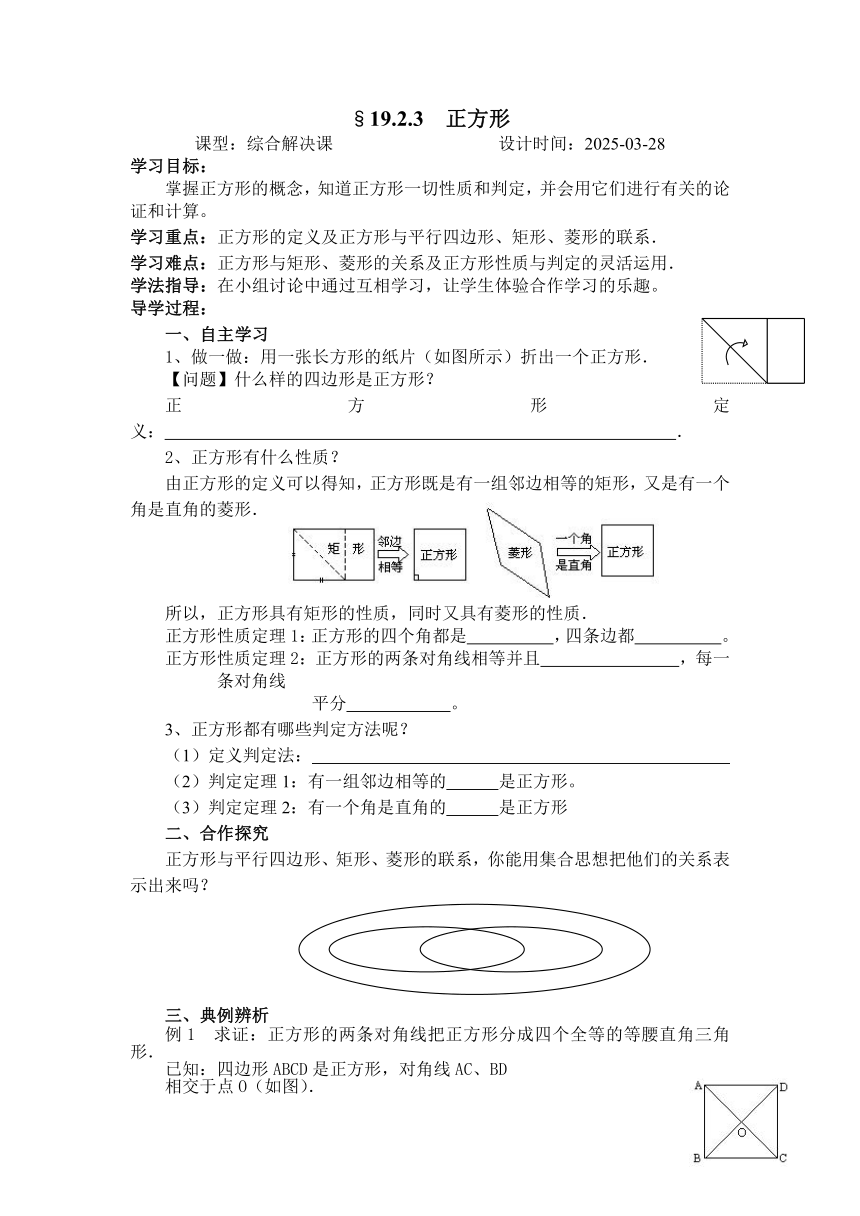
1、做一做:用一张长方形的纸片(如图所示)折出一个正方形.
【问题】什么样的四边形是正方形?
正方形定义: .
2、正方形有什么性质?
由正方形的定义可以得知,正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形.
所以,正方形具有矩形的性质,同时又具有菱形的性质.
正方形性质定理1:正方形的四个角都是 ,四条边都 。
正方形性质定理2:正方形的两条对角线相等并且 ,每一条对角线
平分 。
3、正方形都有哪些判定方法呢?
(1)定义判定法:
(2)判定定理1:有一组邻边相等的 是正方形。
(3)判定定理2:有一个角是直角的 是正方形
二、合作探究
正方形与平行四边形、矩形、菱形的联系,你能用集合思想把他们的关系表示出来吗?
三、典例辨析
例1 求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形.
已知:四边形ABCD是正方形,对角线AC、BD
相交于点O(如图).
求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
证明:
例2 .已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.
求证:(1)EA=AF; (2)EA⊥AF.
四、巩固练习
1.⑴正方形的四条边____ __,四个角___ ____,两条对角线____ _______ _.
⑵正方形的两条对角线把正方形分成四个全等的__________________
⑶正方形的边长为6,则面积为__________
⑷正方形的对角线长为6,则面积为__________
2.如右图,E为正方形ABCD边AB上的一点,已知EC=30, EB=10,
则正方形ABCD的面积为_______________,对角线为______ ____.
3.如右图,E为正方形ABCD内一点,且△EBC是等边三角形,
求∠EAD与∠ECD的度数.
五、课堂小结
课外作业
1.正方形ABCD的对角线相交于O,若AB=2,那么△ABO的
周长是______,△ABO面积是________.
2.如图,已知E点在正方形ABCD的BC边的延长线上,
且CE=AC,AE与CD相交于点F,则∠AFC=________.
3.顺次连接正方形各边中点的小正方形的面积是原正方形面积的( ).
A. B. C. D.
4.四条边都相等的四边形一定是( )
A.正方形 B.菱形 C.矩形 D.以上结论都不对
5.如图所示的运动:正方形ABCD和正方形AKCM中,将正方形AKLM沿点A向左旋转某个角度.连线段MD、KB,它们能相等吗?请证明你的结论.
课型:综合解决课 设计时间:2018-09-24
学习目标:
掌握正方形的概念,知道正方形一切性质和判定,并会用它们进行有关的论证和计算。
学习重点:正方形的定义及正方形与平行四边形、矩形、菱形的联系.
学习难点:正方形与矩形、菱形的关系及正方形性质与判定的灵活运用.
学法指导:在小组讨论中通过互相学习,让学生体验合作学习的乐趣。
导学过程:
一、自主学习
1、做一做:用一张长方形的纸片(如图所示)折出一个正方形.
【问题】什么样的四边形是正方形?
正方形定义: .
2、正方形有什么性质?
由正方形的定义可以得知,正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形.
所以,正方形具有矩形的性质,同时又具有菱形的性质.
正方形性质定理1:正方形的四个角都是 ,四条边都 。
正方形性质定理2:正方形的两条对角线相等并且 ,每一条对角线
平分 。
3、正方形都有哪些判定方法呢?
(1)定义判定法:
(2)判定定理1:有一组邻边相等的 是正方形。
(3)判定定理2:有一个角是直角的 是正方形
二、合作探究
正方形与平行四边形、矩形、菱形的联系,你能用集合思想把他们的关系表示出来吗?
三、典例辨析
例1 求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形.
已知:四边形ABCD是正方形,对角线AC、BD
相交于点O(如图).
求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
证明:
例2 .已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.
求证:(1)EA=AF; (2)EA⊥AF.
四、巩固练习
1.⑴正方形的四条边____ __,四个角___ ____,两条对角线____ _______ _.
⑵正方形的两条对角线把正方形分成四个全等的__________________
⑶正方形的边长为6,则面积为__________
⑷正方形的对角线长为6,则面积为__________
2.如右图,E为正方形ABCD边AB上的一点,已知EC=30, EB=10,
则正方形ABCD的面积为_______________,对角线为______ ____.
3.如右图,E为正方形ABCD内一点,且△EBC是等边三角形,
求∠EAD与∠ECD的度数.
五、课堂小结
课外作业
1.正方形ABCD的对角线相交于O,若AB=2,那么△ABO的
周长是______,△ABO面积是________.
2.如图,已知E点在正方形ABCD的BC边的延长线上,
且CE=AC,AE与CD相交于点F,则∠AFC=________.
3.顺次连接正方形各边中点的小正方形的面积是原正方形面积的( ).
A. B. C. D.
4.四条边都相等的四边形一定是( )
A.正方形 B.菱形 C.矩形 D.以上结论都不对
5.如图所示的运动:正方形ABCD和正方形AKCM中,将正方形AKLM沿点A向左旋转某个角度.连线段MD、KB,它们能相等吗?请证明你的结论.
