高中物理第四章机械能和能源2动能势能课件粤教版必修2 81张PPT
文档属性
| 名称 | 高中物理第四章机械能和能源2动能势能课件粤教版必修2 81张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 992.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-07-10 09:24:50 | ||
图片预览











文档简介
(共81张PPT)
第二节
动能 势能
一、功和能的关系
1.能量:一个物体能够对其他物体_____,则该物体具有能量。
做功
2.功与能的关系:
(1)做功的过程就是_________的过程,做了多少功,就
有多少能量发生转化,所以功是_________的量度。
(2)功和能的单位相同,在国际单位制中,都是______。
能量转化
能量转化
焦(J)
【生活链接】
某物理过程中发生了能量转化,那么能量转化了多少可通过何种思路来求解呢?
提示:功是能量转化的量度,可先求解做功多少,再确定能量转化多少,两者数值相等。
二、动能
1.定义:物体由于_____而具有的_____叫作_____。
2.推导:动能与其质量和速度大小的定量关系。
运动
能量
动能
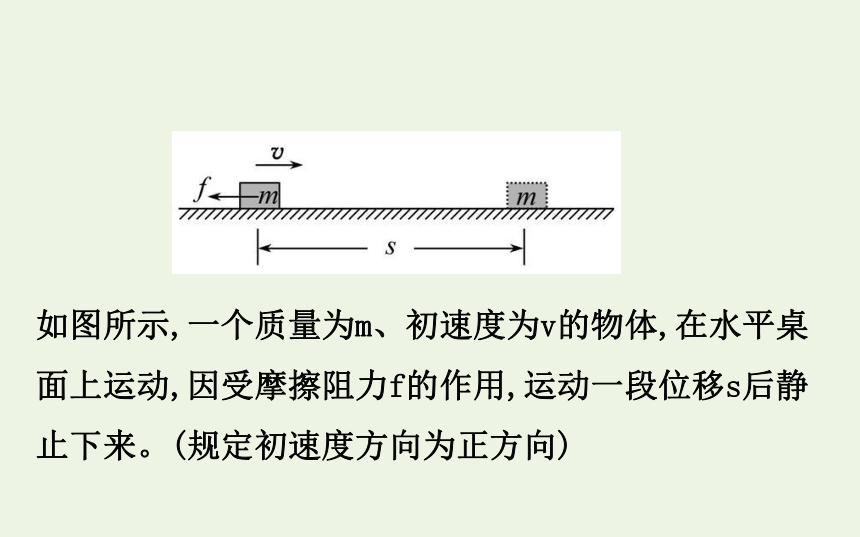
如图所示,一个质量为m、初速度为v的物体,在水平桌面上运动,因受摩擦阻力f的作用,运动一段位移s后静止下来。(规定初速度方向为正方向)
m(-a)
2(-a)s
3.表达式:Ek=______。
(1)物理意义:物体的动能等于___________与它的
_______________的一半。
(2)动能是__(A.标量 B.矢量),是__(A.过程 B.状
态)量。
4.单位:动能的国际单位是_____,简称焦,用符号J表示。
物体的质量
速度的平方乘积
A
B
焦耳
【思考辨析】
(1)两个物体中,速度大的动能也大。
( )
(2)某物体的速度加倍,它的动能也加倍。
( )
(3)做匀速圆周运动的物体的动能保持不变。
( )
提示:(1)×。动能的表达式为Ek=
mv2,即物体的动能大小由质量和速度大小共同决定,速度大的物体的动能不一定大。
(2)×。由Ek=
mv2知,某物体的速度加倍,它的动能变为原来的4倍。
(3)√。由于匀速圆周运动的线速度大小不变,故由
Ek=
mv2知做匀速圆周运动的物体的动能保持不变。
三、重力势能
1.概念:由物体所处位置的_____决定的能量。
高度
2.重力做的功:
(1)做功表达式:WG=mgh=mgh1-mgh2,式中h指初位置与末
位置的_______;h1、h2分别指_______、_______的高
度。
(2)做功的正负:物体_____时重力做正功;物体被_____
时重力做负功。
高度差
初位置
末位置
下降
举高
(3)做功的特点:物体运动时,重力对它做的功只跟它的
_________________有关,而跟物体运动的_____无关。
起点和终点的位置
路径
3.重力势能:
(1)定义:物体的重力与所处高度的乘积。
(2)大小:表达式:Ep=____;单位:_____,符号:J。
(3)标矢性:重力势能是_____,只有大小,没有方向。
mgh
焦耳
标量
(4)重力做功与重力势能变化的关系。
①表达式:WG=______。
②两种情况:
Ep1-Ep2
减少
增加
4.重力势能的相对性:
(1)参考平面:物体的重力势能总是相对于某一_______
来说的,这个_______叫作参考平面。在参考平面上,物
体的重力势能取作__。
水平面
水平面
0
(2)重力势能的相对性特点。
①选择不同的参考平面,物体重力势能的数值是_____
的。
②对选定的参考平面,上方物体的重力势能是___值,下
方物体的重力势能是___值,负号表示物体在这个位置具
有的重力势能要比在参考平面上具有的重力势能___。
不同
正
负
小
5.重力势能的系统性:重力势能是由_____和地面上物
体的_________决定的。
地球
相对位置
【思考辨析】
(1)物体的高度只要发生变化,其重力一定做功。
( )
(2)重力做功多少取决于物体的重力和它通过的路程。
( )
(3)重力势能Ep1=2
J,Ep2=-3
J,则Ep1与Ep2方向相反。
( )
(4)同一物体的重力势能Ep1=2
J,Ep2=-3
J,则Ep1>Ep2。
( )
提示:(1)√。无论做什么运动,只要物体的高度发生变化,其重力一定做功。
(2)×。重力做功多少取决于物体的重力大小和它在初、末位置的高度差。
(3)×。重力势能是标量,没有方向。
(4)√。重力势能为正值,表示物体处于参考平面的上方,为负值表示物体处于参考平面的下方,而同一物体在越高的地方重力势能越大。
四、弹性势能
1.定义:物体由于_________而具有的能量。
2.大小:跟_____的大小有关,_______越大,弹性势能也
越大。对于弹簧来说,弹性势能与_______________有
关。
3.势能:与相互作用物体的_________有关的能量。
发生形变
形变
形变量
拉伸或压缩长度
相对位置
【生活链接】
运动员将箭射出瞬间,弓要恢复原状,此过程中弓的弹性势能怎么变化?
提示:弓的形变量逐渐减小,弹性势能减小。
一 动能、重力势能的理解
考查角度1
动能的理解
【典例1】质量为2
kg的物体A以
5
m/s的速度向北运动,另一个质量为0.5
kg的物体B以
10
m/s的速度向西运动,则下列说法正确的是
( )
A.EkA=EkB
B.EkA>EkB
C.EkAD.因运动方向不同,无法比较动能
【解题探究】(1)动能为______(A.标量,B.矢量)。?
(2)动能的大小与速度的方向______(A.有,B.无)关。?
A
B
【解析】选A。根据Ek=
mv2知,EkA=25
J,EkB=25
J,而且动能是标量,所以EkA=EkB,A项正确。
【核心归纳】
(1)动能为状态量,只有正值,与速度的方向无关。
(2)由于速度具有相对性,所以动能也具有相对性。
(3)高中阶段通常取地面为参考系,讨论物体的速度和动能。
考查角度2
重力势能的理解
【典例2】一根粗细均匀的长直铁棒重①600
N,平放在水平地面上。现将一端从地面抬高0.50
m,
而另一端仍在地面上②,则
( )
A.铁棒的重力势能增加了300
J
B.铁棒的重力势能增加了150
J
C.铁棒的重力势能增加量为0
D.铁棒重力势能增加多少与参考平面选取有关,所以无法确定
【审题关键】
序号
信息提取
①
重心在棒的中点上
②
重心升高0.25
m
【解析】选B。铁棒的重心升高的高度h=0.25
m,铁棒增加的重力势能等于克服重力做的功,与参考平面选取无关,即ΔEp=mgh=600×0.25
J=150
J,故B正确。
【核心归纳】
1.重力势能的三性:
(1)标量性:重力势能是标量,只有大小,没有方向,但有正负。重力势能正负的含义:正、负值分别表示物体处于参考平面上方和下方。
(2)相对性:表达式Ep=mgh中的h是相对于参考平面的高度,故重力势能也具有相对性。计算重力势能时必须要选取参考平面,处于参考平面上的任何物体的重力势能都为零。
(3)系统性:重力是地球对物体的吸引而产生的,如果没有地球对物体的吸引,就不会有重力,也不存在重力势能,所以重力势能是这个系统共同具有的。平时所说的“物体的重力势能”只是一种简化的说法。
2.重力势能变化的绝对性:物体在两个高度不同的位置时,由于高度差一定,重力势能之差也是一定的,即物体的重力势能的变化与参考平面的选取无关。
【特别提醒】
(1)零势能面的选择是任意的,在实际应用中,应以解决问题方便为原则选择零势能面。
(2)如果在同一个问题中涉及多个物体的重力势能时,必须选取一个统一的参考平面。
(3)重力势能的正负表示重力势能的大小,正的总比负的大,如2
J>-5
J。
【过关训练】
1.(多选)改变汽车的质量和速度,都能使汽车的动能发生变化,则下列说法中正确的是
( )
A.质量不变,速度增大到原来的2倍,动能增大为原来的2倍
B.速度不变,质量增大到原来的2倍,动能增大为原来的2倍
C.质量减半,速度增大到原来的4倍,动能增大为原来的2倍
D.速度减半,质量增大到原来的4倍,动能不变
【解析】选B、D。动能Ek=
mv2,所以质量m不变,速度
v增大为原来的2倍时,动能Ek增大为原来的4倍,A错误;
速度不变,质量m增大为原来的2倍,则动能Ek也增大为
原来的2倍,B正确;若质量减半,速度增大为原来的4倍,
则动能增大为原来的8倍,C错误;速度v减半,质量增大
为原来的4倍,则Ek′=
×4m
=
mv2=Ek,即动能不
变,D正确。
2.如图所示,桌面距地面0.8
m,一物体质量为2
kg,放在距桌面0.4
m的支架上(g取10
m/s2)。以地面为参考平面,计算物体具有的重力势能,并计算物体由支架下落到桌面的过程中,重力势能减少了多少?
【解析】以地面为参考平面,物体的高度为:
h1=1.2
m。
物体的重力势能为:
Ep1=mgh1=2×10×1.2
J=24
J
物体落至桌面时的高度h2=0.8
m,重力势能为:
Ep2=mgh2=2×10×0.8
J=16
J
物体重力势能的减少量为:
ΔEp=Ep1-Ep2=(24-16)
J=8
J。
答案:24
J 8
J
【补偿训练】
1.关于重力势能的说法正确的是
( )
A.重力势能由重物本身因素决定
B.因为重力势能有负值,所以说重力势能是矢量
C.重力做功才有重力势能,重力不做功,物体就不具有重力势能
D.重力做功引起重力势能变化
【解析】选D。重力势能与重物的重量、高度等有关,A错误。重力势能是标量,其负值表示重物高度低于零势能面,B错误。重力做功时重力势能发生改变,但不做功时物体也具有重力势能,C错误,D正确。
2.选择不同的水平面作为参考平面,物体在某一位置的重力势能和某一过程中重力势能的改变量( )
A.都具有不同的数值
B.都具有相同的数值
C.前者具有相同数值,后者具有不同数值
D.前者具有不同数值,后者具有相同数值
【解析】选D。根据重力势能的相对性,选不同的参考平面,同一位置的重力势能数值不同,但重力势能的改变量是绝对的,与参考平面无关。
二 功与势能的关系
考查角度1
重力做功与重力势能的关系
【典例1】(多选)
如图所示,物体沿不同的路径从A运动到
B,其中按不同的路径:①有摩擦作用,
②无摩擦作用,③无摩擦,但有其他外力拉它。比较这
三种情况下重力做的功W1、W2、W3,重力势能的变化量ΔEp1、ΔEp2、ΔEp3的关系,以下正确的是
( )
A.W1>W2>W3
B.W1=W2=W3
C.ΔEp1=ΔEp2=ΔEp3
D.ΔEp1<ΔEp2<ΔEp3
【解题探究】(1)三个不同的路径,其初、末位置的
_______相同。
(2)_____做功与_____无关。
高度差
重力
路径
【解析】选B、C。重力做功与路径无关,取决于物体初、末位置,且与物体受不受其他力无关。重力势能的变化量只取决于重力做的功,因此,三种情况下重力做功相同,重力势能的变化量也相同。故B、C正确,A、D错误。
【核心归纳】
1.重力做功与重力势能的比较:
概念
项目
重力做功
重力势能
物理意义
重力对物体做功
由物体与地球的相互作用产生,且由它们之间的相对位置决定的能
表达式
WG=mgΔh
Ep=mgh
概念
项目
重力做功
重力势能
影响大小
的因素
重力mg和初、末位置的高度差Δh
重力mg和相对参考平面的高度h
特 点
只与初、末位置的高度差有关,与路径及参考平面的选择无关
与参考平面的选择有关,同一位置的物体,选择不同的参考平面,其重力势能的值不同
过
程
量
状
态
量
概念
项目
重力做功
重力势能
联 系
重力做功过程是重力势能改变的过程,重力做正功,重力势能减少,重力做负功,重力势能增加,且重力做了多少功,重力势能就改变多少,即WG=Ep1-Ep2=-ΔEp
2.重力做功与重力势能变化关系的理解:
(1)无论物体是否受其他力的作用,无论物体做何种运动,关系式WG=-ΔEp总是成立的。
(2)功是能量转化的量度,重力势能的变化是由重力做功引起的,重力做功的多少是重力势能变化的量度。
【规律方法】判断重力做功正负的方法
(1)根据功的定义式判断:若物体向上运动或有竖直向上的分位移,重力做负功;若物体向下运动或有竖直向下的分位移,重力做正功。
(2)根据重力势能的变化与重力做功的关系判断:由关系式WG=-ΔEp得,重力势能增加,重力一定做负功;重力势能减少,重力一定做正功。
考查角度2
弹力做功与弹性势能的关系
【典例2】在水平
地面上放一个竖直轻弹簧,弹簧上端与一
个质量为m的木块相连,若在木块上再作用
一个竖直向下的力F,使木块缓慢向下移动h,力F做功W1,此时木块再次处于平衡状态,如图所示。求:
(1)在木块下移h的过程中重力势能的减少量。
(2)在木块下移h的过程中弹性势能的增加量。
【解题探究】(1)在木块下移的过程中,弹簧的弹力对
木块做___功,弹簧的弹性势能_____。
(2)木块缓慢下移的含义是:木块始终处于_____状态,
合力为___。
负
增加
平衡
零
【解析】(1)据重力做功与重力势能变化的关系有
ΔEp减=WG=mgh。
(2)据弹力做功与弹性势能变化的关系有
ΔEp增′=-W弹。
又因木块缓慢下移,力F与重力mg的合力与弹力等大、反向,
所以W弹=-W1-WG=-W1-mgh,
所以弹性势能的增量ΔEp增′=W1+mgh。
答案:(1)mgh (2)W1+mgh
【核心归纳】
1.弹性势能的产生及影响因素:
(1)
(2)
2.弹性势能与弹力做功的关系:如图所示,O为弹簧的原长处。
(1)弹力做负功:如物体由O向A运动(压缩)或者由O向A′运动(伸长)时,弹性势能增大,其他形式的能转化为弹性势能。
(2)弹力做正功:如物体由A向O运动或者由A′向O运动时,弹性势能减小,弹性势能转化为其他形式的能。
(3)弹力做功与弹性势能变化的关系:弹性势能的变化量总等于弹力对外做功的负值,表达式为W弹=-ΔEp。
3.弹性势能表达式:
(1)弹簧弹力随形变量x的变化图线及围成面积的意义。
类比v-t图象的面积表示位移,F-x
图象与x轴所围的面积表示弹力的
功,如图所示。
所以当弹簧的位移为x时,弹力做功W弹=-
kx·x=
-
kx2。
(2)弹性势能的大小Ep=-W弹=
kx2。
【过关训练】
1.下列关于重力势能与重力做功的说法正确的是( )
A.重力做功的大小与物体的运动路径有关
B.重力做功的大小与参考平面的选取有关
C.参考平面选取不同,重力势能及重力势能的变化都会
发生变化
D.重力势能增加了2
J,其重力一定做了-2
J的功
【解析】选D。重力做功的大小只与物体运动的初、末位置的高度差有关,与物体的运动路径或参考平面的选取无关,A、B错;重力势能与参考平面的选取有关,重力势能的变化与参考平面的选取无关,C错;根据WG=-ΔEp可知,重力势能增加了2
J,其重力一定做了-2
J的功,D对。
2.(多选)物体在某一运动过程中,重力对它做了40
J的负功,下列说法中正确的是
( )
A.物体的高度一定升高,但动能可能不变
B.物体的重力势能一定减少了40
J
C.物体重力势能的改变量不一定等于40
J
D.物体克服重力做了40
J的功
【解析】选A、D。重力做功与重力势能的变化关系是:重力做正功重力势能减小,重力做负功重力势能增加,且重力做功的数值等于重力势能的变化数值,故重力做负功40
J,则重力势能增加40
J,高度增加,物体克服重力做功40
J。故A、D正确,B、C错误。
3.如图所示,将一木球靠在轻质弹簧上,压缩后松手,弹簧将木球弹出。已知弹出过程弹簧做了40
J的功,小球获得的动能为30
J,则此过程
( )
A.弹簧弹性势能减少10
J
B.弹簧弹性势能减少30
J
C.弹簧弹性势能减少40
J
D.弹簧弹性势能的减少量无法计算
【解析】选C。弹簧弹性势能的变化由弹簧的弹力做功来决定,弹簧弹力做了40
J的功,则弹性势能减少了40
J,选项C正确。
4.关于弹簧的弹性势能,下列说法正确的是
( )
A.当弹簧变长时,它的弹性势能一定增大
B.当弹簧变短时,它的弹性势能一定减小
C.在拉伸长度相同时,k越大的弹簧,它的弹性势能越大
D.弹簧在拉伸时的弹性势能一定大于压缩时的弹性势能
【解析】选C。若弹簧处于压缩状态,当弹簧变长时,弹
簧的弹性势能减小,A错误。若处于压缩状态时,弹簧变
短时,弹簧的弹性势能增大,B错误。由Ep=
kx2知,在
拉伸长度相同时,k越大的弹簧,它的弹性势能越大,C正
确。弹簧的弹性势能与弹簧的形变量有关,弹簧在拉伸
时的弹性势能不一定大于压缩时的弹性势能,故D错误。
【拓展例题】考查内容:重力势能变化的求解
【典例示范】如图所示,两个底面积都
是S的圆筒,用一根带有阀门的细管相
连通,放在水平地面上。两筒内盛有密
度为ρ的水,阀门关闭时两筒液面的高度分别为h1和h2,现将连接两筒的管道阀门打开,让左侧筒中的水缓慢流入右侧筒内,最后两筒液面的高度相同,求在此过程中水的重力势能的变化量。
【正确解答】以部分水为研究对象,如图所示,打开阀
门,当两筒水液面相平时,相当于将图中左侧筒中阴影
部分的水移至图中右侧筒中的上方,这部分水的质量
为:m=
,
重心下降Δh=
,故重力做功:WG=mgΔh=
,重力势能减少了
。
答案:减少
第二节
动能 势能
一、功和能的关系
1.能量:一个物体能够对其他物体_____,则该物体具有能量。
做功
2.功与能的关系:
(1)做功的过程就是_________的过程,做了多少功,就
有多少能量发生转化,所以功是_________的量度。
(2)功和能的单位相同,在国际单位制中,都是______。
能量转化
能量转化
焦(J)
【生活链接】
某物理过程中发生了能量转化,那么能量转化了多少可通过何种思路来求解呢?
提示:功是能量转化的量度,可先求解做功多少,再确定能量转化多少,两者数值相等。
二、动能
1.定义:物体由于_____而具有的_____叫作_____。
2.推导:动能与其质量和速度大小的定量关系。
运动
能量
动能
如图所示,一个质量为m、初速度为v的物体,在水平桌面上运动,因受摩擦阻力f的作用,运动一段位移s后静止下来。(规定初速度方向为正方向)
m(-a)
2(-a)s
3.表达式:Ek=______。
(1)物理意义:物体的动能等于___________与它的
_______________的一半。
(2)动能是__(A.标量 B.矢量),是__(A.过程 B.状
态)量。
4.单位:动能的国际单位是_____,简称焦,用符号J表示。
物体的质量
速度的平方乘积
A
B
焦耳
【思考辨析】
(1)两个物体中,速度大的动能也大。
( )
(2)某物体的速度加倍,它的动能也加倍。
( )
(3)做匀速圆周运动的物体的动能保持不变。
( )
提示:(1)×。动能的表达式为Ek=
mv2,即物体的动能大小由质量和速度大小共同决定,速度大的物体的动能不一定大。
(2)×。由Ek=
mv2知,某物体的速度加倍,它的动能变为原来的4倍。
(3)√。由于匀速圆周运动的线速度大小不变,故由
Ek=
mv2知做匀速圆周运动的物体的动能保持不变。
三、重力势能
1.概念:由物体所处位置的_____决定的能量。
高度
2.重力做的功:
(1)做功表达式:WG=mgh=mgh1-mgh2,式中h指初位置与末
位置的_______;h1、h2分别指_______、_______的高
度。
(2)做功的正负:物体_____时重力做正功;物体被_____
时重力做负功。
高度差
初位置
末位置
下降
举高
(3)做功的特点:物体运动时,重力对它做的功只跟它的
_________________有关,而跟物体运动的_____无关。
起点和终点的位置
路径
3.重力势能:
(1)定义:物体的重力与所处高度的乘积。
(2)大小:表达式:Ep=____;单位:_____,符号:J。
(3)标矢性:重力势能是_____,只有大小,没有方向。
mgh
焦耳
标量
(4)重力做功与重力势能变化的关系。
①表达式:WG=______。
②两种情况:
Ep1-Ep2
减少
增加
4.重力势能的相对性:
(1)参考平面:物体的重力势能总是相对于某一_______
来说的,这个_______叫作参考平面。在参考平面上,物
体的重力势能取作__。
水平面
水平面
0
(2)重力势能的相对性特点。
①选择不同的参考平面,物体重力势能的数值是_____
的。
②对选定的参考平面,上方物体的重力势能是___值,下
方物体的重力势能是___值,负号表示物体在这个位置具
有的重力势能要比在参考平面上具有的重力势能___。
不同
正
负
小
5.重力势能的系统性:重力势能是由_____和地面上物
体的_________决定的。
地球
相对位置
【思考辨析】
(1)物体的高度只要发生变化,其重力一定做功。
( )
(2)重力做功多少取决于物体的重力和它通过的路程。
( )
(3)重力势能Ep1=2
J,Ep2=-3
J,则Ep1与Ep2方向相反。
( )
(4)同一物体的重力势能Ep1=2
J,Ep2=-3
J,则Ep1>Ep2。
( )
提示:(1)√。无论做什么运动,只要物体的高度发生变化,其重力一定做功。
(2)×。重力做功多少取决于物体的重力大小和它在初、末位置的高度差。
(3)×。重力势能是标量,没有方向。
(4)√。重力势能为正值,表示物体处于参考平面的上方,为负值表示物体处于参考平面的下方,而同一物体在越高的地方重力势能越大。
四、弹性势能
1.定义:物体由于_________而具有的能量。
2.大小:跟_____的大小有关,_______越大,弹性势能也
越大。对于弹簧来说,弹性势能与_______________有
关。
3.势能:与相互作用物体的_________有关的能量。
发生形变
形变
形变量
拉伸或压缩长度
相对位置
【生活链接】
运动员将箭射出瞬间,弓要恢复原状,此过程中弓的弹性势能怎么变化?
提示:弓的形变量逐渐减小,弹性势能减小。
一 动能、重力势能的理解
考查角度1
动能的理解
【典例1】质量为2
kg的物体A以
5
m/s的速度向北运动,另一个质量为0.5
kg的物体B以
10
m/s的速度向西运动,则下列说法正确的是
( )
A.EkA=EkB
B.EkA>EkB
C.EkA
【解题探究】(1)动能为______(A.标量,B.矢量)。?
(2)动能的大小与速度的方向______(A.有,B.无)关。?
A
B
【解析】选A。根据Ek=
mv2知,EkA=25
J,EkB=25
J,而且动能是标量,所以EkA=EkB,A项正确。
【核心归纳】
(1)动能为状态量,只有正值,与速度的方向无关。
(2)由于速度具有相对性,所以动能也具有相对性。
(3)高中阶段通常取地面为参考系,讨论物体的速度和动能。
考查角度2
重力势能的理解
【典例2】一根粗细均匀的长直铁棒重①600
N,平放在水平地面上。现将一端从地面抬高0.50
m,
而另一端仍在地面上②,则
( )
A.铁棒的重力势能增加了300
J
B.铁棒的重力势能增加了150
J
C.铁棒的重力势能增加量为0
D.铁棒重力势能增加多少与参考平面选取有关,所以无法确定
【审题关键】
序号
信息提取
①
重心在棒的中点上
②
重心升高0.25
m
【解析】选B。铁棒的重心升高的高度h=0.25
m,铁棒增加的重力势能等于克服重力做的功,与参考平面选取无关,即ΔEp=mgh=600×0.25
J=150
J,故B正确。
【核心归纳】
1.重力势能的三性:
(1)标量性:重力势能是标量,只有大小,没有方向,但有正负。重力势能正负的含义:正、负值分别表示物体处于参考平面上方和下方。
(2)相对性:表达式Ep=mgh中的h是相对于参考平面的高度,故重力势能也具有相对性。计算重力势能时必须要选取参考平面,处于参考平面上的任何物体的重力势能都为零。
(3)系统性:重力是地球对物体的吸引而产生的,如果没有地球对物体的吸引,就不会有重力,也不存在重力势能,所以重力势能是这个系统共同具有的。平时所说的“物体的重力势能”只是一种简化的说法。
2.重力势能变化的绝对性:物体在两个高度不同的位置时,由于高度差一定,重力势能之差也是一定的,即物体的重力势能的变化与参考平面的选取无关。
【特别提醒】
(1)零势能面的选择是任意的,在实际应用中,应以解决问题方便为原则选择零势能面。
(2)如果在同一个问题中涉及多个物体的重力势能时,必须选取一个统一的参考平面。
(3)重力势能的正负表示重力势能的大小,正的总比负的大,如2
J>-5
J。
【过关训练】
1.(多选)改变汽车的质量和速度,都能使汽车的动能发生变化,则下列说法中正确的是
( )
A.质量不变,速度增大到原来的2倍,动能增大为原来的2倍
B.速度不变,质量增大到原来的2倍,动能增大为原来的2倍
C.质量减半,速度增大到原来的4倍,动能增大为原来的2倍
D.速度减半,质量增大到原来的4倍,动能不变
【解析】选B、D。动能Ek=
mv2,所以质量m不变,速度
v增大为原来的2倍时,动能Ek增大为原来的4倍,A错误;
速度不变,质量m增大为原来的2倍,则动能Ek也增大为
原来的2倍,B正确;若质量减半,速度增大为原来的4倍,
则动能增大为原来的8倍,C错误;速度v减半,质量增大
为原来的4倍,则Ek′=
×4m
=
mv2=Ek,即动能不
变,D正确。
2.如图所示,桌面距地面0.8
m,一物体质量为2
kg,放在距桌面0.4
m的支架上(g取10
m/s2)。以地面为参考平面,计算物体具有的重力势能,并计算物体由支架下落到桌面的过程中,重力势能减少了多少?
【解析】以地面为参考平面,物体的高度为:
h1=1.2
m。
物体的重力势能为:
Ep1=mgh1=2×10×1.2
J=24
J
物体落至桌面时的高度h2=0.8
m,重力势能为:
Ep2=mgh2=2×10×0.8
J=16
J
物体重力势能的减少量为:
ΔEp=Ep1-Ep2=(24-16)
J=8
J。
答案:24
J 8
J
【补偿训练】
1.关于重力势能的说法正确的是
( )
A.重力势能由重物本身因素决定
B.因为重力势能有负值,所以说重力势能是矢量
C.重力做功才有重力势能,重力不做功,物体就不具有重力势能
D.重力做功引起重力势能变化
【解析】选D。重力势能与重物的重量、高度等有关,A错误。重力势能是标量,其负值表示重物高度低于零势能面,B错误。重力做功时重力势能发生改变,但不做功时物体也具有重力势能,C错误,D正确。
2.选择不同的水平面作为参考平面,物体在某一位置的重力势能和某一过程中重力势能的改变量( )
A.都具有不同的数值
B.都具有相同的数值
C.前者具有相同数值,后者具有不同数值
D.前者具有不同数值,后者具有相同数值
【解析】选D。根据重力势能的相对性,选不同的参考平面,同一位置的重力势能数值不同,但重力势能的改变量是绝对的,与参考平面无关。
二 功与势能的关系
考查角度1
重力做功与重力势能的关系
【典例1】(多选)
如图所示,物体沿不同的路径从A运动到
B,其中按不同的路径:①有摩擦作用,
②无摩擦作用,③无摩擦,但有其他外力拉它。比较这
三种情况下重力做的功W1、W2、W3,重力势能的变化量ΔEp1、ΔEp2、ΔEp3的关系,以下正确的是
( )
A.W1>W2>W3
B.W1=W2=W3
C.ΔEp1=ΔEp2=ΔEp3
D.ΔEp1<ΔEp2<ΔEp3
【解题探究】(1)三个不同的路径,其初、末位置的
_______相同。
(2)_____做功与_____无关。
高度差
重力
路径
【解析】选B、C。重力做功与路径无关,取决于物体初、末位置,且与物体受不受其他力无关。重力势能的变化量只取决于重力做的功,因此,三种情况下重力做功相同,重力势能的变化量也相同。故B、C正确,A、D错误。
【核心归纳】
1.重力做功与重力势能的比较:
概念
项目
重力做功
重力势能
物理意义
重力对物体做功
由物体与地球的相互作用产生,且由它们之间的相对位置决定的能
表达式
WG=mgΔh
Ep=mgh
概念
项目
重力做功
重力势能
影响大小
的因素
重力mg和初、末位置的高度差Δh
重力mg和相对参考平面的高度h
特 点
只与初、末位置的高度差有关,与路径及参考平面的选择无关
与参考平面的选择有关,同一位置的物体,选择不同的参考平面,其重力势能的值不同
过
程
量
状
态
量
概念
项目
重力做功
重力势能
联 系
重力做功过程是重力势能改变的过程,重力做正功,重力势能减少,重力做负功,重力势能增加,且重力做了多少功,重力势能就改变多少,即WG=Ep1-Ep2=-ΔEp
2.重力做功与重力势能变化关系的理解:
(1)无论物体是否受其他力的作用,无论物体做何种运动,关系式WG=-ΔEp总是成立的。
(2)功是能量转化的量度,重力势能的变化是由重力做功引起的,重力做功的多少是重力势能变化的量度。
【规律方法】判断重力做功正负的方法
(1)根据功的定义式判断:若物体向上运动或有竖直向上的分位移,重力做负功;若物体向下运动或有竖直向下的分位移,重力做正功。
(2)根据重力势能的变化与重力做功的关系判断:由关系式WG=-ΔEp得,重力势能增加,重力一定做负功;重力势能减少,重力一定做正功。
考查角度2
弹力做功与弹性势能的关系
【典例2】在水平
地面上放一个竖直轻弹簧,弹簧上端与一
个质量为m的木块相连,若在木块上再作用
一个竖直向下的力F,使木块缓慢向下移动h,力F做功W1,此时木块再次处于平衡状态,如图所示。求:
(1)在木块下移h的过程中重力势能的减少量。
(2)在木块下移h的过程中弹性势能的增加量。
【解题探究】(1)在木块下移的过程中,弹簧的弹力对
木块做___功,弹簧的弹性势能_____。
(2)木块缓慢下移的含义是:木块始终处于_____状态,
合力为___。
负
增加
平衡
零
【解析】(1)据重力做功与重力势能变化的关系有
ΔEp减=WG=mgh。
(2)据弹力做功与弹性势能变化的关系有
ΔEp增′=-W弹。
又因木块缓慢下移,力F与重力mg的合力与弹力等大、反向,
所以W弹=-W1-WG=-W1-mgh,
所以弹性势能的增量ΔEp增′=W1+mgh。
答案:(1)mgh (2)W1+mgh
【核心归纳】
1.弹性势能的产生及影响因素:
(1)
(2)
2.弹性势能与弹力做功的关系:如图所示,O为弹簧的原长处。
(1)弹力做负功:如物体由O向A运动(压缩)或者由O向A′运动(伸长)时,弹性势能增大,其他形式的能转化为弹性势能。
(2)弹力做正功:如物体由A向O运动或者由A′向O运动时,弹性势能减小,弹性势能转化为其他形式的能。
(3)弹力做功与弹性势能变化的关系:弹性势能的变化量总等于弹力对外做功的负值,表达式为W弹=-ΔEp。
3.弹性势能表达式:
(1)弹簧弹力随形变量x的变化图线及围成面积的意义。
类比v-t图象的面积表示位移,F-x
图象与x轴所围的面积表示弹力的
功,如图所示。
所以当弹簧的位移为x时,弹力做功W弹=-
kx·x=
-
kx2。
(2)弹性势能的大小Ep=-W弹=
kx2。
【过关训练】
1.下列关于重力势能与重力做功的说法正确的是( )
A.重力做功的大小与物体的运动路径有关
B.重力做功的大小与参考平面的选取有关
C.参考平面选取不同,重力势能及重力势能的变化都会
发生变化
D.重力势能增加了2
J,其重力一定做了-2
J的功
【解析】选D。重力做功的大小只与物体运动的初、末位置的高度差有关,与物体的运动路径或参考平面的选取无关,A、B错;重力势能与参考平面的选取有关,重力势能的变化与参考平面的选取无关,C错;根据WG=-ΔEp可知,重力势能增加了2
J,其重力一定做了-2
J的功,D对。
2.(多选)物体在某一运动过程中,重力对它做了40
J的负功,下列说法中正确的是
( )
A.物体的高度一定升高,但动能可能不变
B.物体的重力势能一定减少了40
J
C.物体重力势能的改变量不一定等于40
J
D.物体克服重力做了40
J的功
【解析】选A、D。重力做功与重力势能的变化关系是:重力做正功重力势能减小,重力做负功重力势能增加,且重力做功的数值等于重力势能的变化数值,故重力做负功40
J,则重力势能增加40
J,高度增加,物体克服重力做功40
J。故A、D正确,B、C错误。
3.如图所示,将一木球靠在轻质弹簧上,压缩后松手,弹簧将木球弹出。已知弹出过程弹簧做了40
J的功,小球获得的动能为30
J,则此过程
( )
A.弹簧弹性势能减少10
J
B.弹簧弹性势能减少30
J
C.弹簧弹性势能减少40
J
D.弹簧弹性势能的减少量无法计算
【解析】选C。弹簧弹性势能的变化由弹簧的弹力做功来决定,弹簧弹力做了40
J的功,则弹性势能减少了40
J,选项C正确。
4.关于弹簧的弹性势能,下列说法正确的是
( )
A.当弹簧变长时,它的弹性势能一定增大
B.当弹簧变短时,它的弹性势能一定减小
C.在拉伸长度相同时,k越大的弹簧,它的弹性势能越大
D.弹簧在拉伸时的弹性势能一定大于压缩时的弹性势能
【解析】选C。若弹簧处于压缩状态,当弹簧变长时,弹
簧的弹性势能减小,A错误。若处于压缩状态时,弹簧变
短时,弹簧的弹性势能增大,B错误。由Ep=
kx2知,在
拉伸长度相同时,k越大的弹簧,它的弹性势能越大,C正
确。弹簧的弹性势能与弹簧的形变量有关,弹簧在拉伸
时的弹性势能不一定大于压缩时的弹性势能,故D错误。
【拓展例题】考查内容:重力势能变化的求解
【典例示范】如图所示,两个底面积都
是S的圆筒,用一根带有阀门的细管相
连通,放在水平地面上。两筒内盛有密
度为ρ的水,阀门关闭时两筒液面的高度分别为h1和h2,现将连接两筒的管道阀门打开,让左侧筒中的水缓慢流入右侧筒内,最后两筒液面的高度相同,求在此过程中水的重力势能的变化量。
【正确解答】以部分水为研究对象,如图所示,打开阀
门,当两筒水液面相平时,相当于将图中左侧筒中阴影
部分的水移至图中右侧筒中的上方,这部分水的质量
为:m=
,
重心下降Δh=
,故重力做功:WG=mgΔh=
,重力势能减少了
。
答案:减少
同课章节目录
- 第一章 抛体运动
- 第01节 什么是抛体运动
- 第02节 运动的合成与分解
- 第03节 竖直方向的抛体运动
- 第04节 平抛运动
- 第05节 斜抛运动
- 第二章 圆周运动
- 第01节 匀速圆周运动
- 第02节 向心力
- 第03节 离心现象及其应用
- 第三章 万有引力定律及其应用
- 第01节 万有引力定律
- 第02节 万有引力定律的应用
- 第03节 飞向太空
- 第四章 机械能和能源
- 第01节 功
- 第02节 动能 势能
- 第03节 探究外力做功与物体动能变化的关系
- 第04节 机械能守恒定律
- 第05节 验证机械能守恒定律
- 第06节 能量 能量转化与守恒定律
- 第07节 功率
- 第08节 能源的开发与利用
- 第五章 经典力学与物理学的革命
- 第01节 经典力学的成就与局限性
- 第02节 经典时空观与相对论时空观
- 第03节 量子化现象
- 第04节 物理学——人类文明进步的阶梯
