五年级数学下册试题 一课一练2.1《长方体的认识》习题 -北师大版(含答案)
文档属性
| 名称 | 五年级数学下册试题 一课一练2.1《长方体的认识》习题 -北师大版(含答案) | 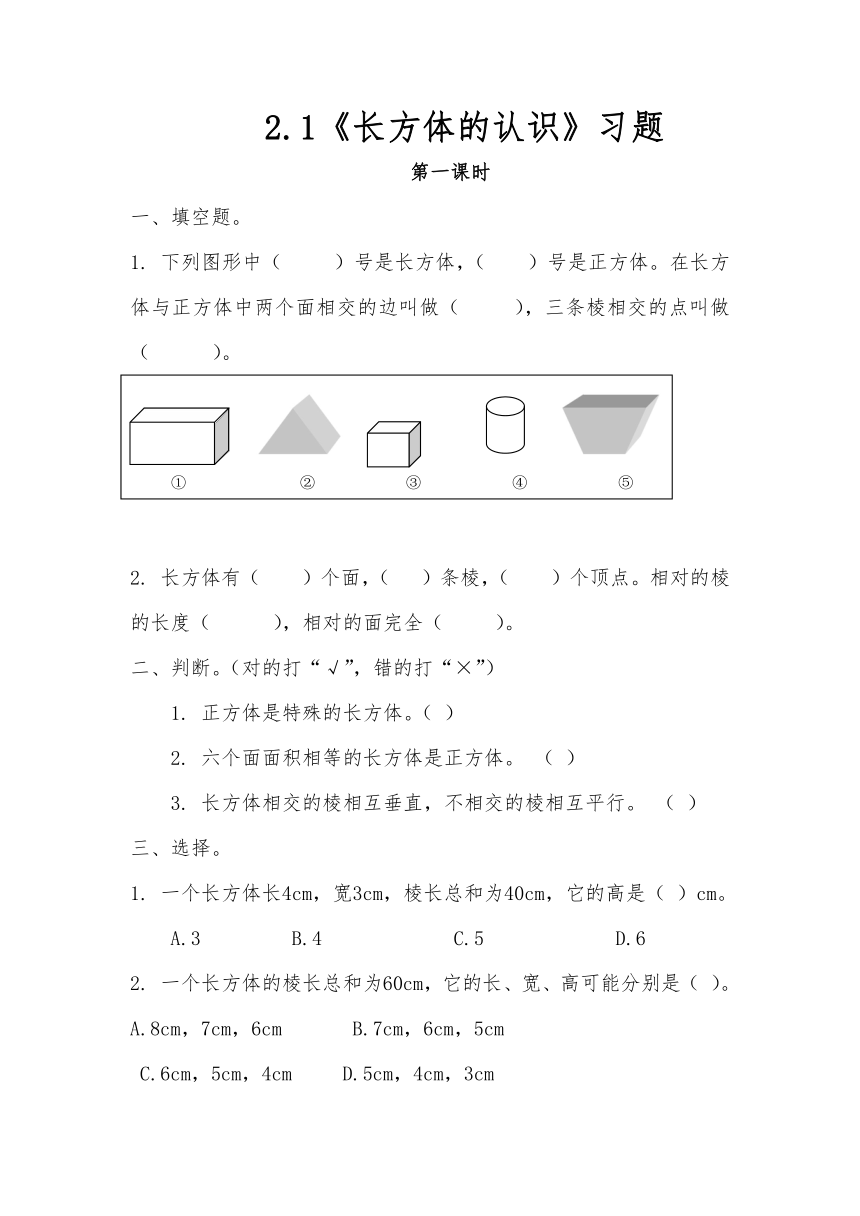 | |
| 格式 | zip | ||
| 文件大小 | 88.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-10 07:21:39 | ||
图片预览



文档简介
2.1《长方体的认识》习题
第一课时
一、填空题。
1.
下列图形中(
)号是长方体,(
)号是正方体。在长方体与正方体中两个面相交的边叫做(
),三条棱相交的点叫做(
)。
2.
长方体有(
)个面,(
)条棱,(
)个顶点。相对的棱的长度(
),相对的面完全(
)。
二、判断。(对的打“√”,错的打“×”)
1.
正方体是特殊的长方体。(
)
2.
六个面面积相等的长方体是正方体。
(
)
3.
长方体相交的棱相互垂直,不相交的棱相互平行。
(
)
三、选择。
1.
一个长方体长4cm,宽3cm,棱长总和为40cm,它的高是(
)cm。
A.3
B.4
C.5
D.6
2.
一个长方体的棱长总和为60cm,它的长、宽、高可能分别是(
)。
A.8cm,7cm,6cm
B.7cm,6cm,5cm
C.6cm,5cm,4cm
D.5cm,4cm,3cm
3.
用八个棱长相等的小正方体拼成一个新的大正方体,它们的表面积减少了(
),棱长之和减少了(
)。
A.
B.
C.
D.
四、应用。
1.
一个正方体的棱长总和是60cm,则它一个面的面积是多少cm2
?
2.
小丽想用12
个棱长为1cm
的小正方体摆成不同的长方体,可以有几种不同的摆法?
3.
将一个棱长为4cm
的正方体切成两个长方体,这两个长方体的总面积为多少cm2
?
第二课时
1.填一填。
(1)长方体有(
)个面,(
)条棱,(
)个顶点,长方体两个面相交的边叫作(
)。
(2)在一个长方体的顶点上相交了(
)条棱,这三条棱的长度分别叫作长方体的(
)、(
)、(
)。
2.指出长方体的长、宽、高分别是多少,并且计算出指定面的面积。
长:______
宽:______
高:_______
上面:_____________________
左面:________________________
前面:_________________________
3.正方体有(
)个面,每个面都是(
)形,每个面的面积(
),每条棱的长度(
),正方体是(
)的长方体。
4.指出正方体的棱长是多少,并且计算出棱长总和与一个面的面积。(单位:厘米)
棱长:__________________
棱长总和:_____________________
一个面的面积:___________________
5.判一判。(对的画“√”,错的画“×”)
(l)长方体可能有两个相对的面是正方形。
(
)
(2)一个长方体(非正方体)中可能有4个面是正方形。(
)[
(3)长方体(非正方体)中相邻两个面的面积相等。
(
)
(4)一个正方体的棱长是2厘米,它的棱长总和是24厘米。(
)
6.选一选。(将正确答案的序号填在括号里)
下列图形中(
)号是长方体,(
)号是正方体。在长方体与正方体中两个面相交的边叫做(
),三条棱相交的点叫做(
)。
[
7.做一个长12厘米,宽10厘米,高2分米的长方体木质框架,需要多少厘米木条?
第一课时答案
一、1.①
③
棱
顶点
2.6
12
8
相等
相同
二、1.
√
2.
√
3.
×
三、1.A
2.C
3.B
D
四、解题步骤仅供参考
1.
解:60÷12
=
5cm
5×5
=
25cm2
答:这个正方体一个面面积为25cm2。
2.
解:因为1×1×12=
12;1×2×6
=
12;2×2×3
=
12;1×3×4
=
12。
所以可以摆成四种长方体,第一种三条棱长分别为1cm,1cm,12cm;第二种三条棱长分别为1cm,2cm,6cm;第三种三条棱长分别为2cm,2cm,3cm;第四种三条棱长分别为1cm,3cm,4cm。
3.
解:正方体的面积为4×4×6
=
96cm2
切成两半后,面积增加了4×4×2
=
32cm2
两个长方体总面积为96
+
32=128cm2。
答:两个长方体总面积为128cm2。
第二课时答案
1.(1)6
12
8棱(2)3长宽高
2.7
cm
5
cm
3
cm
5×7=35(Cm2)
3×7=2I(Cm2)
5×3=15(cm2)
3.6正方都相等都相等特殊
4.7厘米12×7=84(厘米)7×7=49(厘米2)
5.(1)√
(2)×
(3)×
(4)√
6.①③棱顶点
7.2分米=20厘米12X4+10X4+20×4=168(厘米)
第一课时
一、填空题。
1.
下列图形中(
)号是长方体,(
)号是正方体。在长方体与正方体中两个面相交的边叫做(
),三条棱相交的点叫做(
)。
2.
长方体有(
)个面,(
)条棱,(
)个顶点。相对的棱的长度(
),相对的面完全(
)。
二、判断。(对的打“√”,错的打“×”)
1.
正方体是特殊的长方体。(
)
2.
六个面面积相等的长方体是正方体。
(
)
3.
长方体相交的棱相互垂直,不相交的棱相互平行。
(
)
三、选择。
1.
一个长方体长4cm,宽3cm,棱长总和为40cm,它的高是(
)cm。
A.3
B.4
C.5
D.6
2.
一个长方体的棱长总和为60cm,它的长、宽、高可能分别是(
)。
A.8cm,7cm,6cm
B.7cm,6cm,5cm
C.6cm,5cm,4cm
D.5cm,4cm,3cm
3.
用八个棱长相等的小正方体拼成一个新的大正方体,它们的表面积减少了(
),棱长之和减少了(
)。
A.
B.
C.
D.
四、应用。
1.
一个正方体的棱长总和是60cm,则它一个面的面积是多少cm2
?
2.
小丽想用12
个棱长为1cm
的小正方体摆成不同的长方体,可以有几种不同的摆法?
3.
将一个棱长为4cm
的正方体切成两个长方体,这两个长方体的总面积为多少cm2
?
第二课时
1.填一填。
(1)长方体有(
)个面,(
)条棱,(
)个顶点,长方体两个面相交的边叫作(
)。
(2)在一个长方体的顶点上相交了(
)条棱,这三条棱的长度分别叫作长方体的(
)、(
)、(
)。
2.指出长方体的长、宽、高分别是多少,并且计算出指定面的面积。
长:______
宽:______
高:_______
上面:_____________________
左面:________________________
前面:_________________________
3.正方体有(
)个面,每个面都是(
)形,每个面的面积(
),每条棱的长度(
),正方体是(
)的长方体。
4.指出正方体的棱长是多少,并且计算出棱长总和与一个面的面积。(单位:厘米)
棱长:__________________
棱长总和:_____________________
一个面的面积:___________________
5.判一判。(对的画“√”,错的画“×”)
(l)长方体可能有两个相对的面是正方形。
(
)
(2)一个长方体(非正方体)中可能有4个面是正方形。(
)[
(3)长方体(非正方体)中相邻两个面的面积相等。
(
)
(4)一个正方体的棱长是2厘米,它的棱长总和是24厘米。(
)
6.选一选。(将正确答案的序号填在括号里)
下列图形中(
)号是长方体,(
)号是正方体。在长方体与正方体中两个面相交的边叫做(
),三条棱相交的点叫做(
)。
[
7.做一个长12厘米,宽10厘米,高2分米的长方体木质框架,需要多少厘米木条?
第一课时答案
一、1.①
③
棱
顶点
2.6
12
8
相等
相同
二、1.
√
2.
√
3.
×
三、1.A
2.C
3.B
D
四、解题步骤仅供参考
1.
解:60÷12
=
5cm
5×5
=
25cm2
答:这个正方体一个面面积为25cm2。
2.
解:因为1×1×12=
12;1×2×6
=
12;2×2×3
=
12;1×3×4
=
12。
所以可以摆成四种长方体,第一种三条棱长分别为1cm,1cm,12cm;第二种三条棱长分别为1cm,2cm,6cm;第三种三条棱长分别为2cm,2cm,3cm;第四种三条棱长分别为1cm,3cm,4cm。
3.
解:正方体的面积为4×4×6
=
96cm2
切成两半后,面积增加了4×4×2
=
32cm2
两个长方体总面积为96
+
32=128cm2。
答:两个长方体总面积为128cm2。
第二课时答案
1.(1)6
12
8棱(2)3长宽高
2.7
cm
5
cm
3
cm
5×7=35(Cm2)
3×7=2I(Cm2)
5×3=15(cm2)
3.6正方都相等都相等特殊
4.7厘米12×7=84(厘米)7×7=49(厘米2)
5.(1)√
(2)×
(3)×
(4)√
6.①③棱顶点
7.2分米=20厘米12X4+10X4+20×4=168(厘米)
