广州市白云中学2019-2020学年高中物理粤教版选修3-4:1.5用单摆测定重力加速度 同步练习(含解析)
文档属性
| 名称 | 广州市白云中学2019-2020学年高中物理粤教版选修3-4:1.5用单摆测定重力加速度 同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 319.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-07-10 10:14:00 | ||
图片预览




文档简介
1.5用单摆测定重力加速度
1.用单摆测定重力加速度的实验装置如下图所示。
(1)组装单摆时,应在下列器材中选用__________(选填选项前的字母)。
A.长度为1
m左右的细线
B.长度为30
cm左右的细线
C.直径为1.8
cm的塑料球
D.直径为1.8
cm的铁球
(2)测出悬点O到小球球心的距离(摆长)L及单摆完成n次全振动所用的时间t,则重力加速度g=_______(用L、n、t表示)。
(3)下表是某同学记录的乙组实验数据,并做了部分计算处理。
组次
1
2
3
摆长L/cm
80.00
90.00
100.00
50次全振动所用的时间t/s
90.0
95.5
100.5
振动周期T/s
1.80
1.91
重力加速度g/(ms-2)
9.74
9.73
请计算出第3组实验中的T=________s,g=___________。
(4)用多组实验数据做出图像,也可以求出重力加速度g,已知三位同学做出的图线的示意图如下图中的a、b、c所示,其中a和b平行,b和c都过原点,图线b对应的g值最接近当地重力加速度的值。则相对于图线b,下列分析正确的是_________(选填选项前的字母)。
A.出现图线a的原因可能是误将悬点到小球下端的距离记为摆长L
B.出现图线c的原因可能是误将49次全振动记为50次
C.图线c对应的g值小于图线b对应的g值
(5)某同学在家里测重力加速度。他找到细线和铁锁,制成一个单摆,如下图所示,由于家里只有一根量程为30
cm的刻度尺,于是他在细线上的A点做了一个标记,使得悬点O到A点间的细线长度小于刻度尺量程。保持该标记以下的细线长度不变,通过改变O、A间细线长度以改变摆长。实验中,当O、A间细线的长度分别为和时,测得相应单摆的周期为、。由此可得重力加速度g=__________(用、、、表示)。
2.在“用单摆测定重力加速度”的实验中,测得单摆摆角小于5°,完成n次全振动的时间为t,用毫米刻度尺测得摆线长为L,用游标卡尺测得摆球直径为d:
(1)用上述物理量的符号写出重力加速度的一般表达式g=_______________;
(2)从下图可知,摆球直径d的读数为__________cm;
(3)实验中有个同学发现他测得重力加速度的值偏大,其原因可能是__________。
A.以摆线长为摆长来计算
B.单摆所用摆球质量太大
C.把n次全振动时间误当成(n+1)次全振动时间
D.悬点未固定紧,振动中出现松动,使摆线增长了
3.在“用单摆测定重力加速度”的实验中:
(1)在做“用单摆测定重力加速度”的实验中,下列措施对提高测量结果精确度有利的是_________。
A.适当加长摆线
B.质量相同、体积不同的摆球,应选用体积较大的
C.多测几组数据,借助T
2-L图像求重力加速度g
D.为便于观察和计数,应在释放摆球的同时开始计时
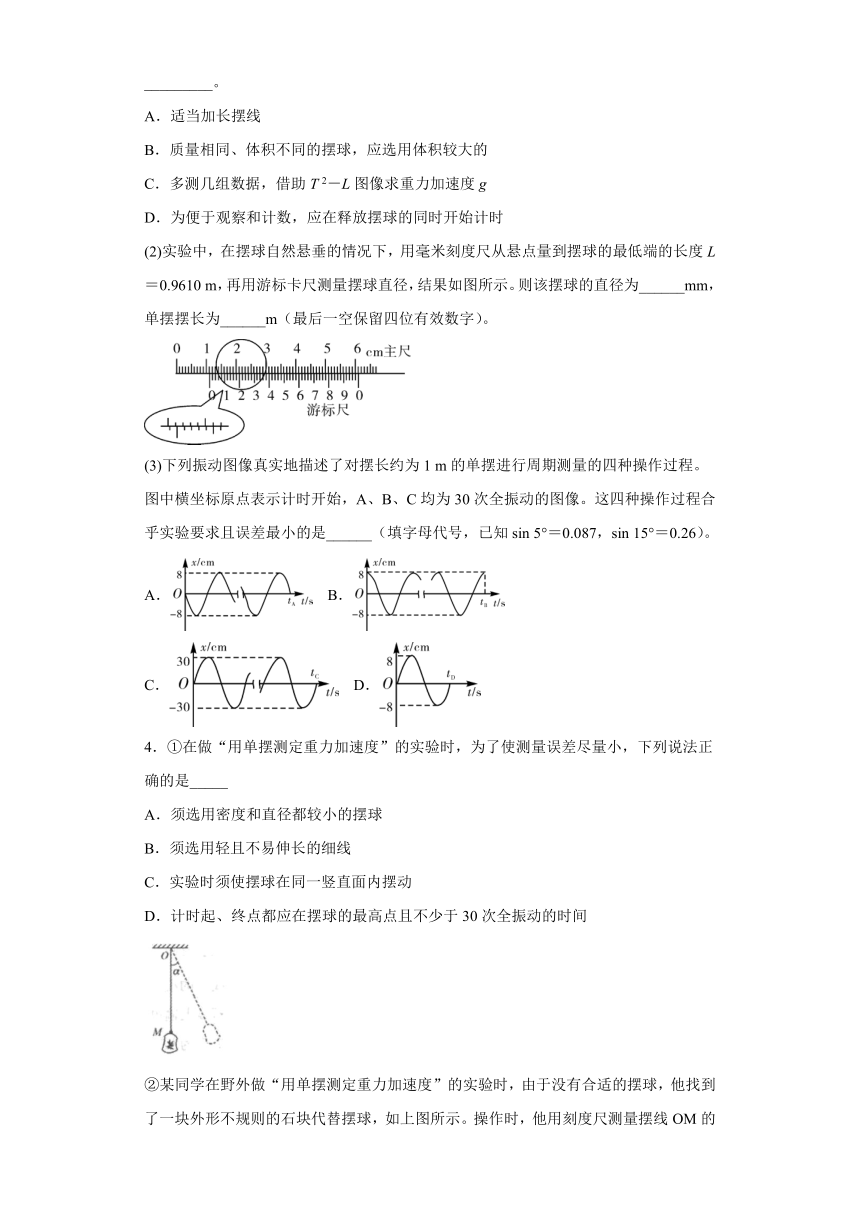
(2)实验中,在摆球自然悬垂的情况下,用毫米刻度尺从悬点量到摆球的最低端的长度L=0.9610
m,再用游标卡尺测量摆球直径,结果如图所示。则该摆球的直径为______mm,单摆摆长为______m(最后一空保留四位有效数字)。
(3)下列振动图像真实地描述了对摆长约为1
m的单摆进行周期测量的四种操作过程。图中横坐标原点表示计时开始,A、B、C均为30次全振动的图像。这四种操作过程合乎实验要求且误差最小的是______(填字母代号,已知sin
5°=0.087,sin
15°=0.26)。
A.
B.
C.
D.
4.①在做“用单摆测定重力加速度”的实验时,为了使测量误差尽量小,下列说法正确的是_____
A.须选用密度和直径都较小的摆球
B.须选用轻且不易伸长的细线
C.实验时须使摆球在同一竖直面内摆动
D.计时起、终点都应在摆球的最高点且不少于30次全振动的时间
②某同学在野外做“用单摆测定重力加速度”的实验时,由于没有合适的摆球,他找到了一块外形不规则的石块代替摆球,如上图所示。操作时,他用刻度尺测量摆线OM的长度L作为摆长,测出n次全振动的总时间由到周期T,求出重力加速度,这样得到的重力加速度的测量值比真实值_____(填“大”或“小”)。为了克服摆长无法准确测量的困难,该同学将摆线长度缩短为,重复上面的实验,得出周期,由此他得到了较精确的重力加速度值g=_____。
5.用单摆测定重力加速度g的实验。如图,甲、乙、丙分别是三位同学做出的单摆周期平方与摆长的T2-L图线。其中甲、乙平行,乙、丙均过原点,根据乙求出的g值接近当地重力加速度的值,则下列分析正确的是( )
A.根据甲求出的g值大于根据乙求出的g值
B.根据丙求出的g值大于根据乙求出的g值
C.根据T2-L图线,可以由g求出g的值
D.甲不过原点的原因可能是误将悬点到摆球上端的距离记为摆长L
E.丙偏离乙的原因可能是记录时误将摆球经过平衡位置的次数当成全振动的次数
6.用单摆测定重力加速度的实验装置如图所示。
(1)组装单摆时,应在下列器材中选用________(选填选项前的字母).
A.长度为1m左右的细线
B.长度为30cm左右的细线
C.直径为1.8cm的塑料球
D.直径为1.8cm的铁球
(2)测出悬点O到小球球心的距离(摆长)L及单摆完成n次全振动所用的时间t,则重力加速度g=__________(用L、n、t表示).
(3)下表是某同学记录的3组实验数据,并做了部分计算处理.
请计算出第3组实验中的T=________s,g=________m/s2.
7.在做“用单摆测定重力加速度”的实验过程中:
(1)小李同学用游标卡尺测得摆球的直径如图所示,则摆球直径d=________cm。
(2)小张同学实验时却不小心忘记测量小球的半径,但测量了两次摆线长和周期,第一次测得悬线长为L1,对应振动周期为T1;第二次测得悬线长为L2,对应单摆的振动周期为T2,根据以上测量数据也可导出重力加速度的表达式为_________________。
8.某实验小组在利用摆长约为1m的单摆测定当地重力加速度的实验中:
(1)周期测量环节进行了下列振动图像所描述的四种操作过程,图中横坐标原点表示计时开始,A、B、C、D均为30次全振动图像,已知sin=0.087,sin=0.259,这四种操作过程合乎实验要求且误差最小的是_____(填字母代号);
A.B.
C.D.
(2)改变摆长,利用测出的多组周期T、摆长L数据,做出T2-L图像,可以更准确求出重力加速度g,已知三位同学做出的T2-L图线的示意图如图中的a、b、c所示,其中a和b平行,b和c都过原点,图线b对应的g值最接近当地重力加速度的值。则相对于图线b,出现图线a的原因可能是摆长L测量值_______(填“偏大”或“偏小”),出现图线c的原因可能是周期T测量值_______(填“偏大”或“偏小”)。
9.在用“单摆测重力加速度”的实验中:
(1)有下列备选器材中,需选用哪些器材较好(_______)
A.长1m左右的粗一点结实棉线
B.长1m左右的细棉线
C.带细孔的直径2cm左右的铁球
D.
带细孔的直径2cm左右的橡胶球
E.时钟
F.秒表
G.学生用刻度尺
H.最小刻度是毫米的米尺
(2)甲同学先用米尺测得摆线长,再用游标卡尺测得摆球直径如图甲所示为_______cm,然后用秒表记录单摆完成50次全振动所用的时间如图乙所示,则单摆的周期为________s(保留三位有效数字)
10.某实验小组利用如图甲所示的装置测量当地的重力加速度。
(1)为了使测量误差尽量小,下列说法中正确的是________;
A.组装单摆须选用密度和直径都较小的摆球
B.组装单摆须选用轻且不易伸长的细线
C.实验时须使摆球在同一竖直面内摆动
D.为了使单摆的周期大一些,应使摆线相距平衡位置有较大的角度
(2)该实验小组用20分度的游标卡尺测量小球的直径。某次测量的示数如图乙所示,读出小球直径为d=______cm;
(3)该同学用米尺测出悬线的长度为L,让小球在竖直平面内摆动。当小球经过最低点时开始计时,并计数为0,此后小球每经过最低点一次,依次计数为1、2、3……。当数到40时,停止计时,测得时间为t。改变悬线长度,多次测量,利用计算机作出了t2–L图线如图丙所示。根据图丙可以得出当地的重力加速度g=__________
m/s2。(取π2=9.86,结果保留3位有效数字)
参考答案
1.AD
2.01
9.76(9.76~9.77)
B
【解析】
根据实验原理,摆长需要在1m左右,小球需要体积较小的实心金属小球;根据单摆的周期公式进行推导各类物理量。
【详解】
(1)[1]在用单摆测定重力加速度的实验基本条件是摆线长度远大于小球直径,小球的密度越大越好;故摆线应选取长约1
m左右的不可伸缩的细线,摆球应选取体积小而质量大的铁球,以减小实验误差,故选AD;
(2)[2]次全振动的时间为,则振动周期为:
根据单摆周期公式:
可推出;
(3)[3]50次全振动的时间为100.5
s,则振动周期为:
[4]代入公式求得:
;
(4)[5]根据单摆的周期公式,可以推导出:
可知图像的斜率,b曲线为正确的图像。斜率越小,对应的重力加速度越大,选项C错误。在图像中图线与纵轴正半轴相交表示计算摆长偏小,如漏加小球半径,与纵轴负半轴相交表示摆长偏大,选项A错误;若误将49次全振动记为50次,则周期测量值偏小,值测量值偏大,对应的图像斜率偏小,故B选项正确。
(5)[6]设A到铁锁重心的距离为,则第一次的实际摆长为,第二次的实际摆长为,由周期公式:
联立消去,解得。
【点睛】
掌握单摆的实验原理,掌握单摆周期的计算公式,进而求解问题。
2.
1.240
C
【解析】
(1)[1]单摆摆角小于5°,摆角足够小,单摆的运动可以看成简谐运动,完成n次全振动的时间为t,则单摆的周期为
小球大小不能忽略,所以摆长是绳长L加上小球的的半径长度,即
由单摆周期公式
联立可解得重力加速度为
(2)[2]游标卡尺的主尺的读数是12mm,游标尺是20分度的,每一小格与标准长度相差
游标尺上第8个刻度与主尺上某一刻度对齐,则游标尺的读数为
则游标尺的读数为
12+0.40mm=12.40mm=1.240cm
(3)[3]由(1)问可知重力加速度为
A.以摆线长作为摆长来计算,则L的测量值偏小,则重力加速度的测量值偏小,故A错误;
B.重力加速度的测量值与摆球质量无关,B错误;
C.把n次全振动时间误当成(n+1)全振动的时间,用的全振动次数多了,即上式中的n大了,导致根据重力加速度的测量值偏大,故C正确;
D.悬点未固定紧,振动中出现松动,使摆线增长了,故L的测量值偏小,则重力加速度的测量值偏小,故D错误。
故选C。
3.AC
11.20
0.9554
A
【解析】
(1)[1]A.单摆的摆长越长,周期越大,适当加长摆长,便于测量周期,可以减小测量的误差,提供测量结果的精确度,故A正确;
B.要减小空气阻力的影响,应选体积较小的摆球,故B错误;
C.多测几组数据,借助T
2-L图象求重力加速度g,能减少偶然误差,故C正确;
D.单摆周期较小,要从经过平衡位置时开始计时,以减小实验的误差,故D错误。
故选AC。
(2)[2]根据游标卡尺的读数规则可知游标卡尺示数为
[3]因为
所以单摆的摆长
(3)[4]当摆角小于等于时,我们认为小球做简谐运动,所以振幅约为
当小球摆到最低点开始计时误差较小,测量周期时要让小球做30~50次全振动,求平均值,所以A合乎实验要求且误差最小,故选A。
4.BC
小
【解析】
(1)
A、为减小空气阻力对实验的影响,从而减小实验误差,组装单摆须选用密度大而直径都较小的摆球,故A错误;
B、为减小实验误差,组装单摆须选用轻且不易伸长的细线,故B正确;
C、实验时须使摆球在同一竖直面内摆动,不能使单摆成为圆锥摆,故C正确;
D、测量时间应从单摆摆到最低点开始,因为最低位置摆球速度最大,相同的视觉距离误差,引起的时间误差较小,则周期测量比较准确,故D错误;
(2)
根据单摆的周期公式得:,该同学用OM的长L作为摆长,摆长偏小,根据上述表达式得知,g的测量值偏小,设摆线的结点到大理石质心的距离为r,则根据单摆的周期公式得:,而,联立解得:。
5.BDE
【解析】
根据单摆的周期公式,得
根据数学知识可知,T2-L图象的斜率
A.由于甲、乙平行即斜率相等,则计算出的加速度相等,故A错误;
B.由图可知,丙的斜率小于乙的斜率,由可知,丙求出的g值大于根据乙求出的g值,故B正确;
C.由可得
则
故C错误;
D.若测量摆长时忘了加上摆球的半径,则摆长变成摆线的长度l,则有
故做出的T2-L图象中a线的原因可能是误将悬点到小球上端的距离记为摆长L,故D正确;
E.记录时误将摆球经过平衡位置的次数当成全振动的次数,则周期的测量值偏小,导致重力加速度的测量值偏大,图线的斜率k偏小,故E正确。
故选BDE。
6.
AD;
;
2.01;
9.76
【解析】(1)为减小实验误差,应选择1m左右的摆线,故选A,为减小空气阻力影响,摆球应选质量大而体积小的金属球,故选D,因此需要的实验器材是AD.
(2)单摆的周期:,由单摆的周期公式:,解得:.
(3)由表中实验数据可知,第三组实验中,周期:.
代入数据得:.
【点睛】解决本题的关键知道实验的原理,以及可以减小误差的方法,掌握单摆的周期公式,知道周期等于完成一次全振动所需的时间,
7.2.030
【解析】
(1)[1]游标卡尺的主尺读数为20mm,游标尺读数为0.05×6mm=0.30mm,则摆球的直径d=20.30mm=2.030cm
(2)[2]设小球的半径为r,根据单摆的周期公式得
T1=2π
T2=2π
联立方程组解得
8.B
偏小
偏小
【解析】
(1)[1]当摆角小于等于时,我们认为小球做单摆运动,所以振幅约为
当小球摆到最低点开始计时,误差较小,测量周期时要让小球做30-50次全振动,求平均值,所以B合乎实验要求且误差最小,ACD错误;
故选B;
(2)[2]根据单摆的周期公式得
根据数学知识可知,T2-L图象的斜率
当地的重力加速度
若测量摆长时忘了加上摆球的半径,则摆长变成摆线的长度l,则有
根据数学知识课知,对T2-L图象来说
与b线
斜率相等,两者应该平行,是截距,故做出T2-L图象中a线的原因可能是误将悬点到小球上端的距离记为摆长L,导致摆长偏小;
(3)[3]对于图中的c线,若周期的测量值T偏小,根据单摆的周期公式得
导致重力加速度的测量值偏大,图线的斜率k偏小。
9.BCFH
0.97
1.50
【解析】
(1)单摆的摆线应该选择长1m左右的细棉线,故选B;摆球选择体积小质量较大的带细孔的直径2cm左右的铁球
,故选C;用秒表记录时间,故选F;另外还要选择最小刻度是毫米的米尺
测量摆长,故选H;
(2)摆球直径为:0.9cm+0.1mm×7=0.97cm;秒表读数为:60s+15.2s=75.2s,则单摆的周期:
10.BC
0.810
9.80
【解析】
(1)[1].A.组装单摆须选用密度较大且直径较小的摆球,选项A错误;
B.组装单摆须选用轻且不易伸长的细线,选项B正确;
C.实验时须使摆球在同一竖直面内摆动,选项C正确;
D.单摆的摆角不得超过5°,否则单摆的运动就不是简谐运动,选项D错误;
故选BC。
(2)[2].小球直径为d=0.8cm+0.05mm×2=0.810cm;
(3)[3].单摆的周期为
由
可得
由图像可知
解得
g=9.80m/s2
1.用单摆测定重力加速度的实验装置如下图所示。
(1)组装单摆时,应在下列器材中选用__________(选填选项前的字母)。
A.长度为1
m左右的细线
B.长度为30
cm左右的细线
C.直径为1.8
cm的塑料球
D.直径为1.8
cm的铁球
(2)测出悬点O到小球球心的距离(摆长)L及单摆完成n次全振动所用的时间t,则重力加速度g=_______(用L、n、t表示)。
(3)下表是某同学记录的乙组实验数据,并做了部分计算处理。
组次
1
2
3
摆长L/cm
80.00
90.00
100.00
50次全振动所用的时间t/s
90.0
95.5
100.5
振动周期T/s
1.80
1.91
重力加速度g/(ms-2)
9.74
9.73
请计算出第3组实验中的T=________s,g=___________。
(4)用多组实验数据做出图像,也可以求出重力加速度g,已知三位同学做出的图线的示意图如下图中的a、b、c所示,其中a和b平行,b和c都过原点,图线b对应的g值最接近当地重力加速度的值。则相对于图线b,下列分析正确的是_________(选填选项前的字母)。
A.出现图线a的原因可能是误将悬点到小球下端的距离记为摆长L
B.出现图线c的原因可能是误将49次全振动记为50次
C.图线c对应的g值小于图线b对应的g值
(5)某同学在家里测重力加速度。他找到细线和铁锁,制成一个单摆,如下图所示,由于家里只有一根量程为30
cm的刻度尺,于是他在细线上的A点做了一个标记,使得悬点O到A点间的细线长度小于刻度尺量程。保持该标记以下的细线长度不变,通过改变O、A间细线长度以改变摆长。实验中,当O、A间细线的长度分别为和时,测得相应单摆的周期为、。由此可得重力加速度g=__________(用、、、表示)。
2.在“用单摆测定重力加速度”的实验中,测得单摆摆角小于5°,完成n次全振动的时间为t,用毫米刻度尺测得摆线长为L,用游标卡尺测得摆球直径为d:
(1)用上述物理量的符号写出重力加速度的一般表达式g=_______________;
(2)从下图可知,摆球直径d的读数为__________cm;
(3)实验中有个同学发现他测得重力加速度的值偏大,其原因可能是__________。
A.以摆线长为摆长来计算
B.单摆所用摆球质量太大
C.把n次全振动时间误当成(n+1)次全振动时间
D.悬点未固定紧,振动中出现松动,使摆线增长了
3.在“用单摆测定重力加速度”的实验中:
(1)在做“用单摆测定重力加速度”的实验中,下列措施对提高测量结果精确度有利的是_________。
A.适当加长摆线
B.质量相同、体积不同的摆球,应选用体积较大的
C.多测几组数据,借助T
2-L图像求重力加速度g
D.为便于观察和计数,应在释放摆球的同时开始计时
(2)实验中,在摆球自然悬垂的情况下,用毫米刻度尺从悬点量到摆球的最低端的长度L=0.9610
m,再用游标卡尺测量摆球直径,结果如图所示。则该摆球的直径为______mm,单摆摆长为______m(最后一空保留四位有效数字)。
(3)下列振动图像真实地描述了对摆长约为1
m的单摆进行周期测量的四种操作过程。图中横坐标原点表示计时开始,A、B、C均为30次全振动的图像。这四种操作过程合乎实验要求且误差最小的是______(填字母代号,已知sin
5°=0.087,sin
15°=0.26)。
A.
B.
C.
D.
4.①在做“用单摆测定重力加速度”的实验时,为了使测量误差尽量小,下列说法正确的是_____
A.须选用密度和直径都较小的摆球
B.须选用轻且不易伸长的细线
C.实验时须使摆球在同一竖直面内摆动
D.计时起、终点都应在摆球的最高点且不少于30次全振动的时间
②某同学在野外做“用单摆测定重力加速度”的实验时,由于没有合适的摆球,他找到了一块外形不规则的石块代替摆球,如上图所示。操作时,他用刻度尺测量摆线OM的长度L作为摆长,测出n次全振动的总时间由到周期T,求出重力加速度,这样得到的重力加速度的测量值比真实值_____(填“大”或“小”)。为了克服摆长无法准确测量的困难,该同学将摆线长度缩短为,重复上面的实验,得出周期,由此他得到了较精确的重力加速度值g=_____。
5.用单摆测定重力加速度g的实验。如图,甲、乙、丙分别是三位同学做出的单摆周期平方与摆长的T2-L图线。其中甲、乙平行,乙、丙均过原点,根据乙求出的g值接近当地重力加速度的值,则下列分析正确的是( )
A.根据甲求出的g值大于根据乙求出的g值
B.根据丙求出的g值大于根据乙求出的g值
C.根据T2-L图线,可以由g求出g的值
D.甲不过原点的原因可能是误将悬点到摆球上端的距离记为摆长L
E.丙偏离乙的原因可能是记录时误将摆球经过平衡位置的次数当成全振动的次数
6.用单摆测定重力加速度的实验装置如图所示。
(1)组装单摆时,应在下列器材中选用________(选填选项前的字母).
A.长度为1m左右的细线
B.长度为30cm左右的细线
C.直径为1.8cm的塑料球
D.直径为1.8cm的铁球
(2)测出悬点O到小球球心的距离(摆长)L及单摆完成n次全振动所用的时间t,则重力加速度g=__________(用L、n、t表示).
(3)下表是某同学记录的3组实验数据,并做了部分计算处理.
请计算出第3组实验中的T=________s,g=________m/s2.
7.在做“用单摆测定重力加速度”的实验过程中:
(1)小李同学用游标卡尺测得摆球的直径如图所示,则摆球直径d=________cm。
(2)小张同学实验时却不小心忘记测量小球的半径,但测量了两次摆线长和周期,第一次测得悬线长为L1,对应振动周期为T1;第二次测得悬线长为L2,对应单摆的振动周期为T2,根据以上测量数据也可导出重力加速度的表达式为_________________。
8.某实验小组在利用摆长约为1m的单摆测定当地重力加速度的实验中:
(1)周期测量环节进行了下列振动图像所描述的四种操作过程,图中横坐标原点表示计时开始,A、B、C、D均为30次全振动图像,已知sin=0.087,sin=0.259,这四种操作过程合乎实验要求且误差最小的是_____(填字母代号);
A.B.
C.D.
(2)改变摆长,利用测出的多组周期T、摆长L数据,做出T2-L图像,可以更准确求出重力加速度g,已知三位同学做出的T2-L图线的示意图如图中的a、b、c所示,其中a和b平行,b和c都过原点,图线b对应的g值最接近当地重力加速度的值。则相对于图线b,出现图线a的原因可能是摆长L测量值_______(填“偏大”或“偏小”),出现图线c的原因可能是周期T测量值_______(填“偏大”或“偏小”)。
9.在用“单摆测重力加速度”的实验中:
(1)有下列备选器材中,需选用哪些器材较好(_______)
A.长1m左右的粗一点结实棉线
B.长1m左右的细棉线
C.带细孔的直径2cm左右的铁球
D.
带细孔的直径2cm左右的橡胶球
E.时钟
F.秒表
G.学生用刻度尺
H.最小刻度是毫米的米尺
(2)甲同学先用米尺测得摆线长,再用游标卡尺测得摆球直径如图甲所示为_______cm,然后用秒表记录单摆完成50次全振动所用的时间如图乙所示,则单摆的周期为________s(保留三位有效数字)
10.某实验小组利用如图甲所示的装置测量当地的重力加速度。
(1)为了使测量误差尽量小,下列说法中正确的是________;
A.组装单摆须选用密度和直径都较小的摆球
B.组装单摆须选用轻且不易伸长的细线
C.实验时须使摆球在同一竖直面内摆动
D.为了使单摆的周期大一些,应使摆线相距平衡位置有较大的角度
(2)该实验小组用20分度的游标卡尺测量小球的直径。某次测量的示数如图乙所示,读出小球直径为d=______cm;
(3)该同学用米尺测出悬线的长度为L,让小球在竖直平面内摆动。当小球经过最低点时开始计时,并计数为0,此后小球每经过最低点一次,依次计数为1、2、3……。当数到40时,停止计时,测得时间为t。改变悬线长度,多次测量,利用计算机作出了t2–L图线如图丙所示。根据图丙可以得出当地的重力加速度g=__________
m/s2。(取π2=9.86,结果保留3位有效数字)
参考答案
1.AD
2.01
9.76(9.76~9.77)
B
【解析】
根据实验原理,摆长需要在1m左右,小球需要体积较小的实心金属小球;根据单摆的周期公式进行推导各类物理量。
【详解】
(1)[1]在用单摆测定重力加速度的实验基本条件是摆线长度远大于小球直径,小球的密度越大越好;故摆线应选取长约1
m左右的不可伸缩的细线,摆球应选取体积小而质量大的铁球,以减小实验误差,故选AD;
(2)[2]次全振动的时间为,则振动周期为:
根据单摆周期公式:
可推出;
(3)[3]50次全振动的时间为100.5
s,则振动周期为:
[4]代入公式求得:
;
(4)[5]根据单摆的周期公式,可以推导出:
可知图像的斜率,b曲线为正确的图像。斜率越小,对应的重力加速度越大,选项C错误。在图像中图线与纵轴正半轴相交表示计算摆长偏小,如漏加小球半径,与纵轴负半轴相交表示摆长偏大,选项A错误;若误将49次全振动记为50次,则周期测量值偏小,值测量值偏大,对应的图像斜率偏小,故B选项正确。
(5)[6]设A到铁锁重心的距离为,则第一次的实际摆长为,第二次的实际摆长为,由周期公式:
联立消去,解得。
【点睛】
掌握单摆的实验原理,掌握单摆周期的计算公式,进而求解问题。
2.
1.240
C
【解析】
(1)[1]单摆摆角小于5°,摆角足够小,单摆的运动可以看成简谐运动,完成n次全振动的时间为t,则单摆的周期为
小球大小不能忽略,所以摆长是绳长L加上小球的的半径长度,即
由单摆周期公式
联立可解得重力加速度为
(2)[2]游标卡尺的主尺的读数是12mm,游标尺是20分度的,每一小格与标准长度相差
游标尺上第8个刻度与主尺上某一刻度对齐,则游标尺的读数为
则游标尺的读数为
12+0.40mm=12.40mm=1.240cm
(3)[3]由(1)问可知重力加速度为
A.以摆线长作为摆长来计算,则L的测量值偏小,则重力加速度的测量值偏小,故A错误;
B.重力加速度的测量值与摆球质量无关,B错误;
C.把n次全振动时间误当成(n+1)全振动的时间,用的全振动次数多了,即上式中的n大了,导致根据重力加速度的测量值偏大,故C正确;
D.悬点未固定紧,振动中出现松动,使摆线增长了,故L的测量值偏小,则重力加速度的测量值偏小,故D错误。
故选C。
3.AC
11.20
0.9554
A
【解析】
(1)[1]A.单摆的摆长越长,周期越大,适当加长摆长,便于测量周期,可以减小测量的误差,提供测量结果的精确度,故A正确;
B.要减小空气阻力的影响,应选体积较小的摆球,故B错误;
C.多测几组数据,借助T
2-L图象求重力加速度g,能减少偶然误差,故C正确;
D.单摆周期较小,要从经过平衡位置时开始计时,以减小实验的误差,故D错误。
故选AC。
(2)[2]根据游标卡尺的读数规则可知游标卡尺示数为
[3]因为
所以单摆的摆长
(3)[4]当摆角小于等于时,我们认为小球做简谐运动,所以振幅约为
当小球摆到最低点开始计时误差较小,测量周期时要让小球做30~50次全振动,求平均值,所以A合乎实验要求且误差最小,故选A。
4.BC
小
【解析】
(1)
A、为减小空气阻力对实验的影响,从而减小实验误差,组装单摆须选用密度大而直径都较小的摆球,故A错误;
B、为减小实验误差,组装单摆须选用轻且不易伸长的细线,故B正确;
C、实验时须使摆球在同一竖直面内摆动,不能使单摆成为圆锥摆,故C正确;
D、测量时间应从单摆摆到最低点开始,因为最低位置摆球速度最大,相同的视觉距离误差,引起的时间误差较小,则周期测量比较准确,故D错误;
(2)
根据单摆的周期公式得:,该同学用OM的长L作为摆长,摆长偏小,根据上述表达式得知,g的测量值偏小,设摆线的结点到大理石质心的距离为r,则根据单摆的周期公式得:,而,联立解得:。
5.BDE
【解析】
根据单摆的周期公式,得
根据数学知识可知,T2-L图象的斜率
A.由于甲、乙平行即斜率相等,则计算出的加速度相等,故A错误;
B.由图可知,丙的斜率小于乙的斜率,由可知,丙求出的g值大于根据乙求出的g值,故B正确;
C.由可得
则
故C错误;
D.若测量摆长时忘了加上摆球的半径,则摆长变成摆线的长度l,则有
故做出的T2-L图象中a线的原因可能是误将悬点到小球上端的距离记为摆长L,故D正确;
E.记录时误将摆球经过平衡位置的次数当成全振动的次数,则周期的测量值偏小,导致重力加速度的测量值偏大,图线的斜率k偏小,故E正确。
故选BDE。
6.
AD;
;
2.01;
9.76
【解析】(1)为减小实验误差,应选择1m左右的摆线,故选A,为减小空气阻力影响,摆球应选质量大而体积小的金属球,故选D,因此需要的实验器材是AD.
(2)单摆的周期:,由单摆的周期公式:,解得:.
(3)由表中实验数据可知,第三组实验中,周期:.
代入数据得:.
【点睛】解决本题的关键知道实验的原理,以及可以减小误差的方法,掌握单摆的周期公式,知道周期等于完成一次全振动所需的时间,
7.2.030
【解析】
(1)[1]游标卡尺的主尺读数为20mm,游标尺读数为0.05×6mm=0.30mm,则摆球的直径d=20.30mm=2.030cm
(2)[2]设小球的半径为r,根据单摆的周期公式得
T1=2π
T2=2π
联立方程组解得
8.B
偏小
偏小
【解析】
(1)[1]当摆角小于等于时,我们认为小球做单摆运动,所以振幅约为
当小球摆到最低点开始计时,误差较小,测量周期时要让小球做30-50次全振动,求平均值,所以B合乎实验要求且误差最小,ACD错误;
故选B;
(2)[2]根据单摆的周期公式得
根据数学知识可知,T2-L图象的斜率
当地的重力加速度
若测量摆长时忘了加上摆球的半径,则摆长变成摆线的长度l,则有
根据数学知识课知,对T2-L图象来说
与b线
斜率相等,两者应该平行,是截距,故做出T2-L图象中a线的原因可能是误将悬点到小球上端的距离记为摆长L,导致摆长偏小;
(3)[3]对于图中的c线,若周期的测量值T偏小,根据单摆的周期公式得
导致重力加速度的测量值偏大,图线的斜率k偏小。
9.BCFH
0.97
1.50
【解析】
(1)单摆的摆线应该选择长1m左右的细棉线,故选B;摆球选择体积小质量较大的带细孔的直径2cm左右的铁球
,故选C;用秒表记录时间,故选F;另外还要选择最小刻度是毫米的米尺
测量摆长,故选H;
(2)摆球直径为:0.9cm+0.1mm×7=0.97cm;秒表读数为:60s+15.2s=75.2s,则单摆的周期:
10.BC
0.810
9.80
【解析】
(1)[1].A.组装单摆须选用密度较大且直径较小的摆球,选项A错误;
B.组装单摆须选用轻且不易伸长的细线,选项B正确;
C.实验时须使摆球在同一竖直面内摆动,选项C正确;
D.单摆的摆角不得超过5°,否则单摆的运动就不是简谐运动,选项D错误;
故选BC。
(2)[2].小球直径为d=0.8cm+0.05mm×2=0.810cm;
(3)[3].单摆的周期为
由
可得
由图像可知
解得
g=9.80m/s2
同课章节目录
- 第一章 机械振动
- 第01节 初识简谐运动
- 第02节 简谐运动的力和能量特征
- 第03节 简谐运动的公式描述
- 第04节 探究单摆的振动周期
- 第05节 用单摆测定重力加速度
- 第06节 受迫振动 共振
- 第二章 机械波
- 第01节 机械波的产生和传播
- 第02节 机械波的图象描述
- 第03节 惠更斯原理及其应用
- 第04节 波的干涉与衍射
- 第05节 多普勒效应
- 第三章 电磁振荡与电磁波
- 第01节 电磁振荡
- 第02节 电磁场与电磁波
- 第03节 电磁波的发射、传播和接收
- 第04节 电磁波谱
- 第05节 电磁波的应用
- 第四章 光
- 第01节 光的折射定律
- 第02节 测定介质的折射率
- 第03节 认识光的全反射现象
- 第04节 光的干涉
- 第05节 用双缝干涉实验测定光的波长
- 第06节 光的衍射和偏振
- 第07节 激光
- 第五章 相对论
- 第01节 狭义相对论的基本原理
- 第02节 时空相对性
- 第03节 质能方程与相对论速度合成
- 第04节 广义相对论
- 第05节 宇宙学简介
