苏科版数学八年级下册 8.2可能性的大小 教案
文档属性
| 名称 | 苏科版数学八年级下册 8.2可能性的大小 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 98.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-11 16:12:54 | ||
图片预览

文档简介
数学教学设计
教 材:义务教育教科书·数学(八年级下册)
8.2 可能性的大小
教学目标 知识技能目标:活动中体验随机事件发生的可能性有大有小;
过程方法目标:让学生感受数学学习中,从猜想→试验并收集、整理、描述数据→分析试验结果,感受影响可能性大小的因素;
情感态度价值观目标:感受数学就在自己身边,体会数学学习与现实的联系。进一步培养学生求实态度和科学精神.
教学重点 体会随机事件发生的可能性是有大有小的.
教学难点 理解随机事件发生的可能性有大有小.
教学过程(教师) 学生活动 设计意图
情境引入:找朋友 让一名学生蒙起双眼,其他同学站在他的周围,并在游戏开始前让他猜一猜:他一定能找到他的同桌吗?一定能找到同一小组的同学吗?如果不能确定,那么这两种可能性哪一个更大一些?
游戏规则:先请3名同学来做游戏,其中2名同学是同桌关系,其中一名同学蒙上双眼,另2位同学站在周围转圈,当中间这位蒙上双眼的学生喊停时,他手指指向哪位同学,就算找到这位同学.在玩之前同学们请猜一猜,蒙上双眼的学生从2位同学中一定能找到他的同桌吗?再请2名同学来,从5名同学中找同桌,蒙上双眼的学生一定能找到他的同桌吗?两个事件中找到他的同桌的可能性相同吗?
参与游戏,积极思考,在活动中体验随机事件发生的可能性有大有小.
把学生学习的内容和实际情景联系起来,让学生在现实情境中解决问题.用“找朋友”这样的情景引入,让学生亲身经历将实际问题抽象成数学模型,并进行解释与应用,与教学内容紧密相关.
活动一:摸球实验 (1) 在一个不透明的袋子中装有3个白球和4个黄球,每个球除颜色外都相同.
①你认为从中任意摸出1个球,摸到的球可能是哪种颜色?②你认为摸到哪种颜色球的可能性大?③每位同学从袋子中摸1个球,记下所摸球的颜色,然后将球放回并摇匀;④按③的方法请几位同学轮流摸球,并将试验结果填入下表:
试验结果
频数划记
频数
频率
摸到白球
摸到黄球
我们用实验验证了大家的猜想.
(2)怎样才能让摸到白球的可能性比黄球大呢?(3)怎样才能让摸到白球的可能性更大呢?(4)摸到白球的可能性与哪些因素有关呢?
动手实践,小组活动,在实验中交流.
在摸球试验中,每次摸到的球的颜色是随机的,摸到每个球的可能性是一样的,摸到白球的可能性与白球的数量以及总的球数有关.
通过设计巧妙合理的问题,为学生创造更广阔的思维空间.学生在自主活动中不断的探究问题、发现问题、总结问题,培养学生分析解决问题的能力.
通过学生活动,给足学生空间和时间,让学生在“做中学”,经历知识的形成过程,让学生对知识的认识由感性上升到理性.
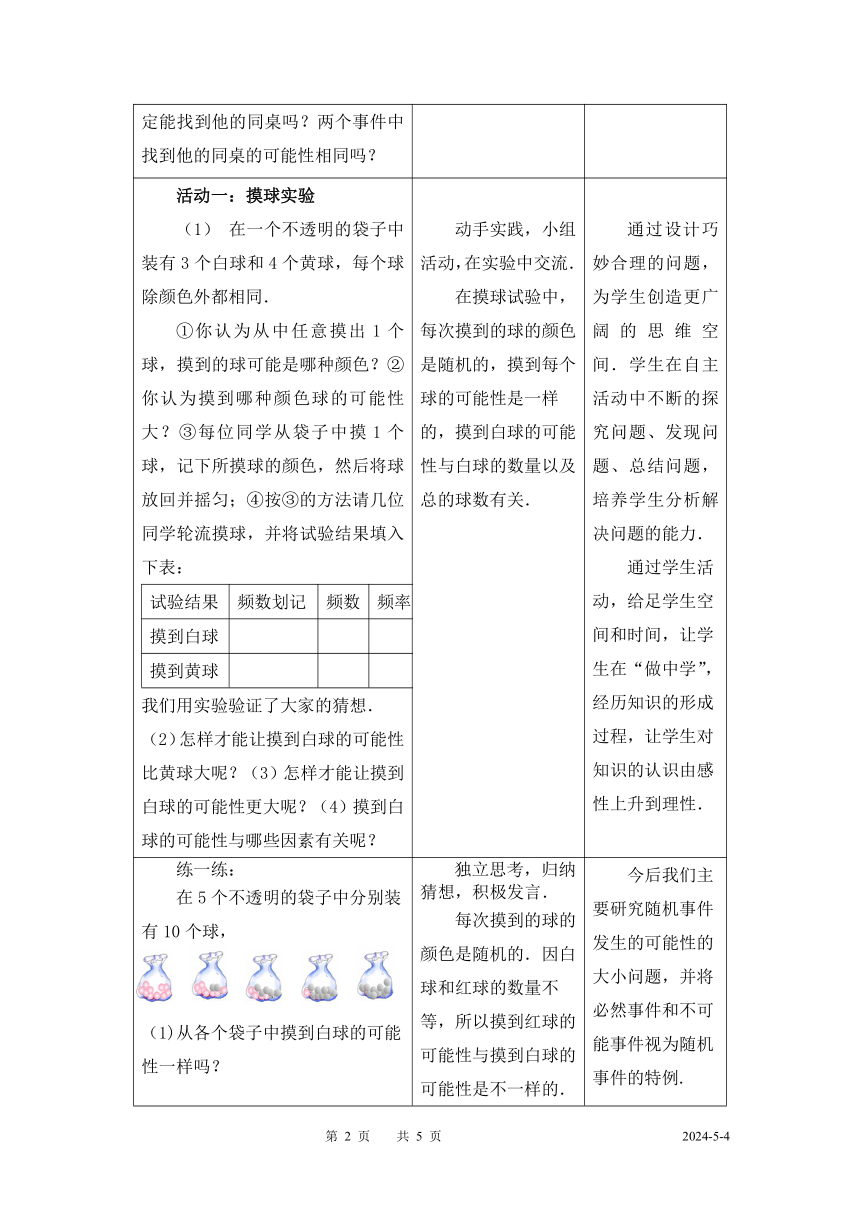
练一练: 在5个不透明的袋子中分别装有10个球,
从各个袋子中摸到白球的可能性一样吗?
请将袋子的序号按摸到白球的可能性从小到大的顺序排列. 独立思考,归纳猜想,积极发言.
每次摸到的球的颜色是随机的.因白球和红球的数量不等,所以摸到红球的可能性与摸到白球的可能性是不一样的.
从摸球的实验中体会到随机事件发生的可能性有大有小. 今后我们主要研究随机事件发生的可能性的大小问题,并将必然事件和不可能事件视为随机事件的特例.
活动二:掷骰子 任意地抛掷一枚均匀的骰子,当骰子落地时,
(1)朝上的点数有哪些可能?
(2)任意地抛掷一枚均匀的骰子,先后抛掷2次.
我们一起来实验.
试验结果
频数
频率
2次点数相同
2次点数不同
两个点数之和
频数
频率
2
3
4
5
6
7
8
9
10
11
12
(3)如果全班同学每人抛掷2枚均匀的骰子,记下朝上的点数的数字,并计算出2次点数之和.(请思考:2次点数之和会有哪些可能的结果呢?抛掷若干次之后,点数之和是几出现的可能性比较大呢?)
在这些结果中,它们发生的可能性一样吗?你认为哪些结果发生的可能性大?
小结:抛掷骰子结果可能性有大有小,事件可能性的大小可以通过实验来估计.
动手实践,合作学习,小组认真活动后得到结果:
每组的记录员将结果填入黑板上的表格中.班长完成全班的数据和.
在试验过程中,教师要关注整个试验过程,确保试验的随机性.汇总填表后,要引导学生对试验的数据发表意见,感悟到频率体现了随机事件发生的可能性的大小,从而认识到随机事件的可能性的大小.
重视渗透统计与概率之间的联系,通过频率来估计随机事件发生可能性的大小,通过样本的有关数据对总体的可能性作出估计,符合学生的年龄特点和心理发展规律,让学生乐于接触的,进一步发展学生的随机观念.
活动三:转转盘 1.如图,转盘被分成4个相等的扇形.转动转盘,当指针停在哪个数据区域上,就说它指向几.当指针停在边界时,重新转动转盘,直到指向一个数据.
2.不一样的转盘,转盘被分成8个相等的扇形.
转动转盘一次,指针落在哪个颜色区域上的可能性最大?落在哪个颜色区域上的可能性最小?
全班同学轮流转动转盘一次,当转盘停止时,记录指针落在区域的颜色?
(3)你做出的猜想与实验结果一致吗?
小结:随机事件的可能性大小与面积有关.
全民参与游戏,积极思考,生生评价:
全班同学轮流转动转盘一次,当转盘停止时,记录指针落在区域的颜色.
总结:在这个试验中,任意旋转转盘1次,当转盘停止时,指针落在哪种颜色区域上是不确定的.由于各颜色区域的面积不等,所以指针落在不同颜色区域上的可能性也不一样.
转盘问题,有利于让学生初步感受到几何概型.设计了三个问题,由简单到复杂,由浅入深,体现了活动开展的层次性.在合作学习的过程中,随着学生之间不同程度的交往和互相配合、互相帮助,增强他们的集体荣誉感、责任感,以及交际能力、合作能力.
拓展延伸,小组交流 刚才的活动对你有没有启发?下面就请大家放飞思维的翅膀,请每人分别举出一些随机事件,在小组内交流,说一说举得事件中,谁发生的可能性大,谁发生的可能性小?生活中有很多类似这样的问题.想一想:请问下列事件哪些可能性大?哪些可能性小?
1.在一副扑克牌中任意抽出一张牌,这张牌是大王的可能性大还是红桃的可能性大?
2.在你们班级任意找二名学生,他们是同一年出生的和同一个月出生的哪一种可能性较大?
3.买一张彩票,中奖的可能性大还是不中奖的可能性大?
小组交流讨论(请小组派代表在全班交流).
小结:随机事件发生的可能性有大有小,事件可能性的大小也可以通过分析来估计.
再次把学生引回到具体的实际问题,并组织学生小组讨论、合作交流,引导学生对身边随机事件作数学思考,让不同的认识进行碰撞,每个学生在进行数学表达的同时,可以不断获取新的信息,建构并完善自我认知结构.
学海拾贝,畅所欲言 1.我们的收获:学习了本节课,你有哪些收获?
2.小结:这节课我们做了很多活动,举例说明随机事件发生的可能性是有大有小的?
同学们畅所欲言,说出自己的想法,积极反思一节课的收获,充满成就感.
例如:今天的哪一个活动你最感兴趣?从中你得到什么启发?你从其他同学的表现中学到了什么? 把总结评价的主动权充分地交给学生,同时给学生一个开放的思维空间,培养学生的知识整理与语言表达能力,情绪会被再度调动起来,从而起到认知升华的作用.
第 1 页 共 5 页 2017-2-20
教 材:义务教育教科书·数学(八年级下册)
8.2 可能性的大小
教学目标 知识技能目标:活动中体验随机事件发生的可能性有大有小;
过程方法目标:让学生感受数学学习中,从猜想→试验并收集、整理、描述数据→分析试验结果,感受影响可能性大小的因素;
情感态度价值观目标:感受数学就在自己身边,体会数学学习与现实的联系。进一步培养学生求实态度和科学精神.
教学重点 体会随机事件发生的可能性是有大有小的.
教学难点 理解随机事件发生的可能性有大有小.
教学过程(教师) 学生活动 设计意图
情境引入:找朋友 让一名学生蒙起双眼,其他同学站在他的周围,并在游戏开始前让他猜一猜:他一定能找到他的同桌吗?一定能找到同一小组的同学吗?如果不能确定,那么这两种可能性哪一个更大一些?
游戏规则:先请3名同学来做游戏,其中2名同学是同桌关系,其中一名同学蒙上双眼,另2位同学站在周围转圈,当中间这位蒙上双眼的学生喊停时,他手指指向哪位同学,就算找到这位同学.在玩之前同学们请猜一猜,蒙上双眼的学生从2位同学中一定能找到他的同桌吗?再请2名同学来,从5名同学中找同桌,蒙上双眼的学生一定能找到他的同桌吗?两个事件中找到他的同桌的可能性相同吗?
参与游戏,积极思考,在活动中体验随机事件发生的可能性有大有小.
把学生学习的内容和实际情景联系起来,让学生在现实情境中解决问题.用“找朋友”这样的情景引入,让学生亲身经历将实际问题抽象成数学模型,并进行解释与应用,与教学内容紧密相关.
活动一:摸球实验 (1) 在一个不透明的袋子中装有3个白球和4个黄球,每个球除颜色外都相同.
①你认为从中任意摸出1个球,摸到的球可能是哪种颜色?②你认为摸到哪种颜色球的可能性大?③每位同学从袋子中摸1个球,记下所摸球的颜色,然后将球放回并摇匀;④按③的方法请几位同学轮流摸球,并将试验结果填入下表:
试验结果
频数划记
频数
频率
摸到白球
摸到黄球
我们用实验验证了大家的猜想.
(2)怎样才能让摸到白球的可能性比黄球大呢?(3)怎样才能让摸到白球的可能性更大呢?(4)摸到白球的可能性与哪些因素有关呢?
动手实践,小组活动,在实验中交流.
在摸球试验中,每次摸到的球的颜色是随机的,摸到每个球的可能性是一样的,摸到白球的可能性与白球的数量以及总的球数有关.
通过设计巧妙合理的问题,为学生创造更广阔的思维空间.学生在自主活动中不断的探究问题、发现问题、总结问题,培养学生分析解决问题的能力.
通过学生活动,给足学生空间和时间,让学生在“做中学”,经历知识的形成过程,让学生对知识的认识由感性上升到理性.
练一练: 在5个不透明的袋子中分别装有10个球,
从各个袋子中摸到白球的可能性一样吗?
请将袋子的序号按摸到白球的可能性从小到大的顺序排列. 独立思考,归纳猜想,积极发言.
每次摸到的球的颜色是随机的.因白球和红球的数量不等,所以摸到红球的可能性与摸到白球的可能性是不一样的.
从摸球的实验中体会到随机事件发生的可能性有大有小. 今后我们主要研究随机事件发生的可能性的大小问题,并将必然事件和不可能事件视为随机事件的特例.
活动二:掷骰子 任意地抛掷一枚均匀的骰子,当骰子落地时,
(1)朝上的点数有哪些可能?
(2)任意地抛掷一枚均匀的骰子,先后抛掷2次.
我们一起来实验.
试验结果
频数
频率
2次点数相同
2次点数不同
两个点数之和
频数
频率
2
3
4
5
6
7
8
9
10
11
12
(3)如果全班同学每人抛掷2枚均匀的骰子,记下朝上的点数的数字,并计算出2次点数之和.(请思考:2次点数之和会有哪些可能的结果呢?抛掷若干次之后,点数之和是几出现的可能性比较大呢?)
在这些结果中,它们发生的可能性一样吗?你认为哪些结果发生的可能性大?
小结:抛掷骰子结果可能性有大有小,事件可能性的大小可以通过实验来估计.
动手实践,合作学习,小组认真活动后得到结果:
每组的记录员将结果填入黑板上的表格中.班长完成全班的数据和.
在试验过程中,教师要关注整个试验过程,确保试验的随机性.汇总填表后,要引导学生对试验的数据发表意见,感悟到频率体现了随机事件发生的可能性的大小,从而认识到随机事件的可能性的大小.
重视渗透统计与概率之间的联系,通过频率来估计随机事件发生可能性的大小,通过样本的有关数据对总体的可能性作出估计,符合学生的年龄特点和心理发展规律,让学生乐于接触的,进一步发展学生的随机观念.
活动三:转转盘 1.如图,转盘被分成4个相等的扇形.转动转盘,当指针停在哪个数据区域上,就说它指向几.当指针停在边界时,重新转动转盘,直到指向一个数据.
2.不一样的转盘,转盘被分成8个相等的扇形.
转动转盘一次,指针落在哪个颜色区域上的可能性最大?落在哪个颜色区域上的可能性最小?
全班同学轮流转动转盘一次,当转盘停止时,记录指针落在区域的颜色?
(3)你做出的猜想与实验结果一致吗?
小结:随机事件的可能性大小与面积有关.
全民参与游戏,积极思考,生生评价:
全班同学轮流转动转盘一次,当转盘停止时,记录指针落在区域的颜色.
总结:在这个试验中,任意旋转转盘1次,当转盘停止时,指针落在哪种颜色区域上是不确定的.由于各颜色区域的面积不等,所以指针落在不同颜色区域上的可能性也不一样.
转盘问题,有利于让学生初步感受到几何概型.设计了三个问题,由简单到复杂,由浅入深,体现了活动开展的层次性.在合作学习的过程中,随着学生之间不同程度的交往和互相配合、互相帮助,增强他们的集体荣誉感、责任感,以及交际能力、合作能力.
拓展延伸,小组交流 刚才的活动对你有没有启发?下面就请大家放飞思维的翅膀,请每人分别举出一些随机事件,在小组内交流,说一说举得事件中,谁发生的可能性大,谁发生的可能性小?生活中有很多类似这样的问题.想一想:请问下列事件哪些可能性大?哪些可能性小?
1.在一副扑克牌中任意抽出一张牌,这张牌是大王的可能性大还是红桃的可能性大?
2.在你们班级任意找二名学生,他们是同一年出生的和同一个月出生的哪一种可能性较大?
3.买一张彩票,中奖的可能性大还是不中奖的可能性大?
小组交流讨论(请小组派代表在全班交流).
小结:随机事件发生的可能性有大有小,事件可能性的大小也可以通过分析来估计.
再次把学生引回到具体的实际问题,并组织学生小组讨论、合作交流,引导学生对身边随机事件作数学思考,让不同的认识进行碰撞,每个学生在进行数学表达的同时,可以不断获取新的信息,建构并完善自我认知结构.
学海拾贝,畅所欲言 1.我们的收获:学习了本节课,你有哪些收获?
2.小结:这节课我们做了很多活动,举例说明随机事件发生的可能性是有大有小的?
同学们畅所欲言,说出自己的想法,积极反思一节课的收获,充满成就感.
例如:今天的哪一个活动你最感兴趣?从中你得到什么启发?你从其他同学的表现中学到了什么? 把总结评价的主动权充分地交给学生,同时给学生一个开放的思维空间,培养学生的知识整理与语言表达能力,情绪会被再度调动起来,从而起到认知升华的作用.
第 1 页 共 5 页 2017-2-20
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
