苏科版数学八年级下册 9.3平行四边形 复习 教案
文档属性
| 名称 | 苏科版数学八年级下册 9.3平行四边形 复习 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 71.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-11 16:31:12 | ||
图片预览

文档简介
平行四边形 复习课
教学目标:
1、回顾平行四边形、矩形、菱形、正方形的概念,帮助学生梳理它们之间的关系,掌握其性质定理与判定定理;
2、进一步培养学生观察、操作的能力;丰富学生对图形的认识和感受,并能进行相关的计算和证明;
重点和难点:
对本章所涉及到的性质和判定能进行灵活运用;
教学过程:
一、拼一拼 说一说
用两个全等的含有30°角的三角板来拼四边形,能拼出多少个不同的四边形?请你动手画一画.
二、小试牛刀
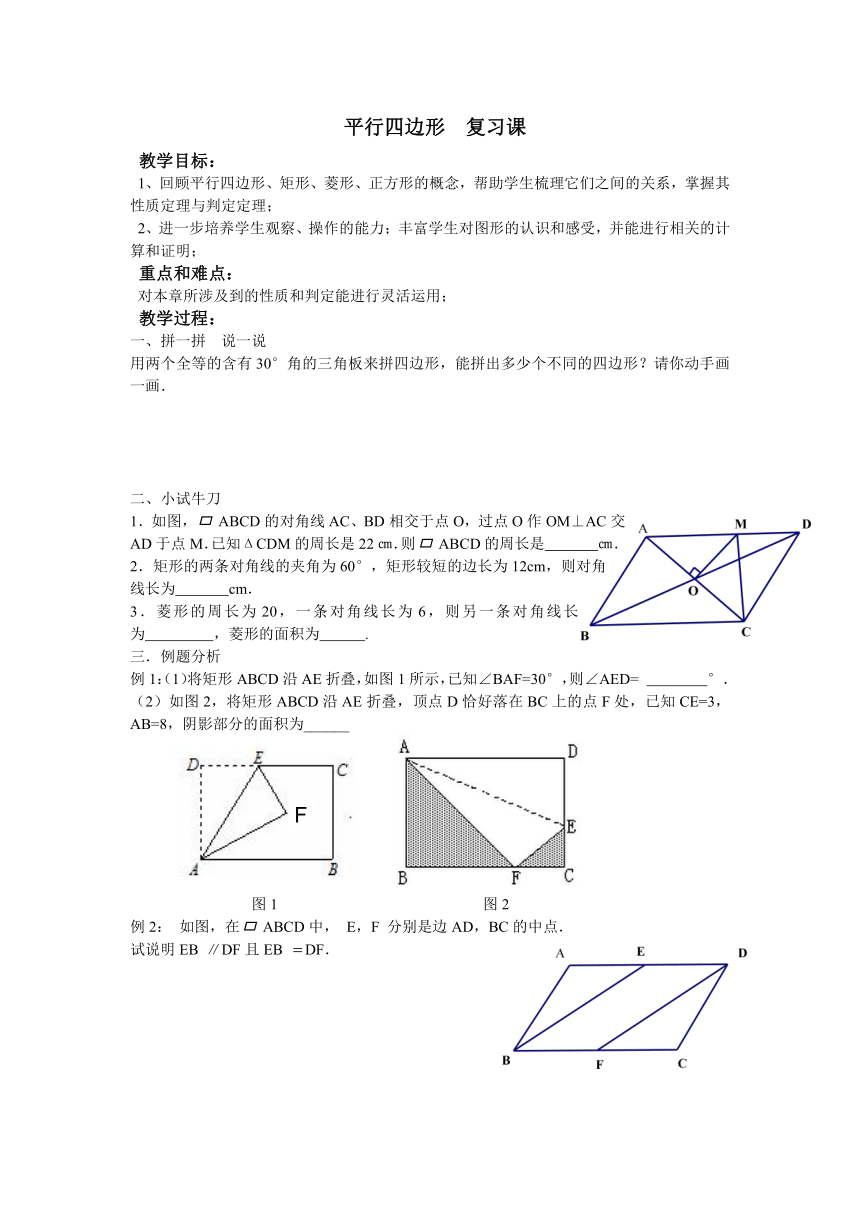
1.如图,ABCD的对角线AC、BD相交于点O,过点O作OM⊥AC交AD于点M.已知ΔCDM的周长是22㎝.则ABCD的周长是 ㎝.
2.矩形的两条对角线的夹角为60°,矩形较短的边长为12cm,则对角线长为 cm.
3.菱形的周长为20,一条对角线长为6,则另一条对角线长为 ,菱形的面积为 .
三.例题分析
例1:(1)将矩形ABCD沿AE折叠,如图1所示,已知∠BAF=30°,则∠AED= °.
(2)如图2,将矩形ABCD沿AE折叠,顶点D恰好落在BC上的点F处,已知CE=3,AB=8,阴影部分的面积为______
图1 图2
例2: 如图,在ABCD中, E,F 分别是边AD,BC的中点.
试说明EB ∥DF且EB DF.
变式1
已知:如图,在ABCD中, E,F 分别是边AD,BC的中点,若AF交BE于G,CE交DF于H,由上题的结论,你能不能迅速判断四边形EGFH是什么特殊的四边形?请简单说明理由。
变式1-1
已知:如图,在ABCD中, E,F 分别是边AD,BC的中点,若AF交BE于G,CE交DF于H,若AB⊥BC,试判断四边形EGFH的形状,并说明理由.
变式1-2
已知:如图,在ABCD中, E,F 分别是边AD,BC的中点,若AF交BE于G,CE交DF于H,若BC=2AB,试判断四边形EGFH的形状,并说明理由.
三、小结与回顾
四、拓展提高
如图,正方形ABCD,AC、BD相交于点O,点E在AC上,连接BE,作AG⊥BE,垂足为G,且交直线BD于F。
(1)试说明:OE=OF;
(2)若点E在AC的延长线上,其余条件不变,(1)的结论还成立吗?画出图形,并说明理由。
教学目标:
1、回顾平行四边形、矩形、菱形、正方形的概念,帮助学生梳理它们之间的关系,掌握其性质定理与判定定理;
2、进一步培养学生观察、操作的能力;丰富学生对图形的认识和感受,并能进行相关的计算和证明;
重点和难点:
对本章所涉及到的性质和判定能进行灵活运用;
教学过程:
一、拼一拼 说一说
用两个全等的含有30°角的三角板来拼四边形,能拼出多少个不同的四边形?请你动手画一画.
二、小试牛刀
1.如图,ABCD的对角线AC、BD相交于点O,过点O作OM⊥AC交AD于点M.已知ΔCDM的周长是22㎝.则ABCD的周长是 ㎝.
2.矩形的两条对角线的夹角为60°,矩形较短的边长为12cm,则对角线长为 cm.
3.菱形的周长为20,一条对角线长为6,则另一条对角线长为 ,菱形的面积为 .
三.例题分析
例1:(1)将矩形ABCD沿AE折叠,如图1所示,已知∠BAF=30°,则∠AED= °.
(2)如图2,将矩形ABCD沿AE折叠,顶点D恰好落在BC上的点F处,已知CE=3,AB=8,阴影部分的面积为______
图1 图2
例2: 如图,在ABCD中, E,F 分别是边AD,BC的中点.
试说明EB ∥DF且EB DF.
变式1
已知:如图,在ABCD中, E,F 分别是边AD,BC的中点,若AF交BE于G,CE交DF于H,由上题的结论,你能不能迅速判断四边形EGFH是什么特殊的四边形?请简单说明理由。
变式1-1
已知:如图,在ABCD中, E,F 分别是边AD,BC的中点,若AF交BE于G,CE交DF于H,若AB⊥BC,试判断四边形EGFH的形状,并说明理由.
变式1-2
已知:如图,在ABCD中, E,F 分别是边AD,BC的中点,若AF交BE于G,CE交DF于H,若BC=2AB,试判断四边形EGFH的形状,并说明理由.
三、小结与回顾
四、拓展提高
如图,正方形ABCD,AC、BD相交于点O,点E在AC上,连接BE,作AG⊥BE,垂足为G,且交直线BD于F。
(1)试说明:OE=OF;
(2)若点E在AC的延长线上,其余条件不变,(1)的结论还成立吗?画出图形,并说明理由。
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
