3.3.3 简单的线性规划问题(2) 课件(23张PPT)
文档属性
| 名称 | 3.3.3 简单的线性规划问题(2) 课件(23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 916.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-10 18:23:32 | ||
图片预览








文档简介
一、问题情景
某校办工厂有方木料90m3,五合板600m2,正准备为外校新生加工新桌椅和书橱出售.已知生产每张书桌需要方木料0.1m3,五合板2m2,生产每个书橱需要方木料0.2m3,五合板1m2,出售一张书桌可获利润80元,出售一张书橱可获利润120元.
(1)假设你是工厂的生产科长,请你按要求设计出工厂的生产方案。
方案一:若只生产书桌,用完五合板,可生产书桌300张,可获得利润80×300=24000元,但方木料没有用完.
方案二:若只生产书橱,用完方木料,可生产450张书橱,可获得利润120×450=54000元,但五合板没有用完.
(2)设生产书桌x张,书橱y张,利润z元,写出x,y应满足的条件以及Z与x,y之间的函数关系式.
约束条件为 :
目标函数为:
(3)如果你是厂长,为使工厂原料充分利用,问怎么安排能够使资源最大限度的利用,且可获得最大利润?
方案三、生产书桌100张,书橱400张,有最大利润为56000元.
在上面两种情况下,原料都没有充分利用,造成了资源浪费,那么该怎么安排能够使资源最大限度的利用,且可获得最大利润?
二、线性规划在实际中的应用
线性规划的理论和方法主要在两类问题中得到应用,
一是在人力、物力、资金等资源一定的条件下,如何使用它们来完
成最多的任务;
二是给定一项任务,如何合理安排和规划,能以最少的人力、
物力、资金等资源来完成该项任务.
下面我们就来看看线性规划在实际中的一些应用:
例题
例1 某工厂用A,B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算,该厂所有可能的日生产安排是什么?若生产一件甲产品可获利润2万元,生产一件乙产品可获利润3万元,则如何安排日生产,可使工厂所获利润最大?
分析:将已知数据列成表格
产品
A
B
耗时
甲
4
1h
乙
4
2h
16
12
8h
解 设甲、乙两种产品的产量分别为x,y件,工厂利润z万元
约束条件为:
目标函数是:
作出二元一次不等式组所表示的平面区域,即可行域.
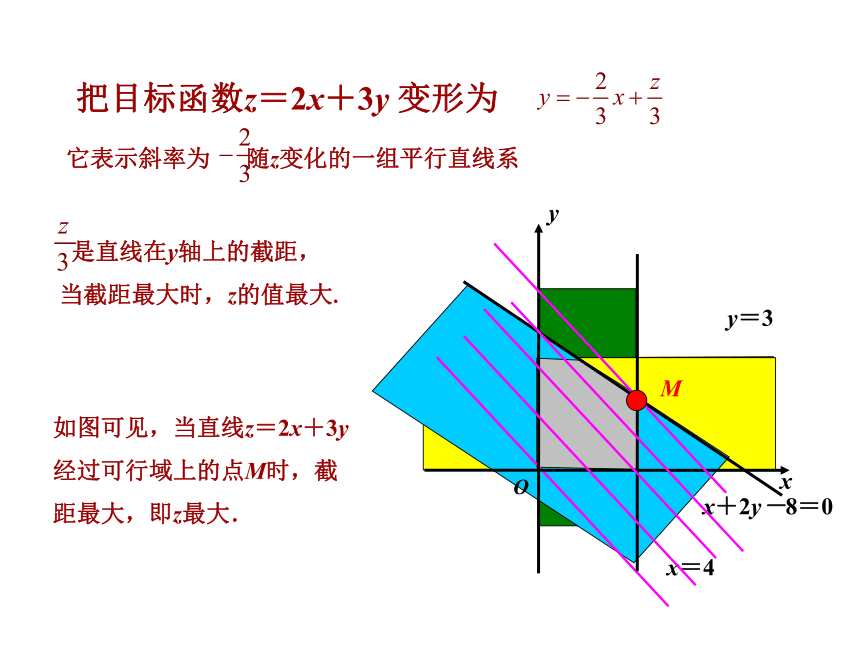
把目标函数z=2x+3y 变形为
y
x
O
x+2y-8=0
y=3
x=4
它表示斜率为 随z变化的一组平行直线系
是直线在y轴上的截距,当截距最大时,z的值最大.
如图可见,当直线z=2x+3y 经过可行域上的点M时,截距最大,即z最大.
M
M点是两条直线的交点,解方程组
得M点的坐标为:
所以zmax=2 x+3y=14
由此可知,每天生产甲产品4件、乙产品2件时,工厂可得最大最大利润14万元.
例2 投资生产A产品时,每生产一百吨需要资金200万元,需场地200m2,可获利润300万元;投资生产B产品时,每生产一百米需要资金300万元,需场地100m2,可获利润200万元.现某单位可使用资金1400万元,场地900m2,问:应作怎样的组合投资,可获利最大?
资金(百万元)
场地(百平方米)
利润(百万元)
A产品(百吨)
2
2
3
B产品(百米)
3
1
2
限制
14
9
分析 将已知数据列成表格
解 设生产A产品x百吨,生产B产品y百米,利润为S百万元,则约束条件为
目标函数为
作出可行域
把目标函数S=3x+2y 变形为
A
y
2x+y=9
x
O
2x+3y=14
它表示斜率为
随S变化的一组平行直线系
是直线在y轴上的截距,当截距最大时,S的值最大.
如图可见,当直线S=3x+2y 经过可行域上的点A时,截距最大,即S最大.
A点是两条直线的交点,解方程组
得A点的坐标为:
所以Smin=3x+2y=14.75
由此可知,,生产A产品325t,生产B产品250m时,获利最大,且最大利润为1475万元.
例3 营养学家指出,成人良好的日常饮食应该至少提供0.075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪,1kg食物A含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费28元;而1食物B含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费21元。为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少kg?
食物/kg
碳水化合物kg
蛋白质kg
脂肪kg
花费(元)
A
0.105
0.07
0.14
28
B
0.105
0.14
0.07
21
成人日常需要
0.075
0.06
0.06
分析:将已知数据列成表格
解 设每天食用xkg食物A,ykg食物B,总成本为z,则线性约束条件为:
目标函数为:z=28x+21y
作出二元一次不等式组所表示的平面区域,即可行域
把目标函数z=28x+21y 变形为
x
y
o
5/7
5/7
6/7
3/7
3/7
6/7
它表示斜率为
随z变化的一组平行直线系
是直线在y轴上的截 距,当截距最小时,z的值最小.
M
如图可见,当直线z=28x+21y 经过可行域上的点M时,截距最小,即z最小.
M点是两条直线的交点,解方程组
得M点的坐标为:
所以zmin=28x+21y=16
由此可知,每天食用食物A143g,食物B约571g,能够满足日常饮食要求,又使花费最低,最低成本为16元.
三、练习题
1. 某厂拟生产甲、乙两种适销产品,每件销售收入分别为3000元、2000元,甲、乙产品都需要在A,B两种设备上加工,在每台A,B上加工1件甲所需工时分别为1h、2h,加工一件乙所需工时分别为2h、1h,A,B两种设备每月有效使用台数分别为400h/台和500h/台.如何安排生产可使收入最大?
设每月生产甲产品x件,生产乙产品y件,每月收入为z,目标函数为Z=3x+2y,满足的条件是
Z= 3x+2y 变形为
它表示斜率为 的直线系,Z与这条直线的截距有关.
x
y
O
400
200
250
500
当直线经过点M时,截距最大,Z最大.
M
解方程组
可得M(200,100)
Zmax =3x+2y=800
故生产甲产品200件,乙产品100件,收入最大,为80万元.
2.某人准备投资1200万元兴办一所完全中学.对教育市场进行调查后,他得到了下面的数据表格(以班级为单位)
分别用数学关系式和图形表示上述限制条件.若根据有关部门的规定,初中每人每年可收学费1600元,高中每人每年可收学费2700元.因生源和环境等条件限制,办学规模以20至30个班为宜(含20个与30个)那么开设初中班和高中班多少个?每年收费的学费总额最多?
学段
班级学生数
配备教师数
硬件建设(万元)
教师年薪(万元)
初中
45
2
26/班
2/人
高中
40
3
54/班
2/人
把上面四个不等式合在一起,得到
y
x
20
30
40
20
30
o
另外,开设的班级不能为负,则x≥0,y≥0.
而由于资金限制,26x+54y+2×2x+2×3y≤1200
解 设开设初中班x个,高中班y个。因办学规模以20~30个班为宜,所以, 20≤x+y≤30
y
x
20
30
40
20
30
o
由图可以看出,当直线Z=7.2x+10.8y经过可行域上的点M时,截距最大,即Z最大.
设收取的学费总额为Z万元,则目标函数
Z=0.16×45x+0.27×40y=7.2x+10.8y.
Z=7.2x+10.8y变形为
它表示斜率为 的直线系,Z与这条直线的截距有关.
M
易求得M(20,10),则Zmax= 7.2x+10.8y =252
故开设20个初中班和10个高中班,
收取的学费最多,为252万元.
四、要点归纳与方法小结
(一)线性规划的两类重要实际问题的解题思路:
1.应准确建立数学模型,即根据题意找出约束条件,确定线性目标函数.
2.用图解法求得数学模型的解,即画出可行域,在可行域内求得使目标函数取得最值的解.(一般最优解在直线或直线的交点上,要注意斜率的比较.)
3.要根据实际意义将数学模型的解转化为实际问题的解,即结合实际情况求得最优解.
(二)线性规划问题的求解步骤:
(1)审:审题(将题目中数据列表),将实际问题转化为数学问题;
(2)设:设出变量,确定约束条件,建立目标函数;
(3)画:画出线性约束条件所表示的可行域,作出目标函数线;
(4)移:在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线;
(5)求:通过解方程组求出最优解;
(6)答:回答实际问题.
(三)对于有实际背景的线性规划问题,可行域通常是一个凸多边形区域,
此时变动直线的最佳位置一般通过这个凸多边形的顶点,因此,确定
其最优解,往往只需考虑在各个顶点的情形,通过比较,即可得最优解.
(四)本节课学习的数学思想:化归思想、数形结合思想.
某校办工厂有方木料90m3,五合板600m2,正准备为外校新生加工新桌椅和书橱出售.已知生产每张书桌需要方木料0.1m3,五合板2m2,生产每个书橱需要方木料0.2m3,五合板1m2,出售一张书桌可获利润80元,出售一张书橱可获利润120元.
(1)假设你是工厂的生产科长,请你按要求设计出工厂的生产方案。
方案一:若只生产书桌,用完五合板,可生产书桌300张,可获得利润80×300=24000元,但方木料没有用完.
方案二:若只生产书橱,用完方木料,可生产450张书橱,可获得利润120×450=54000元,但五合板没有用完.
(2)设生产书桌x张,书橱y张,利润z元,写出x,y应满足的条件以及Z与x,y之间的函数关系式.
约束条件为 :
目标函数为:
(3)如果你是厂长,为使工厂原料充分利用,问怎么安排能够使资源最大限度的利用,且可获得最大利润?
方案三、生产书桌100张,书橱400张,有最大利润为56000元.
在上面两种情况下,原料都没有充分利用,造成了资源浪费,那么该怎么安排能够使资源最大限度的利用,且可获得最大利润?
二、线性规划在实际中的应用
线性规划的理论和方法主要在两类问题中得到应用,
一是在人力、物力、资金等资源一定的条件下,如何使用它们来完
成最多的任务;
二是给定一项任务,如何合理安排和规划,能以最少的人力、
物力、资金等资源来完成该项任务.
下面我们就来看看线性规划在实际中的一些应用:
例题
例1 某工厂用A,B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算,该厂所有可能的日生产安排是什么?若生产一件甲产品可获利润2万元,生产一件乙产品可获利润3万元,则如何安排日生产,可使工厂所获利润最大?
分析:将已知数据列成表格
产品
A
B
耗时
甲
4
1h
乙
4
2h
16
12
8h
解 设甲、乙两种产品的产量分别为x,y件,工厂利润z万元
约束条件为:
目标函数是:
作出二元一次不等式组所表示的平面区域,即可行域.
把目标函数z=2x+3y 变形为
y
x
O
x+2y-8=0
y=3
x=4
它表示斜率为 随z变化的一组平行直线系
是直线在y轴上的截距,当截距最大时,z的值最大.
如图可见,当直线z=2x+3y 经过可行域上的点M时,截距最大,即z最大.
M
M点是两条直线的交点,解方程组
得M点的坐标为:
所以zmax=2 x+3y=14
由此可知,每天生产甲产品4件、乙产品2件时,工厂可得最大最大利润14万元.
例2 投资生产A产品时,每生产一百吨需要资金200万元,需场地200m2,可获利润300万元;投资生产B产品时,每生产一百米需要资金300万元,需场地100m2,可获利润200万元.现某单位可使用资金1400万元,场地900m2,问:应作怎样的组合投资,可获利最大?
资金(百万元)
场地(百平方米)
利润(百万元)
A产品(百吨)
2
2
3
B产品(百米)
3
1
2
限制
14
9
分析 将已知数据列成表格
解 设生产A产品x百吨,生产B产品y百米,利润为S百万元,则约束条件为
目标函数为
作出可行域
把目标函数S=3x+2y 变形为
A
y
2x+y=9
x
O
2x+3y=14
它表示斜率为
随S变化的一组平行直线系
是直线在y轴上的截距,当截距最大时,S的值最大.
如图可见,当直线S=3x+2y 经过可行域上的点A时,截距最大,即S最大.
A点是两条直线的交点,解方程组
得A点的坐标为:
所以Smin=3x+2y=14.75
由此可知,,生产A产品325t,生产B产品250m时,获利最大,且最大利润为1475万元.
例3 营养学家指出,成人良好的日常饮食应该至少提供0.075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪,1kg食物A含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费28元;而1食物B含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费21元。为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少kg?
食物/kg
碳水化合物kg
蛋白质kg
脂肪kg
花费(元)
A
0.105
0.07
0.14
28
B
0.105
0.14
0.07
21
成人日常需要
0.075
0.06
0.06
分析:将已知数据列成表格
解 设每天食用xkg食物A,ykg食物B,总成本为z,则线性约束条件为:
目标函数为:z=28x+21y
作出二元一次不等式组所表示的平面区域,即可行域
把目标函数z=28x+21y 变形为
x
y
o
5/7
5/7
6/7
3/7
3/7
6/7
它表示斜率为
随z变化的一组平行直线系
是直线在y轴上的截 距,当截距最小时,z的值最小.
M
如图可见,当直线z=28x+21y 经过可行域上的点M时,截距最小,即z最小.
M点是两条直线的交点,解方程组
得M点的坐标为:
所以zmin=28x+21y=16
由此可知,每天食用食物A143g,食物B约571g,能够满足日常饮食要求,又使花费最低,最低成本为16元.
三、练习题
1. 某厂拟生产甲、乙两种适销产品,每件销售收入分别为3000元、2000元,甲、乙产品都需要在A,B两种设备上加工,在每台A,B上加工1件甲所需工时分别为1h、2h,加工一件乙所需工时分别为2h、1h,A,B两种设备每月有效使用台数分别为400h/台和500h/台.如何安排生产可使收入最大?
设每月生产甲产品x件,生产乙产品y件,每月收入为z,目标函数为Z=3x+2y,满足的条件是
Z= 3x+2y 变形为
它表示斜率为 的直线系,Z与这条直线的截距有关.
x
y
O
400
200
250
500
当直线经过点M时,截距最大,Z最大.
M
解方程组
可得M(200,100)
Zmax =3x+2y=800
故生产甲产品200件,乙产品100件,收入最大,为80万元.
2.某人准备投资1200万元兴办一所完全中学.对教育市场进行调查后,他得到了下面的数据表格(以班级为单位)
分别用数学关系式和图形表示上述限制条件.若根据有关部门的规定,初中每人每年可收学费1600元,高中每人每年可收学费2700元.因生源和环境等条件限制,办学规模以20至30个班为宜(含20个与30个)那么开设初中班和高中班多少个?每年收费的学费总额最多?
学段
班级学生数
配备教师数
硬件建设(万元)
教师年薪(万元)
初中
45
2
26/班
2/人
高中
40
3
54/班
2/人
把上面四个不等式合在一起,得到
y
x
20
30
40
20
30
o
另外,开设的班级不能为负,则x≥0,y≥0.
而由于资金限制,26x+54y+2×2x+2×3y≤1200
解 设开设初中班x个,高中班y个。因办学规模以20~30个班为宜,所以, 20≤x+y≤30
y
x
20
30
40
20
30
o
由图可以看出,当直线Z=7.2x+10.8y经过可行域上的点M时,截距最大,即Z最大.
设收取的学费总额为Z万元,则目标函数
Z=0.16×45x+0.27×40y=7.2x+10.8y.
Z=7.2x+10.8y变形为
它表示斜率为 的直线系,Z与这条直线的截距有关.
M
易求得M(20,10),则Zmax= 7.2x+10.8y =252
故开设20个初中班和10个高中班,
收取的学费最多,为252万元.
四、要点归纳与方法小结
(一)线性规划的两类重要实际问题的解题思路:
1.应准确建立数学模型,即根据题意找出约束条件,确定线性目标函数.
2.用图解法求得数学模型的解,即画出可行域,在可行域内求得使目标函数取得最值的解.(一般最优解在直线或直线的交点上,要注意斜率的比较.)
3.要根据实际意义将数学模型的解转化为实际问题的解,即结合实际情况求得最优解.
(二)线性规划问题的求解步骤:
(1)审:审题(将题目中数据列表),将实际问题转化为数学问题;
(2)设:设出变量,确定约束条件,建立目标函数;
(3)画:画出线性约束条件所表示的可行域,作出目标函数线;
(4)移:在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线;
(5)求:通过解方程组求出最优解;
(6)答:回答实际问题.
(三)对于有实际背景的线性规划问题,可行域通常是一个凸多边形区域,
此时变动直线的最佳位置一般通过这个凸多边形的顶点,因此,确定
其最优解,往往只需考虑在各个顶点的情形,通过比较,即可得最优解.
(四)本节课学习的数学思想:化归思想、数形结合思想.
