3.1 平均数(1) 课件(17张PPT)
文档属性
| 名称 | 3.1 平均数(1) 课件(17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-11 09:58:19 | ||
图片预览





文档简介
3.1 平均数(1)
九年级(上册)
初中数学
3.1 平均数(1)
在篮球比赛中,队员的身高是反映球队实力的一个重要因素,如何衡量两个球队队员的身高?要比较两个球队队员的身高,需要收集哪些数据呢?
小明和小丽所在的A、B两个小组同学身高如下:
哪个小组同学的平均身高较高?你是如何判断的?
3.1 平均数(1)
A组(10人)/cm
B组(12人)/cm
159,164,160,152,154,169,170,
155,168,160
160,160,170,158,
170,168,158,170,
158,160,160,168
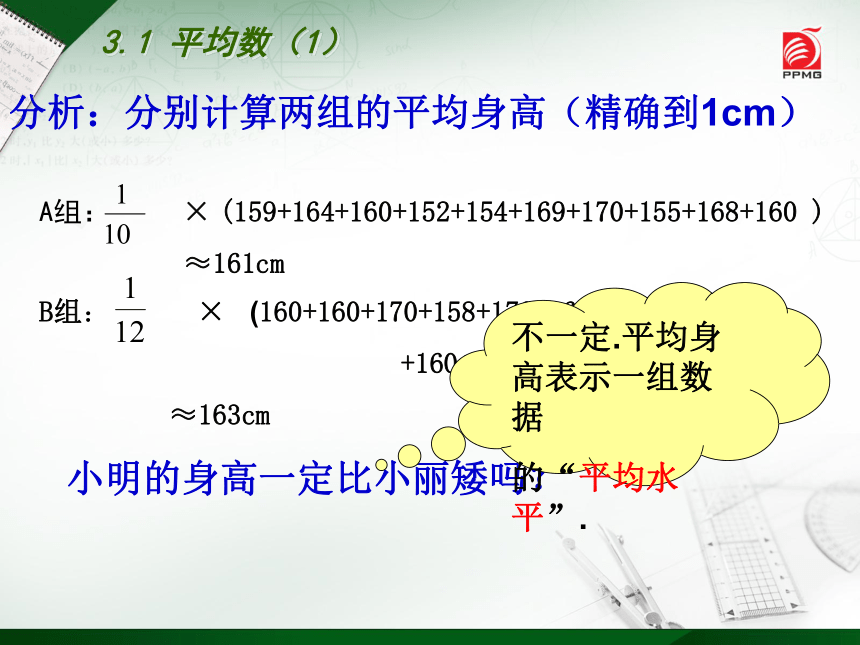
A组: × (159+164+160+152+154+169+170+155+168+160 )
≈161cm
B组: × (160+160+170+158+170+168+158+170+158
+160+160+168)
≈163cm
分析:分别计算两组的平均身高(精确到1cm)
3.1 平均数(1)
小明的身高一定比小丽矮吗?
不一定.平均身高表示一组数据
的“平均水平”.
通常,平均数可以用来表示一组数据的“平均水平”.
一般地,如果有n 个数
那么
叫做这 n 个数的算术平均数,简称平均数,
读作
“x 拔”.
3.1 平均数(1)
.
= × (159+164+160+152+154+169+170+155+168+160 )
≈161cm
= × (160+160+170+158+170+168+158+170+158
+160+160+168)
≈163cm
xA
xB
解:A组同学的平均身高:
B组同学的平均身高:
以上计算平均身高的计算过程还可以进一步简化吗?说一说你的想法.
3.1 平均数(1)
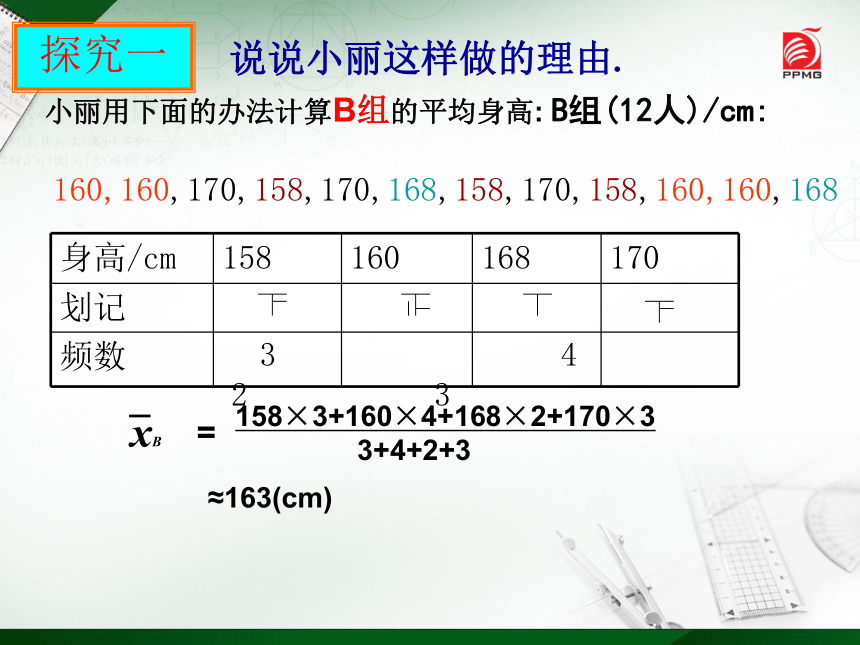
探究一
小丽用下面的办法计算B组的平均身高: B组(12人)/cm:
身高/cm
158
160
168
170
划记
频数
3 4 2 3
=
158×3+160×4+168×2+170×3
3+4+2+3
≈163(cm)
160,160,170,158,170,168,158,170,158,160,160,168
xB
说说小丽这样做的理由.
当一组数据中的若干个数据多次重复出现时可以考虑简便算法.
一般的:如果在n个数中,x1出现f1次,x2出现f2次, …,xk出现fk次,(这里f1+f2+…+fk=n),
那么x=
x1f1+x2f2+…+xkfk
n
平均数的计算方法2:
小明用下面的办法计算A组的平均身高
A组(10人)/cm:159,164,160,152,154,169,170,155,168,160
观察:这组数据都在 左右波动
160
①先将各个数据同时减去160,得到一组新数据:
-1、 4 、 0、 -8、 -6、9、 10、 -5、 8、 0
②再计算这组数据的平均数,得:
x’= (-1+4+0-8-6+9+10-5+8+0) =1.1
10
1
于是,平均身高x=x’+160=161.1≈161 (cm)
③
探究二
说说小明这样做的理由.
一般地,当一组数据 都接近同一个数据a时,可将各数据同时减去这个数a,得到一组新的数据
那么
因此
a
x
x
a
x
x
a
x
x
n
n
-
=
?
-
=
?
-
=
?
,
,
,
2
2
1
1
L
分步计算法
平均数的计算方法3:
某体操队20名队员的身高如下(单位:cm)
172,170,169,172,162,167,168,165,172,170,160,
175,168,165,171,169,167,174,170,164.
计算这些队员的平均身高.(精确到1cm)
解:①取一个常数170,以上数据同时减去170得到一
组新数据:2、0、-1、2、-8、-3、-2、-5、2、0、
-10、5、-2、-5、1、-1、-3、4、0、-6
x′=-1.5
x=170-1.5=168.5≈169(cm)
②计算这组新数据的平均数:
③原数据的平均数:
例题1
例题2
设有甲、乙、丙三种可混合包装的食品,它们的单价分别是1.8元,2.5元,3.2元,现取甲种食品50公斤,乙种食品40公斤,丙种食品10公斤,把这三种食品混合后每公斤的单价是多少?
1. 小明本周每天睡眠时间如下8,9,7,9,7,8,8,则本周小明的平均睡眠时间是 小时.
2. 一组数据85,80,x,90,它的平均数是85,求x值.
课堂练习
(85+80+x+90)
=85
x =85
8
×
方程思想
3. 11人出去采集标本,其中每人采6件的有2人,每人采3件的有4人,每人采4件的5人,求平均每人采集标本数.
×(6×2+3×4+ 4×5)
=4
已知:数据X1,X2, …,Xn的平均数为 X(以下填空用X的代数式表示)
⑴则X1+1, X2+1 … Xn+1的平均数为
⑵则X1-2, X2-2 … Xn-2的平均数为
⑶则3X1, 3X2 … 3Xn的平均数为
X+1
3X
X-2
拓展与延伸:
归纳:如果两组数据x1,x2,…,xn和y1,y2,…,yn的平均数分别是x和y,
则新数据ax1,ax2,…,axn的平均数是ax,
新数据x1+y1,x2+y2,…,xn+yn的平均数是x+y
算术平均数:在统计里,平均数是重要概念之一,它表示一组数据的”平均水平”.
公式:
(1)
(2)
(3)
注意:区别这三个公式的解题中的应用,以达到简化计算为目的地有选择地进行应用。
3.1 平均数(1)
体操比赛7位裁判给某选手的打分如下:
9.8,9.5,9.5 ,9.5,9.3,9.2,8.5.
计算这位选手的平均得分.
例题
3.1 平均数(1)
九年级(上册)
初中数学
3.1 平均数(1)
在篮球比赛中,队员的身高是反映球队实力的一个重要因素,如何衡量两个球队队员的身高?要比较两个球队队员的身高,需要收集哪些数据呢?
小明和小丽所在的A、B两个小组同学身高如下:
哪个小组同学的平均身高较高?你是如何判断的?
3.1 平均数(1)
A组(10人)/cm
B组(12人)/cm
159,164,160,152,154,169,170,
155,168,160
160,160,170,158,
170,168,158,170,
158,160,160,168
A组: × (159+164+160+152+154+169+170+155+168+160 )
≈161cm
B组: × (160+160+170+158+170+168+158+170+158
+160+160+168)
≈163cm
分析:分别计算两组的平均身高(精确到1cm)
3.1 平均数(1)
小明的身高一定比小丽矮吗?
不一定.平均身高表示一组数据
的“平均水平”.
通常,平均数可以用来表示一组数据的“平均水平”.
一般地,如果有n 个数
那么
叫做这 n 个数的算术平均数,简称平均数,
读作
“x 拔”.
3.1 平均数(1)
.
= × (159+164+160+152+154+169+170+155+168+160 )
≈161cm
= × (160+160+170+158+170+168+158+170+158
+160+160+168)
≈163cm
xA
xB
解:A组同学的平均身高:
B组同学的平均身高:
以上计算平均身高的计算过程还可以进一步简化吗?说一说你的想法.
3.1 平均数(1)
探究一
小丽用下面的办法计算B组的平均身高: B组(12人)/cm:
身高/cm
158
160
168
170
划记
频数
3 4 2 3
=
158×3+160×4+168×2+170×3
3+4+2+3
≈163(cm)
160,160,170,158,170,168,158,170,158,160,160,168
xB
说说小丽这样做的理由.
当一组数据中的若干个数据多次重复出现时可以考虑简便算法.
一般的:如果在n个数中,x1出现f1次,x2出现f2次, …,xk出现fk次,(这里f1+f2+…+fk=n),
那么x=
x1f1+x2f2+…+xkfk
n
平均数的计算方法2:
小明用下面的办法计算A组的平均身高
A组(10人)/cm:159,164,160,152,154,169,170,155,168,160
观察:这组数据都在 左右波动
160
①先将各个数据同时减去160,得到一组新数据:
-1、 4 、 0、 -8、 -6、9、 10、 -5、 8、 0
②再计算这组数据的平均数,得:
x’= (-1+4+0-8-6+9+10-5+8+0) =1.1
10
1
于是,平均身高x=x’+160=161.1≈161 (cm)
③
探究二
说说小明这样做的理由.
一般地,当一组数据 都接近同一个数据a时,可将各数据同时减去这个数a,得到一组新的数据
那么
因此
a
x
x
a
x
x
a
x
x
n
n
-
=
?
-
=
?
-
=
?
,
,
,
2
2
1
1
L
分步计算法
平均数的计算方法3:
某体操队20名队员的身高如下(单位:cm)
172,170,169,172,162,167,168,165,172,170,160,
175,168,165,171,169,167,174,170,164.
计算这些队员的平均身高.(精确到1cm)
解:①取一个常数170,以上数据同时减去170得到一
组新数据:2、0、-1、2、-8、-3、-2、-5、2、0、
-10、5、-2、-5、1、-1、-3、4、0、-6
x′=-1.5
x=170-1.5=168.5≈169(cm)
②计算这组新数据的平均数:
③原数据的平均数:
例题1
例题2
设有甲、乙、丙三种可混合包装的食品,它们的单价分别是1.8元,2.5元,3.2元,现取甲种食品50公斤,乙种食品40公斤,丙种食品10公斤,把这三种食品混合后每公斤的单价是多少?
1. 小明本周每天睡眠时间如下8,9,7,9,7,8,8,则本周小明的平均睡眠时间是 小时.
2. 一组数据85,80,x,90,它的平均数是85,求x值.
课堂练习
(85+80+x+90)
=85
x =85
8
×
方程思想
3. 11人出去采集标本,其中每人采6件的有2人,每人采3件的有4人,每人采4件的5人,求平均每人采集标本数.
×(6×2+3×4+ 4×5)
=4
已知:数据X1,X2, …,Xn的平均数为 X(以下填空用X的代数式表示)
⑴则X1+1, X2+1 … Xn+1的平均数为
⑵则X1-2, X2-2 … Xn-2的平均数为
⑶则3X1, 3X2 … 3Xn的平均数为
X+1
3X
X-2
拓展与延伸:
归纳:如果两组数据x1,x2,…,xn和y1,y2,…,yn的平均数分别是x和y,
则新数据ax1,ax2,…,axn的平均数是ax,
新数据x1+y1,x2+y2,…,xn+yn的平均数是x+y
算术平均数:在统计里,平均数是重要概念之一,它表示一组数据的”平均水平”.
公式:
(1)
(2)
(3)
注意:区别这三个公式的解题中的应用,以达到简化计算为目的地有选择地进行应用。
3.1 平均数(1)
体操比赛7位裁判给某选手的打分如下:
9.8,9.5,9.5 ,9.5,9.3,9.2,8.5.
计算这位选手的平均得分.
例题
3.1 平均数(1)
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
