第三单元 系统与设计 第二节 系统的分析(39张幻灯片)
文档属性
| 名称 | 第三单元 系统与设计 第二节 系统的分析(39张幻灯片) |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 通用技术 | ||
| 更新时间 | 2011-06-01 22:25:56 | ||
图片预览










文档简介
(共53张PPT)
经典结构的欣赏
第三单元 系统与设计
第二节 系统的分析
在日常生活中,每个人都会面临选择、面临决策,那么决策方法有那些呢?
决策方法有经验决策和科学决策;
系统分析是一种科学决策的方法。
这种为了发挥系统的功能,实现系统的目标,运用科学的方法对系统加以周详的考察、分析、比较、试验,并在此基础上拟定一套有效的处理步骤和程序,或对原有的系统提出改进方案的过程,就是系统分析。
1.什么是系统分析
2.系统分析的显著特点:
是完整地而不是零星地处理问题,考虑各种主要变化因素及其相互的影响,全面地思考和解决完问题。
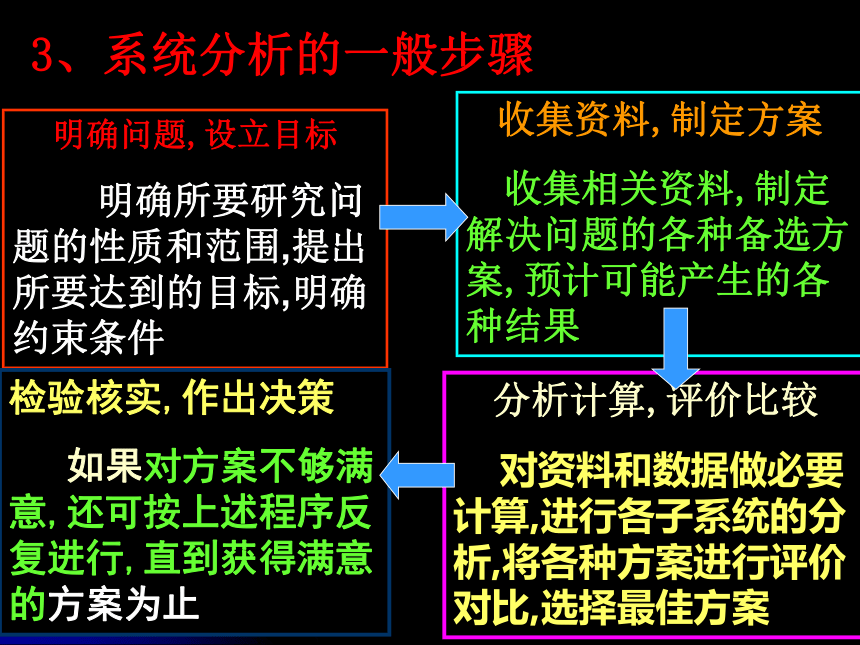
明确问题,设立目标
明确所要研究问题的性质和范围,提出所要达到的目标,明确约束条件
收集资料,制定方案
收集相关资料,制定解决问题的各种备选方案,预计可能产生的各种结果
分析计算,评价比较
对资料和数据做必要计算,进行各子系统的分析,将各种方案进行评价对比,选择最佳方案
检验核实,作出决策
如果对方案不够满意,还可按上述程序反复进行,直到获得满意的方案为止
3、系统分析的一般步骤
案例分析
田忌赛马
田忌赛马(1)
齐国的大将田忌,很喜欢赛马,有一回,他和齐王约定,要进行一场比赛。 他们商量好,把各自的马分成上,中,下三等。比赛的时候,要上马对上马,中马对中马,下马对下马。由于齐王每个等级的马都比田忌的马强得多,所以比赛了几次,田忌都失败了。 田忌觉得很扫兴,比赛还没有结束,就垂头丧气地离开赛马场。这时,田忌抬头一看,人群中有个人,原来是自己的好朋友孙膑。孙膑招呼田忌过来,拍着他的肩膀说: “我刚才看了赛马,齐王的马比你的马快不了多少呀。” 孙膑还没有说完,田忌瞪了他一眼: “想不到你也来挖苦我!” 孙膑说:“我不是挖苦你,我是说你再同他赛一次,我有办法准能让你赢了他。” 田忌疑惑地看着孙膑: “你是说另换一匹马来?” 孙膑摇摇头说: “连一匹马也不需要更换。
田忌赛马(2)
齐王屡战屡胜,正在得意洋洋地夸耀自己马匹的时候,看见田忌陪着孙膑迎面走来,便站起来讥讽地说: “怎么,莫非你还不服气?” 田忌说:“当然不服气,咱们再赛一次!”说着,“哗啦”一声,把一大堆银钱倒在桌子上,作为他下的赌钱。 齐王一看,心里暗暗好笑,于是吩咐手下,把前几次赢得的银钱全部抬来,另外又加了一千两黄金,也放在桌子上。齐王轻蔑地说:“那就开始吧!” 一声锣响,比赛开始了。 比赛的结果是三局两胜,当然是田忌赢了齐王。 还是同样的马匹,由于调换一下比赛的出场顺序,就得到转败为胜的结果。
田忌赛马战术的系统分析
1:明确问题,设立目标
问题:赛马比赛,
目标:取得比赛胜利,
约束条件:三匹马参加比赛,每匹马比赛一次。
2:收集资料,制定方案
4:检验核实,作出决策
选择合适的马的出场顺序。
3:分析计算,评价比较
孙膑所出的主意,为什么能使田忌赢得胜利?
田忌赛马能转败为胜与马、孙膑、田忌、齐威王这四个因素有关,他们是缺一不可的。
但主要是由于孙膑的原因。
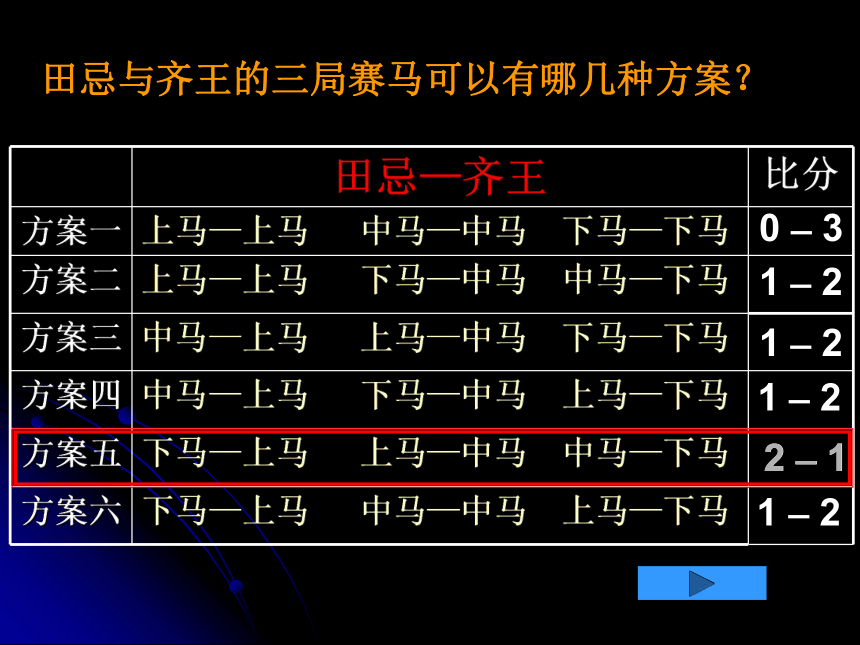
田忌与齐王的三局赛马可以有哪几种方案?
田忌—齐王 比分
方案一 上马—上马 中马—中马 下马—下马
方案二 上马—上马 下马—中马 中马—下马
方案三 中马—上马 上马—中马 下马—下马
方案四 中马—上马 下马—中马 上马—下马
方案五 下马—上马 上马—中马 中马—下马
方案六 下马—上马 中马—中马 上马—下马
0 _ 3
1 _ 2
1 _ 2
1 _ 2
1 _ 2
2 _ 1
2 _ 1
智力小游戏:三个商人和三个怪兽准备过河,但是船每次最多允许两人乘坐,空船不会行驶,且河岸的任意一侧若怪兽数量多于商人数量,商人就会被吃掉。请你设计一个方案怎样才能使商人顺利过河?
运用系统分析的方法处理具体问题时要遵循系统分析的主要原则。
4、系统分析的主要原则
整体性原则
科学性原则
综合性原则
1)整体性原则
系统分析首先着眼于系统整体,要先分析整体,在分析部分;先看全局,后看局部;先看全过程,再看某一阶段;先看长远,再看当前。
分析系统首先要着眼于系统整体:
先分析整体,再分析部分
先看全局,后看局部
先看全过程,再看某一个阶段
先看长远,再看当前
1)整体性原则
宋真宗在位时,皇宫曾起火。一夜之间,大片的宫室楼台殿阁亭榭变成了废墟。为了修复这些宫殿,宋真宗派当时的晋国公丁谓主持修缮工程。
当时,要完成这项重大的建筑工程,面临着三个大问题:
第一,需要把大量的废墟垃圾清理掉;
第二,要运来大批木材和石料;
第三,要运来大量新土。
丁谓研究了工程之后,制订了这样的施工方案:
首先,从施工现场向外挖了若干条大深沟,把挖出来的土作为施工需要的新土备用,于是就解决了新土问题。
第二步,从城外把汴水引入所挖的大沟中,于是就可以利用木排及船只运送木材石料,解决了木材石料的运输问题。
最后,等到材料运输任务完成之后,再把沟中的水排掉,把工地上的垃圾填入沟内,使沟重新变为平地。
简单归纳起来,就是这样一个过程:
挖沟(取土)→引水入沟(水道运输)→填沟(处理垃圾)。
按照这个施工方案,不仅节约了许多时间和经费,而且使工地秩序井然,使城内的交通和生活秩序不受施工太大的影响,因而确实是很科学的施工方案。
丁谓在修复皇宫工程中,运用了整体的解决方案,使取土、运输材料、处理垃圾三项繁重的任务协调起来,在总体上得到了最佳解决。
赵明同学家所在街道的人行道在一年内进行了三次施工,分别是电信部门铺设通讯线路、煤气公司预埋煤气管道、市政部门维修下水管道,结果重复施工,造成了人力和财力资源的浪费,同时也给市民带来了不便。
马上行动
请分析这一事件的问题所在,你认为怎样处理更为合理?
马上行动
这一事件的原因在于,电信部门、煤气公司、市政部门三家没有统一协调,造成了各自封闭的局面。各部门只根据自己的时间进行施工。没有从全局着眼,缺少整体统筹的观念,给市民带来了不便。好的处理办法是,三家共同协商,一次性地解决问题。
2)科学性原则
系统分析一方面要有严格的工作步骤,另一方面尽可能地运用科学方法和数学工具进行定量分析,使决策的过程和结果更具说服力。
例如,在比较种稻是一年三季合算还是一年两季合算时,有人就提出“三三进九不如二五一十”,这就是最简单而且也是最实用的定量分析。当然,在处理复杂系统的分析和优化问题时,往往需要使用比较复杂的数学工具。
科学性原则
系统分析总是为实现系统目标服务的,当系统存在若干个目标时,应将目标排出优先次序,首先选取最优先的目标,然后尽可能在不损害第一目标的前提下完成下一个目标,这就需要综合分析、统筹兼顾、不可顾此失彼,因小失大。
3)综合性原则
例如,工业生产既要求产量大,又要求质量好、成本低,如果片面强调一方面就会产生偏差;城市公交系统既要强化公共交通的安全,又要缩短车辆行驶的时间,实现社会效益和经济效益双丰收。
目标函数:
约束条件:
影响因素:
目标与收益总和之间的关系
对目标函数起限制作用,不能人为调节
产生影响,可人为调节。
进行系统优化应考虑的三个要素
案例
某家具厂要安排一周的计划,产品是桌子和椅子。制作一张桌子需4平方木板及20小时工时,制作一张椅子需6平方木板及18小时工时;每周拥有木材板料600平方,可用工时400小时;每张桌子利润50元,每只椅子利润60元。按合同每周至少要交付8张桌子和5张椅子,假定所有产品都能销售。问:该厂每周生产桌子和椅子的数量分别是多少时,能获得最大利润?
生产利润问题
产品 需木料 需工时 利润 计划产量
桌子 4 20 50
椅子 6 18 60
受约束因素 约束内容
木料 最多600
工时 最多400个
桌子 至少8张
椅子 至少5把
利润问题
目标:家具销售获取最大利润
约束条件:材料、劳动力、合同
影响因素:桌子数量x1、椅子数量x2 。(决策变量)
三个要素
目标函数:Smax=50x1+60 x2
约束条件:4x1+6 x2≤600(材料)
20 x1+18 x2≤400(工时)
x1≥8 , x2≥5(合同)
最优方案:
建立关系:
生产利润问题
Smax=50X1+60X2
约束条件
(1)4X1+6X2≤ 600
(2)20X1+18X2≤ 400
(3)X1≥ 8
(4)X2≥ 5
我们列出了一个目标函数和四个约束条件,实际上我们已经建立了一个数学模型。
我们通过数学模型,计算出的目标值是每周获取的最大利润,所得到的就是最优解:每周生产桌子数量是X1、生产椅子的数量是X2)。
对于比较复杂的系统,人们对其特征了解不够,所以需要运用一定的数学的手段描述它,进而找到合适的解决方案。
为使系统达到最优的目标而提出的求解方法称为最优化方法。系统优化的方法是多样的,有的运用数学模型求解,有的通过科学的估算、试验等方法实现。但无论运用怎样的优化方法,都需要经过若干次完善和验证,才能得出最优解或满意解。
系统的优化
数学模型
估算、试验
最优解
满意解
完善、验证
一、明确问题,设立目标
施工项目: A、B、C三栋教学楼装修
约束条件:依次分为水电、木工、油漆三个施工过程,每个施工过程需要3周时间
目标:组织装修,使装修工期和资源利用最为合理。
二、收集资料,制定方案
方案一:按照施工要求,从A到B到C,依此进行施工
方案二:按照施工要求,A、B、C栋同时进行施工
方案三:按照施工要求,A、B、C栋进行流水施工
四、检验核实,确定方案
三、分析计算,评价比较
各种方案比较
选择出最佳方案:方案三
装修施工的组织优化
方案一
楼 装修
过程 工期 装修施工进度(周)
3 6 9 12 15 18 21 24 27
A 水电 3
木工 3
油漆 3
B 水电 3
木工 3
油漆 3
C 水电 3
木工 3
油漆 3
■
■
■
■
■
■
■
■
■
方案二
楼 装修
过程 工期 装修施工进度(周)
3 6 9 12 15 18 21 24 27
A 水电 3
木工 3
油漆 3
B 水电 3
木工 3
油漆 3
C 水电 3
木工 3
油漆 3
■
■
■
■
■
■
■
■
■
方案三
楼 装修
过程 工期 装修施工进度(周)
3 6 9 12 15 18 21 24 27
A 水电 3
木工 3
油漆 3
B 水电 3
木工 3
油漆 3
C 水电 3
木工 3
油漆 3
■
■
■
■
■
■
■
■
■
方案比较
施工特点 工期 施工队 设备、材料 现场管理
方案一
方案二
方案三
依次施工
27周
1
投入少
简单
平行施工
9周
3
投入多
复杂
流水施工
15周
1
较多
较简单
思考
在装修施工的组织优化中,影响优化的主要因素有哪些?
影响优化的主要因素有施工时间、装修队伍数量、设备的数量、管理能力等。
实现系统的最优化,就可以在一定资源条件下,取得最佳的经济效果,而投入的人力、物力、财力达到最小。
2)系统优化的意义
再见
经典结构的欣赏
第三单元 系统与设计
第二节 系统的分析
在日常生活中,每个人都会面临选择、面临决策,那么决策方法有那些呢?
决策方法有经验决策和科学决策;
系统分析是一种科学决策的方法。
这种为了发挥系统的功能,实现系统的目标,运用科学的方法对系统加以周详的考察、分析、比较、试验,并在此基础上拟定一套有效的处理步骤和程序,或对原有的系统提出改进方案的过程,就是系统分析。
1.什么是系统分析
2.系统分析的显著特点:
是完整地而不是零星地处理问题,考虑各种主要变化因素及其相互的影响,全面地思考和解决完问题。
明确问题,设立目标
明确所要研究问题的性质和范围,提出所要达到的目标,明确约束条件
收集资料,制定方案
收集相关资料,制定解决问题的各种备选方案,预计可能产生的各种结果
分析计算,评价比较
对资料和数据做必要计算,进行各子系统的分析,将各种方案进行评价对比,选择最佳方案
检验核实,作出决策
如果对方案不够满意,还可按上述程序反复进行,直到获得满意的方案为止
3、系统分析的一般步骤
案例分析
田忌赛马
田忌赛马(1)
齐国的大将田忌,很喜欢赛马,有一回,他和齐王约定,要进行一场比赛。 他们商量好,把各自的马分成上,中,下三等。比赛的时候,要上马对上马,中马对中马,下马对下马。由于齐王每个等级的马都比田忌的马强得多,所以比赛了几次,田忌都失败了。 田忌觉得很扫兴,比赛还没有结束,就垂头丧气地离开赛马场。这时,田忌抬头一看,人群中有个人,原来是自己的好朋友孙膑。孙膑招呼田忌过来,拍着他的肩膀说: “我刚才看了赛马,齐王的马比你的马快不了多少呀。” 孙膑还没有说完,田忌瞪了他一眼: “想不到你也来挖苦我!” 孙膑说:“我不是挖苦你,我是说你再同他赛一次,我有办法准能让你赢了他。” 田忌疑惑地看着孙膑: “你是说另换一匹马来?” 孙膑摇摇头说: “连一匹马也不需要更换。
田忌赛马(2)
齐王屡战屡胜,正在得意洋洋地夸耀自己马匹的时候,看见田忌陪着孙膑迎面走来,便站起来讥讽地说: “怎么,莫非你还不服气?” 田忌说:“当然不服气,咱们再赛一次!”说着,“哗啦”一声,把一大堆银钱倒在桌子上,作为他下的赌钱。 齐王一看,心里暗暗好笑,于是吩咐手下,把前几次赢得的银钱全部抬来,另外又加了一千两黄金,也放在桌子上。齐王轻蔑地说:“那就开始吧!” 一声锣响,比赛开始了。 比赛的结果是三局两胜,当然是田忌赢了齐王。 还是同样的马匹,由于调换一下比赛的出场顺序,就得到转败为胜的结果。
田忌赛马战术的系统分析
1:明确问题,设立目标
问题:赛马比赛,
目标:取得比赛胜利,
约束条件:三匹马参加比赛,每匹马比赛一次。
2:收集资料,制定方案
4:检验核实,作出决策
选择合适的马的出场顺序。
3:分析计算,评价比较
孙膑所出的主意,为什么能使田忌赢得胜利?
田忌赛马能转败为胜与马、孙膑、田忌、齐威王这四个因素有关,他们是缺一不可的。
但主要是由于孙膑的原因。
田忌与齐王的三局赛马可以有哪几种方案?
田忌—齐王 比分
方案一 上马—上马 中马—中马 下马—下马
方案二 上马—上马 下马—中马 中马—下马
方案三 中马—上马 上马—中马 下马—下马
方案四 中马—上马 下马—中马 上马—下马
方案五 下马—上马 上马—中马 中马—下马
方案六 下马—上马 中马—中马 上马—下马
0 _ 3
1 _ 2
1 _ 2
1 _ 2
1 _ 2
2 _ 1
2 _ 1
智力小游戏:三个商人和三个怪兽准备过河,但是船每次最多允许两人乘坐,空船不会行驶,且河岸的任意一侧若怪兽数量多于商人数量,商人就会被吃掉。请你设计一个方案怎样才能使商人顺利过河?
运用系统分析的方法处理具体问题时要遵循系统分析的主要原则。
4、系统分析的主要原则
整体性原则
科学性原则
综合性原则
1)整体性原则
系统分析首先着眼于系统整体,要先分析整体,在分析部分;先看全局,后看局部;先看全过程,再看某一阶段;先看长远,再看当前。
分析系统首先要着眼于系统整体:
先分析整体,再分析部分
先看全局,后看局部
先看全过程,再看某一个阶段
先看长远,再看当前
1)整体性原则
宋真宗在位时,皇宫曾起火。一夜之间,大片的宫室楼台殿阁亭榭变成了废墟。为了修复这些宫殿,宋真宗派当时的晋国公丁谓主持修缮工程。
当时,要完成这项重大的建筑工程,面临着三个大问题:
第一,需要把大量的废墟垃圾清理掉;
第二,要运来大批木材和石料;
第三,要运来大量新土。
丁谓研究了工程之后,制订了这样的施工方案:
首先,从施工现场向外挖了若干条大深沟,把挖出来的土作为施工需要的新土备用,于是就解决了新土问题。
第二步,从城外把汴水引入所挖的大沟中,于是就可以利用木排及船只运送木材石料,解决了木材石料的运输问题。
最后,等到材料运输任务完成之后,再把沟中的水排掉,把工地上的垃圾填入沟内,使沟重新变为平地。
简单归纳起来,就是这样一个过程:
挖沟(取土)→引水入沟(水道运输)→填沟(处理垃圾)。
按照这个施工方案,不仅节约了许多时间和经费,而且使工地秩序井然,使城内的交通和生活秩序不受施工太大的影响,因而确实是很科学的施工方案。
丁谓在修复皇宫工程中,运用了整体的解决方案,使取土、运输材料、处理垃圾三项繁重的任务协调起来,在总体上得到了最佳解决。
赵明同学家所在街道的人行道在一年内进行了三次施工,分别是电信部门铺设通讯线路、煤气公司预埋煤气管道、市政部门维修下水管道,结果重复施工,造成了人力和财力资源的浪费,同时也给市民带来了不便。
马上行动
请分析这一事件的问题所在,你认为怎样处理更为合理?
马上行动
这一事件的原因在于,电信部门、煤气公司、市政部门三家没有统一协调,造成了各自封闭的局面。各部门只根据自己的时间进行施工。没有从全局着眼,缺少整体统筹的观念,给市民带来了不便。好的处理办法是,三家共同协商,一次性地解决问题。
2)科学性原则
系统分析一方面要有严格的工作步骤,另一方面尽可能地运用科学方法和数学工具进行定量分析,使决策的过程和结果更具说服力。
例如,在比较种稻是一年三季合算还是一年两季合算时,有人就提出“三三进九不如二五一十”,这就是最简单而且也是最实用的定量分析。当然,在处理复杂系统的分析和优化问题时,往往需要使用比较复杂的数学工具。
科学性原则
系统分析总是为实现系统目标服务的,当系统存在若干个目标时,应将目标排出优先次序,首先选取最优先的目标,然后尽可能在不损害第一目标的前提下完成下一个目标,这就需要综合分析、统筹兼顾、不可顾此失彼,因小失大。
3)综合性原则
例如,工业生产既要求产量大,又要求质量好、成本低,如果片面强调一方面就会产生偏差;城市公交系统既要强化公共交通的安全,又要缩短车辆行驶的时间,实现社会效益和经济效益双丰收。
目标函数:
约束条件:
影响因素:
目标与收益总和之间的关系
对目标函数起限制作用,不能人为调节
产生影响,可人为调节。
进行系统优化应考虑的三个要素
案例
某家具厂要安排一周的计划,产品是桌子和椅子。制作一张桌子需4平方木板及20小时工时,制作一张椅子需6平方木板及18小时工时;每周拥有木材板料600平方,可用工时400小时;每张桌子利润50元,每只椅子利润60元。按合同每周至少要交付8张桌子和5张椅子,假定所有产品都能销售。问:该厂每周生产桌子和椅子的数量分别是多少时,能获得最大利润?
生产利润问题
产品 需木料 需工时 利润 计划产量
桌子 4 20 50
椅子 6 18 60
受约束因素 约束内容
木料 最多600
工时 最多400个
桌子 至少8张
椅子 至少5把
利润问题
目标:家具销售获取最大利润
约束条件:材料、劳动力、合同
影响因素:桌子数量x1、椅子数量x2 。(决策变量)
三个要素
目标函数:Smax=50x1+60 x2
约束条件:4x1+6 x2≤600(材料)
20 x1+18 x2≤400(工时)
x1≥8 , x2≥5(合同)
最优方案:
建立关系:
生产利润问题
Smax=50X1+60X2
约束条件
(1)4X1+6X2≤ 600
(2)20X1+18X2≤ 400
(3)X1≥ 8
(4)X2≥ 5
我们列出了一个目标函数和四个约束条件,实际上我们已经建立了一个数学模型。
我们通过数学模型,计算出的目标值是每周获取的最大利润,所得到的就是最优解:每周生产桌子数量是X1、生产椅子的数量是X2)。
对于比较复杂的系统,人们对其特征了解不够,所以需要运用一定的数学的手段描述它,进而找到合适的解决方案。
为使系统达到最优的目标而提出的求解方法称为最优化方法。系统优化的方法是多样的,有的运用数学模型求解,有的通过科学的估算、试验等方法实现。但无论运用怎样的优化方法,都需要经过若干次完善和验证,才能得出最优解或满意解。
系统的优化
数学模型
估算、试验
最优解
满意解
完善、验证
一、明确问题,设立目标
施工项目: A、B、C三栋教学楼装修
约束条件:依次分为水电、木工、油漆三个施工过程,每个施工过程需要3周时间
目标:组织装修,使装修工期和资源利用最为合理。
二、收集资料,制定方案
方案一:按照施工要求,从A到B到C,依此进行施工
方案二:按照施工要求,A、B、C栋同时进行施工
方案三:按照施工要求,A、B、C栋进行流水施工
四、检验核实,确定方案
三、分析计算,评价比较
各种方案比较
选择出最佳方案:方案三
装修施工的组织优化
方案一
楼 装修
过程 工期 装修施工进度(周)
3 6 9 12 15 18 21 24 27
A 水电 3
木工 3
油漆 3
B 水电 3
木工 3
油漆 3
C 水电 3
木工 3
油漆 3
■
■
■
■
■
■
■
■
■
方案二
楼 装修
过程 工期 装修施工进度(周)
3 6 9 12 15 18 21 24 27
A 水电 3
木工 3
油漆 3
B 水电 3
木工 3
油漆 3
C 水电 3
木工 3
油漆 3
■
■
■
■
■
■
■
■
■
方案三
楼 装修
过程 工期 装修施工进度(周)
3 6 9 12 15 18 21 24 27
A 水电 3
木工 3
油漆 3
B 水电 3
木工 3
油漆 3
C 水电 3
木工 3
油漆 3
■
■
■
■
■
■
■
■
■
方案比较
施工特点 工期 施工队 设备、材料 现场管理
方案一
方案二
方案三
依次施工
27周
1
投入少
简单
平行施工
9周
3
投入多
复杂
流水施工
15周
1
较多
较简单
思考
在装修施工的组织优化中,影响优化的主要因素有哪些?
影响优化的主要因素有施工时间、装修队伍数量、设备的数量、管理能力等。
实现系统的最优化,就可以在一定资源条件下,取得最佳的经济效果,而投入的人力、物力、财力达到最小。
2)系统优化的意义
再见
