沪科版八年级下册数学18.1 勾股定理(1) 课件 (共17张PPT)
文档属性
| 名称 | 沪科版八年级下册数学18.1 勾股定理(1) 课件 (共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-13 10:11:14 | ||
图片预览




文档简介
(共17张PPT)
18.1 勾股定理(1)
1.了解勾股定理的发现过程,掌握勾股定理的内容并会用面积法证明勾股定理.
2.运用勾股定理,已知直角三角形的两边求第三边的长.
3.培养学生良好的探究习惯,体会数形结合的数学思想.
学习目标
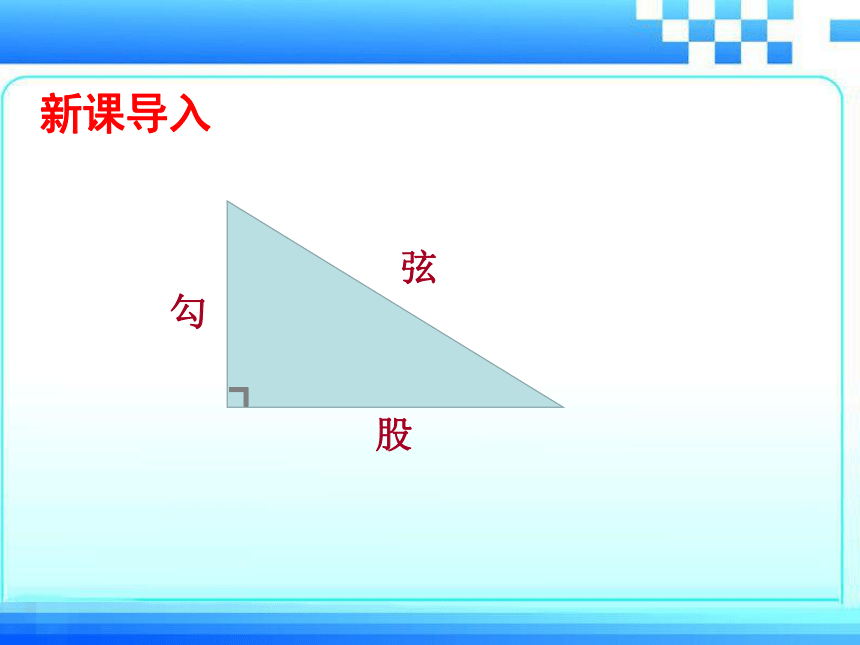
勾
股
弦
┏
新课导入
1.了解勾股定理的发现过程,掌握勾股定理的内容并会用面积法证明勾股定理.
2.运用勾股定理,已知直角三角形的两边求第三边的长.
学习目标
自助探究
自学教材内容,尝试解决下列问题:
1.等腰直角三角形的三边之间有什么关系?
2.一般的直角三角形的三边之间也有这个性质吗?如果有,可以写成什么?
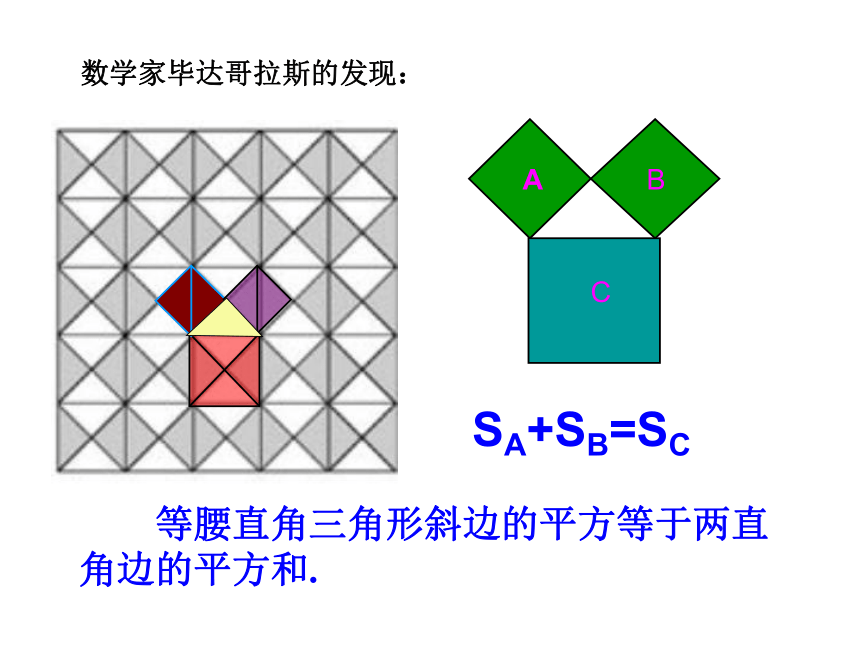
数学家毕达哥拉斯的发现:
SA+SB=SC
等腰直角三角形斜边的平方等于两直角边的平方和.
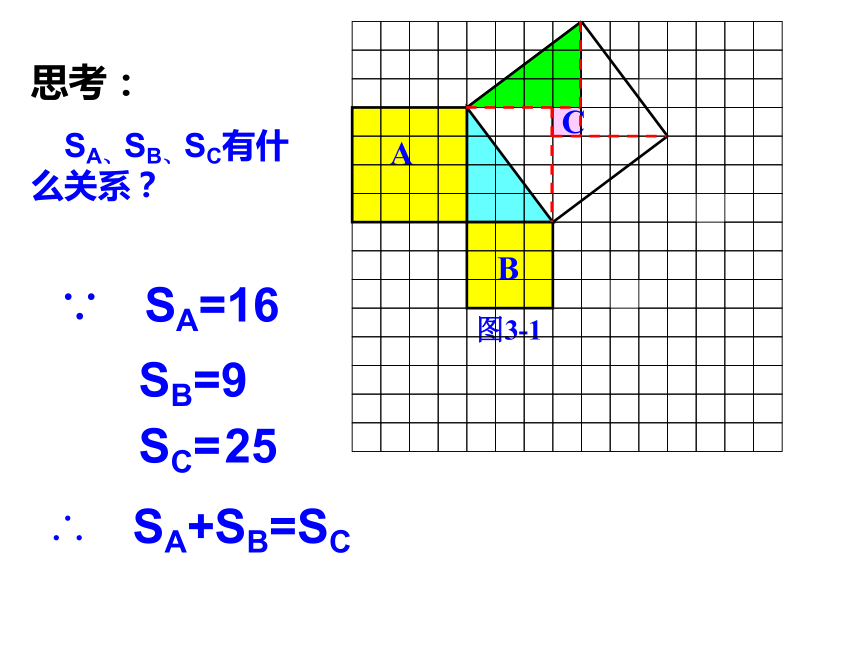
思考:
SA、SB、SC有什么关系?
SC=
∴ SA+SB=SC
SB=9
∵ SA=16
25
以直角三角形两直角边为边长的正方形面积之和等于以斜边为边长的正方形面积.
思考:
SA、SB、SC
∵ SA=6
SB=9
SC=25
∴ SA+SB=SC
b
a
c
∴ a2+b2=c2
∵ SA+SB=SC
设直角三角形的两条直角边长分别是a、b、斜边长为c,
互助交流
4个
的面积+中间小正方形的面积=该图案的面积.
直角三角形
即:4×
+(
)2=c2,
ab
b-a
化简后得:a2+b2=c2
目标检测
1.设直角三角形的两直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
2.Rt△ABC中,AB=4,AC=3,则BC的长是多少?
25
169
B
B
A
C
1.如图,字母B所代表的正方形的面积是(
)
A、12
B、13
C、144
D、194
目标检测
C
课堂小结
目标回顾:1.了解勾股定理的发现过程,掌握勾股定理的内容并会用面积法证明勾股定理.
2.运用勾股定理,已知直角三角形的两边求第三边的长.
小结反思:
补助拓展
1.在△ABC中,∠C=90°,若a=3,b=4,求斜边c上的高.
2.一直角三角形的斜边长比一条直角边长多2,另一直角边长为6,求斜边长.
1.(必做题)习题18.1复习巩固第7、8题.
2.(选做题)习题18.1复习巩固第13题.
谢谢合作!
18.1 勾股定理(1)
1.了解勾股定理的发现过程,掌握勾股定理的内容并会用面积法证明勾股定理.
2.运用勾股定理,已知直角三角形的两边求第三边的长.
3.培养学生良好的探究习惯,体会数形结合的数学思想.
学习目标
勾
股
弦
┏
新课导入
1.了解勾股定理的发现过程,掌握勾股定理的内容并会用面积法证明勾股定理.
2.运用勾股定理,已知直角三角形的两边求第三边的长.
学习目标
自助探究
自学教材内容,尝试解决下列问题:
1.等腰直角三角形的三边之间有什么关系?
2.一般的直角三角形的三边之间也有这个性质吗?如果有,可以写成什么?
数学家毕达哥拉斯的发现:
SA+SB=SC
等腰直角三角形斜边的平方等于两直角边的平方和.
思考:
SA、SB、SC有什么关系?
SC=
∴ SA+SB=SC
SB=9
∵ SA=16
25
以直角三角形两直角边为边长的正方形面积之和等于以斜边为边长的正方形面积.
思考:
SA、SB、SC
∵ SA=6
SB=9
SC=25
∴ SA+SB=SC
b
a
c
∴ a2+b2=c2
∵ SA+SB=SC
设直角三角形的两条直角边长分别是a、b、斜边长为c,
互助交流
4个
的面积+中间小正方形的面积=该图案的面积.
直角三角形
即:4×
+(
)2=c2,
ab
b-a
化简后得:a2+b2=c2
目标检测
1.设直角三角形的两直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
2.Rt△ABC中,AB=4,AC=3,则BC的长是多少?
25
169
B
B
A
C
1.如图,字母B所代表的正方形的面积是(
)
A、12
B、13
C、144
D、194
目标检测
C
课堂小结
目标回顾:1.了解勾股定理的发现过程,掌握勾股定理的内容并会用面积法证明勾股定理.
2.运用勾股定理,已知直角三角形的两边求第三边的长.
小结反思:
补助拓展
1.在△ABC中,∠C=90°,若a=3,b=4,求斜边c上的高.
2.一直角三角形的斜边长比一条直角边长多2,另一直角边长为6,求斜边长.
1.(必做题)习题18.1复习巩固第7、8题.
2.(选做题)习题18.1复习巩固第13题.
谢谢合作!
