沪科版八年级下册数学 18.1 勾股定理课件(共20张PPT)
文档属性
| 名称 | 沪科版八年级下册数学 18.1 勾股定理课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-13 10:26:07 | ||
图片预览







文档简介
(共20张PPT)
18.1勾股定理
学习目标:
1、掌握勾股定理.
2、学会利用勾股定理进行计算、证明与作图.
3、在定理的证明中培养拼图能力,通过问题的解决提高运算能力.
读一读:
1、我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.左图就是弦图,最早由三国时期赵爽在《周髀算经》中给出.右图就是北京2002年数学家大会会徽,就是此弦图。
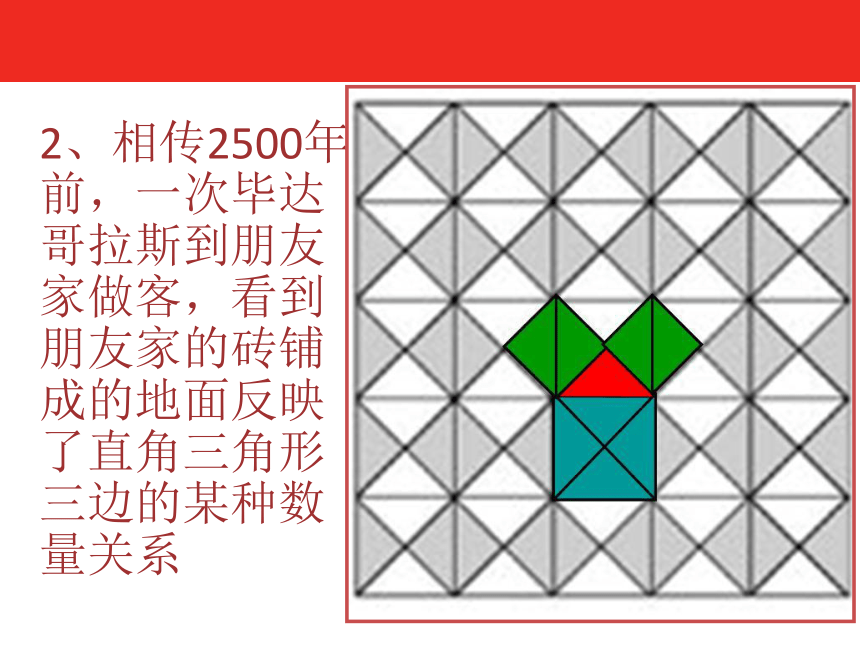
2、相传2500年前,一次毕达哥拉斯到朋友家做客,看到朋友家的砖铺成的地面反映了直角三角形三边的某种数量关系
看一看:
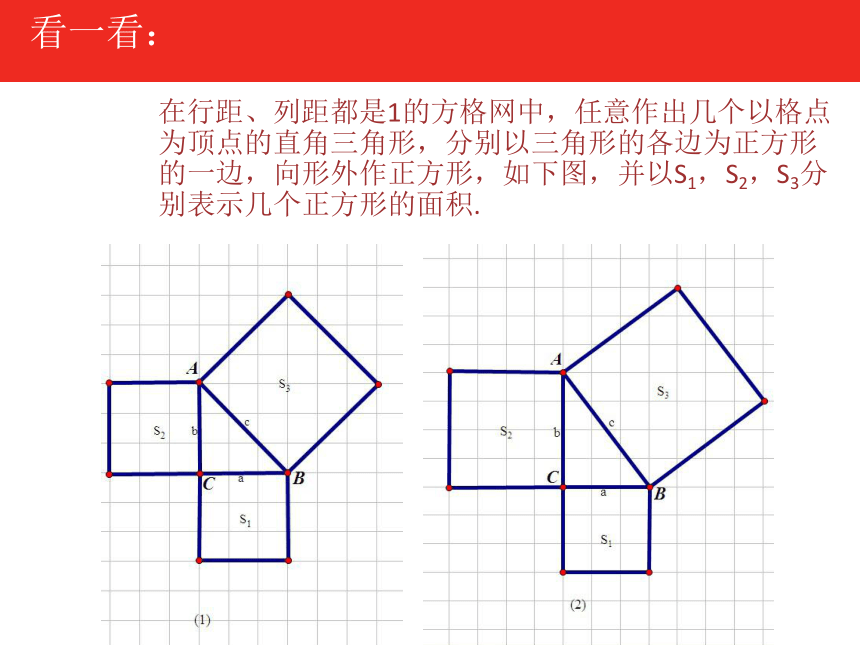
在行距、列距都是1的方格网中,任意作出几个以格点为顶点的直角三角形,分别以三角形的各边为正方形的一边,向形外作正方形,如下图,并以S1,S2,S3分别表示几个正方形的面积.
填空:
观察图(1)
S1= 个单位面积;
S2= 个单位面积;
S3= 个单位面积;
观察图(2)
S1= 个单位面积;
S2= 个单位面积;
S3= 个单位面积;
图(1)、(2)中三个正方形面积之间有怎样的关系,用:
它们的边长表示,是:
9
9
18
9
16
25
a2+b2=c2
想一想:
通过上面的探究,发现直角三角形三边的长之间有怎样的关系?
定理
直角三角形两条直角边的平方和,
等于斜边的平方.
a2+b2=c2(a、b为直角边,c为斜边)
这就是勾股定理
在国外称为毕达哥拉斯定理呦
拼一拼:
1、拿出准备好的四个全等直角三
角形(设直角边分别为a、b,斜
边为c)
2、你能用这些三角形拼成一个正
方形吗?
3、你拼的图形中有没有以c为边长的正方形呢?
4、你能否就你拼的图形说明
a2+b2=c2呢?
证明1:
如图,小正方形面积可以表示为:
还可以表示为:
∵
∴
c2
证明2:
如图,大正方形的面积可以表示为:
还可以表示为:
∵
∴
c2
结论变形:
练一练:
例题1
现有一楼房发生火灾,消防队员决定用消防车上的云梯救人,如图,已知云梯最多只能伸长到10m,消防车高3m.救人时云梯伸至最长,在完成从9m高处救人后,还要从12m高处救人,这时消防车要从原处再向着火的楼房靠近多少米?(精确到十分位)
例题2
试一试:
1、(1)长3m的梯子斜靠着墙,梯子底端离墙底0.6m,
问梯子顶端离地面多少米?
(2)题(1)中,若梯子的顶端自墙面下滑了0.9m,那么梯子的底端沿地面向外滑动的距离是否也是0.9m?说明理由.
小结:
本节课知识点
也叫毕达哥拉斯定理
家庭作业:
1、同步练习18.1(一)
2、回去思考下图如何用来证明勾股定理?
毕达哥拉斯树
感谢大家!
祝同学们学习进步!
再见!
18.1勾股定理
学习目标:
1、掌握勾股定理.
2、学会利用勾股定理进行计算、证明与作图.
3、在定理的证明中培养拼图能力,通过问题的解决提高运算能力.
读一读:
1、我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.左图就是弦图,最早由三国时期赵爽在《周髀算经》中给出.右图就是北京2002年数学家大会会徽,就是此弦图。
2、相传2500年前,一次毕达哥拉斯到朋友家做客,看到朋友家的砖铺成的地面反映了直角三角形三边的某种数量关系
看一看:
在行距、列距都是1的方格网中,任意作出几个以格点为顶点的直角三角形,分别以三角形的各边为正方形的一边,向形外作正方形,如下图,并以S1,S2,S3分别表示几个正方形的面积.
填空:
观察图(1)
S1= 个单位面积;
S2= 个单位面积;
S3= 个单位面积;
观察图(2)
S1= 个单位面积;
S2= 个单位面积;
S3= 个单位面积;
图(1)、(2)中三个正方形面积之间有怎样的关系,用:
它们的边长表示,是:
9
9
18
9
16
25
a2+b2=c2
想一想:
通过上面的探究,发现直角三角形三边的长之间有怎样的关系?
定理
直角三角形两条直角边的平方和,
等于斜边的平方.
a2+b2=c2(a、b为直角边,c为斜边)
这就是勾股定理
在国外称为毕达哥拉斯定理呦
拼一拼:
1、拿出准备好的四个全等直角三
角形(设直角边分别为a、b,斜
边为c)
2、你能用这些三角形拼成一个正
方形吗?
3、你拼的图形中有没有以c为边长的正方形呢?
4、你能否就你拼的图形说明
a2+b2=c2呢?
证明1:
如图,小正方形面积可以表示为:
还可以表示为:
∵
∴
c2
证明2:
如图,大正方形的面积可以表示为:
还可以表示为:
∵
∴
c2
结论变形:
练一练:
例题1
现有一楼房发生火灾,消防队员决定用消防车上的云梯救人,如图,已知云梯最多只能伸长到10m,消防车高3m.救人时云梯伸至最长,在完成从9m高处救人后,还要从12m高处救人,这时消防车要从原处再向着火的楼房靠近多少米?(精确到十分位)
例题2
试一试:
1、(1)长3m的梯子斜靠着墙,梯子底端离墙底0.6m,
问梯子顶端离地面多少米?
(2)题(1)中,若梯子的顶端自墙面下滑了0.9m,那么梯子的底端沿地面向外滑动的距离是否也是0.9m?说明理由.
小结:
本节课知识点
也叫毕达哥拉斯定理
家庭作业:
1、同步练习18.1(一)
2、回去思考下图如何用来证明勾股定理?
毕达哥拉斯树
感谢大家!
祝同学们学习进步!
再见!
