人教版高中物理 必修二 第六章 6.5宇宙航行(共43张PPT)
文档属性
| 名称 | 人教版高中物理 必修二 第六章 6.5宇宙航行(共43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-07-12 00:00:00 | ||
图片预览









文档简介
(共43张PPT)
5
宇宙航行
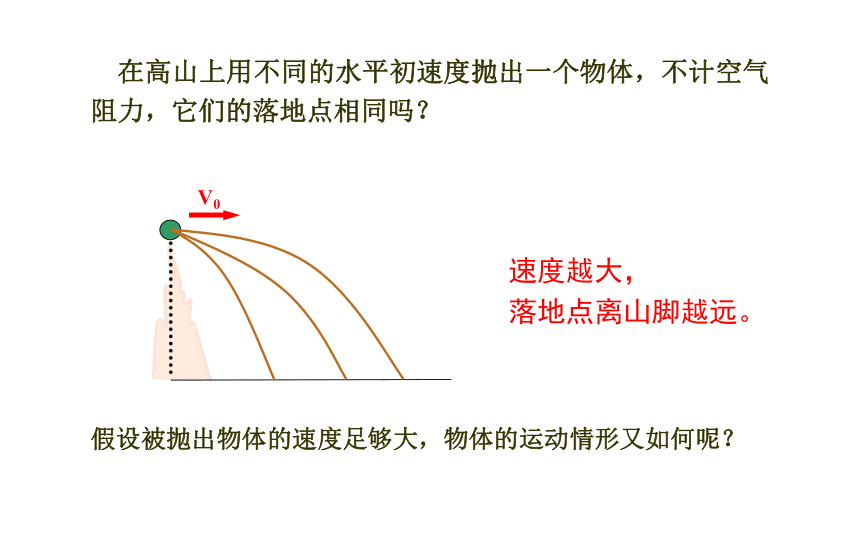
在高山上用不同的水平初速度抛出一个物体,不计空气阻力,它们的落地点相同吗?
速度越大,
落地点离山脚越远。
假设被抛出物体的速度足够大,物体的运动情形又如何呢?
V0
英国科学家牛顿(1643-1727)
在1687年出版的《自然哲学的数学原理》中,牛顿设想抛出物体的速度足够大时,物体就不会落回地面。
牛顿的设想
牛顿人造卫星原理图
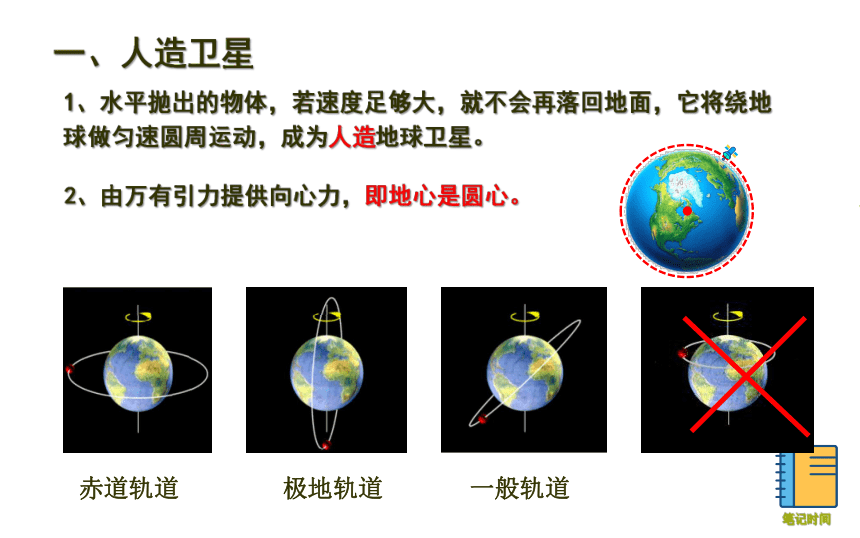
一、人造卫星
1、水平抛出的物体,若速度足够大,就不会再落回地面,它将绕地球做匀速圆周运动,成为人造地球卫星。
笔记时间
2、由万有引力提供向心力,即地心是圆心。
赤道轨道
极地轨道
一般轨道
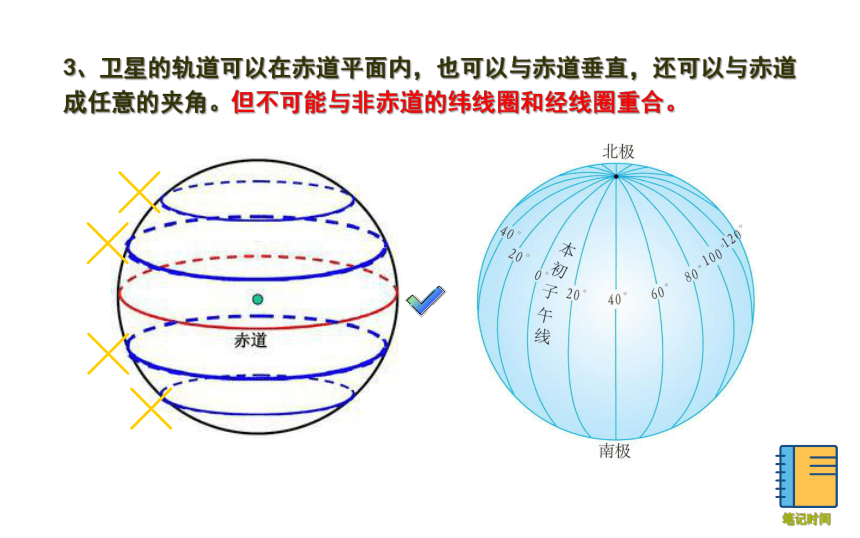
3、卫星的轨道可以在赤道平面内,也可以与赤道垂直,还可以与赤道成任意的夹角。但不可能与非赤道的纬线圈和经线圈重合。
笔记时间
(r
越大,T
越大)
(r
越大,v
越小)
(r
越大,ω越小)
可见:高轨低速长周期,低轨高速短周期
笔记时间
4、卫星运行速度、角速度、周期与半径的关系:
笔记时间
5、发射卫星(加速上升)和回收卫星(减速下降)时卫星处于超重状态;而在轨运行时处于完全失重状态,由于重力产生的一切现象均消失。
6、由于人造地球卫星的轨道半径有最小值,且rmin=R,则
rmin=R
高空空气稀薄,阻力小
【方法一】万有引力提供物体作圆周运动的向心力
【方法二】在地面附近,重力提供物体作圆周运动的向心力
那么,发射速度为多大时,物体将不会落回地面而绕着地球表面运动呢?
(已知G=6.67×10-11Nm2/kg2
,
地球质量M=5.89×1024kg,
地球半径R=6400km,地球表面重力加速度g=9.8m/s2
)
1、第一宇宙速度:
(环绕速度)物体在地面附近绕地球做匀速圆周运动的速度。
二、宇宙速度
(1)7.9km/s为卫星的最小发射速度。
向高轨道和近地轨道发射卫星,哪个难度大?需要的发射速度大?
(2)7.9km/s是卫星的最大运行速度。
高轨道卫星和近地轨道卫星相比,哪个运行速度大?
人造卫星
笔记时间
v2=11.2km/s
v3=16.7km/s
2、第二宇宙速度:
(脱离速度)使卫星挣脱地球的束缚,成为绕太阳运行的人造行星的最小发射速度。
3、第三宇宙速度:
(逃逸速度)使卫星挣脱太阳引力的束缚,飞到太阳系外的最小发射速度。
人造行星
人造恒星
笔记时间
P
V=7.9km/s
7.9km/sV>11.2km/S
探究:
若卫星的发射速度大于7.9km/s
,会怎样呢?
离开地球再也不回来
发射速度v
运动情况
v﹤7.9km/s
v=7.9km/s
7.9km/s
﹤
v
﹤11.2km/s
11.2km/s≤
v
﹤16.7km/s
16.7km/s
≤
v
落回地面
在地面附近绕地球做匀速圆周运动
绕地球做椭圆运动
物体绕太阳运动
物体飞出太阳系
(多选)关于地球的第一宇宙速度,正确的是(
)
A.它是人造地球卫星绕地球运行的最小速度
B.它是人造地球卫星在近地轨道运行的最大速度
C.它是人造地球卫星进入近地轨道的最小发射速度
D.根据人造卫星环绕地球运行的速度
,把卫星发射到越远的地方越容易
B
C
最大运行速度
轨道越高,消耗能量越多,所以越困难
(单选)如图,同一轨道平面内的三颗人造地球卫星,正确的是( )
A.
根据
,可知
vA
<
vB
<
vC
B.
根据万有引力定律,可知
FA
>
FB
>
FC
C.
角速度
wA
>
wB
>
wC
D.
向心加速度
aA
<
aB
<
aC
C
高轨低速长周期
卫星质量未知,所以无法判断
(多选)两颗人造卫星,质量比m1:m2=1:2,轨道半径之比R1:R2=3:1,不正确的是(?
)
A.周期之比T1:T2=3:1
B.线速度之比v1:v2=3:1
C.向心力之比为F1:F2=1:18
D.向心加速度之比a1:a2=1:9
A
B
三、同步卫星
1、
定义:所谓地球同步卫星,是相对于地面静止的和地球具有相同周期的卫星,同步卫星必须位于赤道平面内,且到地面的高度一定。
笔记时间
笔记时间
2、地球同步卫星的运行特征——五个“定”
①定轨道,其运行轨道平面在赤道平面内;
②定方向,即自西向东;
③定周期,即运行周期等于地球自转周期(24
h)
④定高度,即离地面高度一定(h=36000
km),
大约地球半径的6倍
⑤定角速度,与地面上的物体属于同轴传动。
笔记时间
同步卫星的应用:主要用于通信,所以有时也叫通信卫星。
3颗同步卫星可实现全球覆盖
为了卫星之间不互相干扰,大约3°左右才能放置1颗,这样地球的同步卫星只能有120颗。可见,空间位置也是一种资源。
3、地球同步卫星是联系地面上的物体与天上的卫星的桥梁
A
B
C
A是地面上的物体
B是同步卫星
C是一般卫星
同轴传动
都是卫星
笔记时间
(单选)“神舟”十号飞船在圆轨道上运转一圈的时间为90分钟,由此他将“神舟”十号飞船与同步卫星进行比较,正确的是(
)
A.“神舟”
十号飞船运行的轨道和同步卫星的轨道是同一轨道
B.“神舟”
十号飞船运行的角速度大于同步卫星的角速度
C.“神舟”
十号飞船运行的向心加速度小于同步卫星的加速度
D.“神舟”
十号飞船在圆轨道上的速率小于同步卫星的速率
B
例2:
关于地球同步卫星,下列说法正确的是(
)
A.它的运行速度小于7.9km/s
B.它的运行速度大于7.9km/s
C.它的周期是24h,且轨道平面于赤道平面重合
D.每一个地球同步卫星离开地面的高度是一样的
ACD
D
1
3
2
V
F引
F引<F向
F引>F向
M
A点速度—内小外大(在A点看轨迹)
在A点万有引力不变,变化的是向心力
A
四、变轨问题
1、
变轨:当卫星点火突然加速或者减速时,由于万有引力不再等于向心力,卫星将做近心运动或者离心运动,卫星将变轨。
①为了节省能量,在赤道上顺着地球自转方向发射卫星到近地圆轨道Ⅰ上。
③在椭圆轨道Ⅱ上的Q
点(远地点),由于万有引力大于向心力,故从Q点开始做近心运动,若再次点火加速可使万有引力等于向心力,使卫星进入圆形轨道Ⅲ做圆周运动。
2、
发射卫星——两次点火加速
②在
轨道Ⅰ上的P
点突然点火加速,由于速度变大,则需要的向心力也变大,故万有引力不足以提供在轨道Ⅰ上做圆周运动的向心力,卫星做离心运动进入椭圆轨道Ⅱ。
Ⅰ
P
Ⅱ
Q
Ⅲ
②卫星在圆形轨道Ⅲ上的Q点突然点火减速,使得万有引力大于向心力,卫星将沿着椭圆轨道Ⅱ做近心运动。
①卫星在圆形轨道Ⅲ做圆周运动。
3、
回收卫星——两次点火减速
③在椭圆轨道Ⅱ上的P
点(远地点),由于万有引力小于向心力,故从P点开始做离心运动,若再次点火减速可使万有引力等于向心力,使卫星进入圆形轨道Ⅰ做圆周运动。
Ⅰ
P
Ⅱ
Q
Ⅲ
4、总结规律
Ⅰ
P
Ⅱ
Q
Ⅲ
①线速度
②周期
③加速度
椭圆:近快远慢
圆:利用
相切点:内小外大
无论是圆还是椭圆都用:
r1
r3
2r2
无论什么位置都用:
注意:不是向心加速度
例题、如图所示,发射同步卫星时,先将卫星发射至近地圆轨道1,然后经点火使其沿椭圆轨道2运行;最后再次点火将其送入同步圆轨道3。轨道1、2相切于P点,2、3相切于Q点。当卫星分别在1、2、3上正常运行时,以下说法正确的是(
)
A、在轨道3上的速率大于1上的速率
B、在轨道3上的角速度小于1上的角速度
C、在轨道2上经过Q点时的速率等于在轨道3
上经过Q点时的速率
D、在轨道1上经过P点时的加速度等于在轨道2
上经过P点时的加速度
Q
P
2
·
3
1
BD
月球
月球轨道
地球
地月转移轨道
点火加速
减速制动
月球探测卫星发射
2.
2007年10月24日“嫦娥一号”卫星星箭分离,卫星进入绕地轨道。在绕地运行时,要经过三次近地变轨:12小时椭圆轨道①→24小时椭圆轨道②→48小时椭圆轨道③→修正轨道④→地月转移轨道⑤。11月5日11时,当卫星经过距月球表面高度为h的A点时,再经三次变轨:12小时椭圆轨道⑥→3.5小时椭圆
轨道⑦→最后进入周期为T的极月圆轨道⑧
,如图所示(
)
A.“嫦娥一号”由⑤到⑥需加速、由⑦到⑧需减速
B.发射“嫦娥一号”的速度必须达到第三宇宙速度
C.在绕月圆轨道上,卫星周期与卫星质量有关
D.卫星受月球的引力与它到月球中心距离的平方成反比
E.在绕月圆轨道上,卫星受地球的引力大于受月球的引力
①
②
③
近地变轨
轨道修正
转移轨道
④
⑤
⑥
⑦
⑧
发射
D
5、交会对接
后下方加速
前上方减速
5、交会对接
再加速
后方先减速变轨
例:在太空中有两飞行器a、b,它们在绕地球的同一圆形轨道上同向运行,a在前b在后,它都配有能沿运动方向向前或向后喷气的发动机,现要想b
尽快追上a
并完成对接,b应采取的措施是(
)
A、沿运动方向喷气
B、先沿运动方向喷气,后沿运动反方向喷气
C、沿运动反方向喷气
D、先沿运动反方向喷气,后沿运动方向喷气
B
新课学习
史上第一人
五、梦想成真—人类航天史
新课学习
理论泰斗
新课学习
女汉子不让须眉
新课学习
彪悍的人生不需要解释
新课学习
杨利伟
翟志刚
刘洋
王亚平
中国航天历程
5
宇宙航行
在高山上用不同的水平初速度抛出一个物体,不计空气阻力,它们的落地点相同吗?
速度越大,
落地点离山脚越远。
假设被抛出物体的速度足够大,物体的运动情形又如何呢?
V0
英国科学家牛顿(1643-1727)
在1687年出版的《自然哲学的数学原理》中,牛顿设想抛出物体的速度足够大时,物体就不会落回地面。
牛顿的设想
牛顿人造卫星原理图
一、人造卫星
1、水平抛出的物体,若速度足够大,就不会再落回地面,它将绕地球做匀速圆周运动,成为人造地球卫星。
笔记时间
2、由万有引力提供向心力,即地心是圆心。
赤道轨道
极地轨道
一般轨道
3、卫星的轨道可以在赤道平面内,也可以与赤道垂直,还可以与赤道成任意的夹角。但不可能与非赤道的纬线圈和经线圈重合。
笔记时间
(r
越大,T
越大)
(r
越大,v
越小)
(r
越大,ω越小)
可见:高轨低速长周期,低轨高速短周期
笔记时间
4、卫星运行速度、角速度、周期与半径的关系:
笔记时间
5、发射卫星(加速上升)和回收卫星(减速下降)时卫星处于超重状态;而在轨运行时处于完全失重状态,由于重力产生的一切现象均消失。
6、由于人造地球卫星的轨道半径有最小值,且rmin=R,则
rmin=R
高空空气稀薄,阻力小
【方法一】万有引力提供物体作圆周运动的向心力
【方法二】在地面附近,重力提供物体作圆周运动的向心力
那么,发射速度为多大时,物体将不会落回地面而绕着地球表面运动呢?
(已知G=6.67×10-11Nm2/kg2
,
地球质量M=5.89×1024kg,
地球半径R=6400km,地球表面重力加速度g=9.8m/s2
)
1、第一宇宙速度:
(环绕速度)物体在地面附近绕地球做匀速圆周运动的速度。
二、宇宙速度
(1)7.9km/s为卫星的最小发射速度。
向高轨道和近地轨道发射卫星,哪个难度大?需要的发射速度大?
(2)7.9km/s是卫星的最大运行速度。
高轨道卫星和近地轨道卫星相比,哪个运行速度大?
人造卫星
笔记时间
v2=11.2km/s
v3=16.7km/s
2、第二宇宙速度:
(脱离速度)使卫星挣脱地球的束缚,成为绕太阳运行的人造行星的最小发射速度。
3、第三宇宙速度:
(逃逸速度)使卫星挣脱太阳引力的束缚,飞到太阳系外的最小发射速度。
人造行星
人造恒星
笔记时间
P
V=7.9km/s
7.9km/s
探究:
若卫星的发射速度大于7.9km/s
,会怎样呢?
离开地球再也不回来
发射速度v
运动情况
v﹤7.9km/s
v=7.9km/s
7.9km/s
﹤
v
﹤11.2km/s
11.2km/s≤
v
﹤16.7km/s
16.7km/s
≤
v
落回地面
在地面附近绕地球做匀速圆周运动
绕地球做椭圆运动
物体绕太阳运动
物体飞出太阳系
(多选)关于地球的第一宇宙速度,正确的是(
)
A.它是人造地球卫星绕地球运行的最小速度
B.它是人造地球卫星在近地轨道运行的最大速度
C.它是人造地球卫星进入近地轨道的最小发射速度
D.根据人造卫星环绕地球运行的速度
,把卫星发射到越远的地方越容易
B
C
最大运行速度
轨道越高,消耗能量越多,所以越困难
(单选)如图,同一轨道平面内的三颗人造地球卫星,正确的是( )
A.
根据
,可知
vA
<
vB
<
vC
B.
根据万有引力定律,可知
FA
>
FB
>
FC
C.
角速度
wA
>
wB
>
wC
D.
向心加速度
aA
<
aB
<
aC
C
高轨低速长周期
卫星质量未知,所以无法判断
(多选)两颗人造卫星,质量比m1:m2=1:2,轨道半径之比R1:R2=3:1,不正确的是(?
)
A.周期之比T1:T2=3:1
B.线速度之比v1:v2=3:1
C.向心力之比为F1:F2=1:18
D.向心加速度之比a1:a2=1:9
A
B
三、同步卫星
1、
定义:所谓地球同步卫星,是相对于地面静止的和地球具有相同周期的卫星,同步卫星必须位于赤道平面内,且到地面的高度一定。
笔记时间
笔记时间
2、地球同步卫星的运行特征——五个“定”
①定轨道,其运行轨道平面在赤道平面内;
②定方向,即自西向东;
③定周期,即运行周期等于地球自转周期(24
h)
④定高度,即离地面高度一定(h=36000
km),
大约地球半径的6倍
⑤定角速度,与地面上的物体属于同轴传动。
笔记时间
同步卫星的应用:主要用于通信,所以有时也叫通信卫星。
3颗同步卫星可实现全球覆盖
为了卫星之间不互相干扰,大约3°左右才能放置1颗,这样地球的同步卫星只能有120颗。可见,空间位置也是一种资源。
3、地球同步卫星是联系地面上的物体与天上的卫星的桥梁
A
B
C
A是地面上的物体
B是同步卫星
C是一般卫星
同轴传动
都是卫星
笔记时间
(单选)“神舟”十号飞船在圆轨道上运转一圈的时间为90分钟,由此他将“神舟”十号飞船与同步卫星进行比较,正确的是(
)
A.“神舟”
十号飞船运行的轨道和同步卫星的轨道是同一轨道
B.“神舟”
十号飞船运行的角速度大于同步卫星的角速度
C.“神舟”
十号飞船运行的向心加速度小于同步卫星的加速度
D.“神舟”
十号飞船在圆轨道上的速率小于同步卫星的速率
B
例2:
关于地球同步卫星,下列说法正确的是(
)
A.它的运行速度小于7.9km/s
B.它的运行速度大于7.9km/s
C.它的周期是24h,且轨道平面于赤道平面重合
D.每一个地球同步卫星离开地面的高度是一样的
ACD
D
1
3
2
V
F引
F引<F向
F引>F向
M
A点速度—内小外大(在A点看轨迹)
在A点万有引力不变,变化的是向心力
A
四、变轨问题
1、
变轨:当卫星点火突然加速或者减速时,由于万有引力不再等于向心力,卫星将做近心运动或者离心运动,卫星将变轨。
①为了节省能量,在赤道上顺着地球自转方向发射卫星到近地圆轨道Ⅰ上。
③在椭圆轨道Ⅱ上的Q
点(远地点),由于万有引力大于向心力,故从Q点开始做近心运动,若再次点火加速可使万有引力等于向心力,使卫星进入圆形轨道Ⅲ做圆周运动。
2、
发射卫星——两次点火加速
②在
轨道Ⅰ上的P
点突然点火加速,由于速度变大,则需要的向心力也变大,故万有引力不足以提供在轨道Ⅰ上做圆周运动的向心力,卫星做离心运动进入椭圆轨道Ⅱ。
Ⅰ
P
Ⅱ
Q
Ⅲ
②卫星在圆形轨道Ⅲ上的Q点突然点火减速,使得万有引力大于向心力,卫星将沿着椭圆轨道Ⅱ做近心运动。
①卫星在圆形轨道Ⅲ做圆周运动。
3、
回收卫星——两次点火减速
③在椭圆轨道Ⅱ上的P
点(远地点),由于万有引力小于向心力,故从P点开始做离心运动,若再次点火减速可使万有引力等于向心力,使卫星进入圆形轨道Ⅰ做圆周运动。
Ⅰ
P
Ⅱ
Q
Ⅲ
4、总结规律
Ⅰ
P
Ⅱ
Q
Ⅲ
①线速度
②周期
③加速度
椭圆:近快远慢
圆:利用
相切点:内小外大
无论是圆还是椭圆都用:
r1
r3
2r2
无论什么位置都用:
注意:不是向心加速度
例题、如图所示,发射同步卫星时,先将卫星发射至近地圆轨道1,然后经点火使其沿椭圆轨道2运行;最后再次点火将其送入同步圆轨道3。轨道1、2相切于P点,2、3相切于Q点。当卫星分别在1、2、3上正常运行时,以下说法正确的是(
)
A、在轨道3上的速率大于1上的速率
B、在轨道3上的角速度小于1上的角速度
C、在轨道2上经过Q点时的速率等于在轨道3
上经过Q点时的速率
D、在轨道1上经过P点时的加速度等于在轨道2
上经过P点时的加速度
Q
P
2
·
3
1
BD
月球
月球轨道
地球
地月转移轨道
点火加速
减速制动
月球探测卫星发射
2.
2007年10月24日“嫦娥一号”卫星星箭分离,卫星进入绕地轨道。在绕地运行时,要经过三次近地变轨:12小时椭圆轨道①→24小时椭圆轨道②→48小时椭圆轨道③→修正轨道④→地月转移轨道⑤。11月5日11时,当卫星经过距月球表面高度为h的A点时,再经三次变轨:12小时椭圆轨道⑥→3.5小时椭圆
轨道⑦→最后进入周期为T的极月圆轨道⑧
,如图所示(
)
A.“嫦娥一号”由⑤到⑥需加速、由⑦到⑧需减速
B.发射“嫦娥一号”的速度必须达到第三宇宙速度
C.在绕月圆轨道上,卫星周期与卫星质量有关
D.卫星受月球的引力与它到月球中心距离的平方成反比
E.在绕月圆轨道上,卫星受地球的引力大于受月球的引力
①
②
③
近地变轨
轨道修正
转移轨道
④
⑤
⑥
⑦
⑧
发射
D
5、交会对接
后下方加速
前上方减速
5、交会对接
再加速
后方先减速变轨
例:在太空中有两飞行器a、b,它们在绕地球的同一圆形轨道上同向运行,a在前b在后,它都配有能沿运动方向向前或向后喷气的发动机,现要想b
尽快追上a
并完成对接,b应采取的措施是(
)
A、沿运动方向喷气
B、先沿运动方向喷气,后沿运动反方向喷气
C、沿运动反方向喷气
D、先沿运动反方向喷气,后沿运动方向喷气
B
新课学习
史上第一人
五、梦想成真—人类航天史
新课学习
理论泰斗
新课学习
女汉子不让须眉
新课学习
彪悍的人生不需要解释
新课学习
杨利伟
翟志刚
刘洋
王亚平
中国航天历程
