人教版高中物理 必修二 第六章 6.4万有引力理论的成就(共21张PPT)
文档属性
| 名称 | 人教版高中物理 必修二 第六章 6.4万有引力理论的成就(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-07-12 09:59:55 | ||
图片预览






文档简介
(共21张PPT)
第六章
万有引力定律
第
4
节:万有引力理论的成就
笔记时间
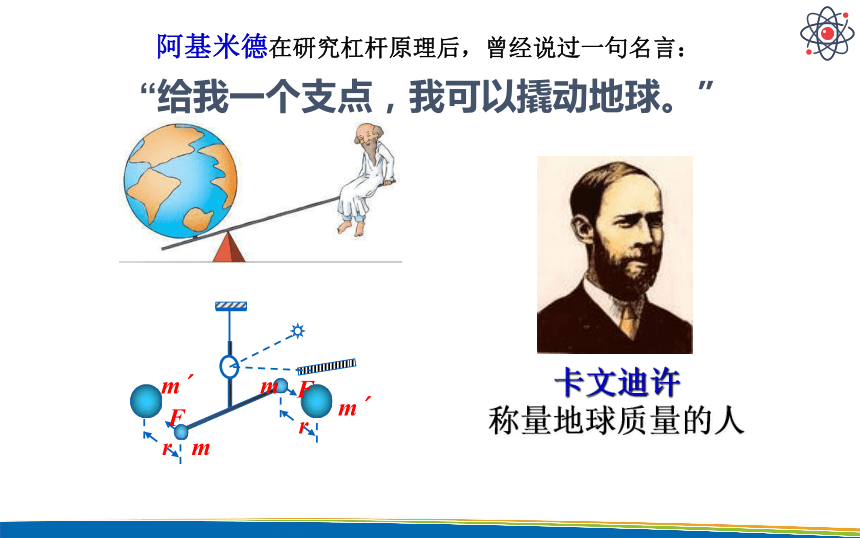
阿基米德在研究杠杆原理后,曾经说过一句名言:
“给我一个支点,我可以撬动地球。”
卡文迪许
称量地球质量的人
r
F
r
F
m
m?
m
m?
G
Fn
F引
R
o
O,
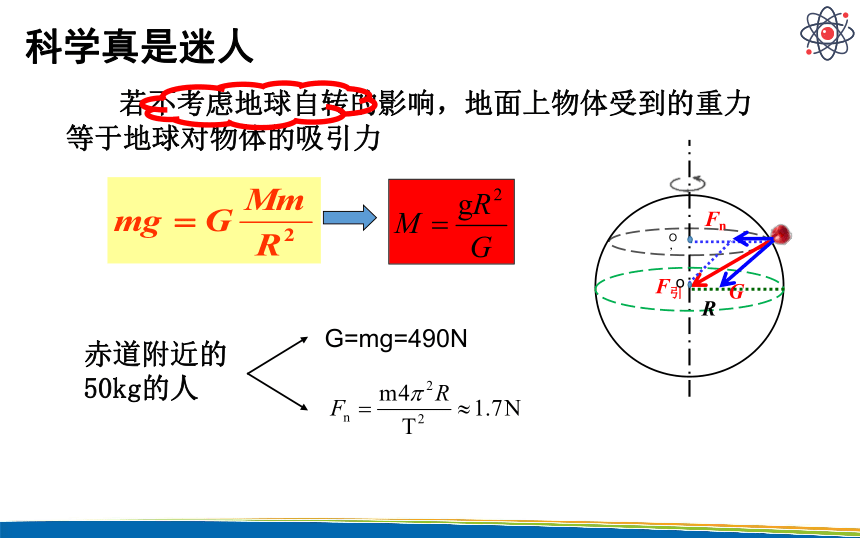
赤道附近的50kg的人
G=mg=490N
若不考虑地球自转的影响,地面上物体受到的重力等于地球对物体的吸引力
科学真是迷人
例1.
设地面附近的重力加速度
g
=
9.8
m/s2,地球半径
R
=
6.4×106
m,引力常量
G
=
6.67×10-11
N?m2/kg2,试估算地球的质量。
解:由
得:
重力加速度
g
和地球半径
R
在卡文迪许之前就知道了,一旦测得引力常量
G,则可以算出地球质量
M。
正是因为如此卡文迪许被称为“称量地球质量的人”。
科学真是迷人
在实验室里测量几个铅球之间的作用力,就可以称量地球,这不能不说是一个科学奇迹。难怪一位外行人、著名文学家马克·吐温满怀激情地说:“科学真是迷人,根据零星的事实,增添一点猜想,就能赢得那么多收获!”
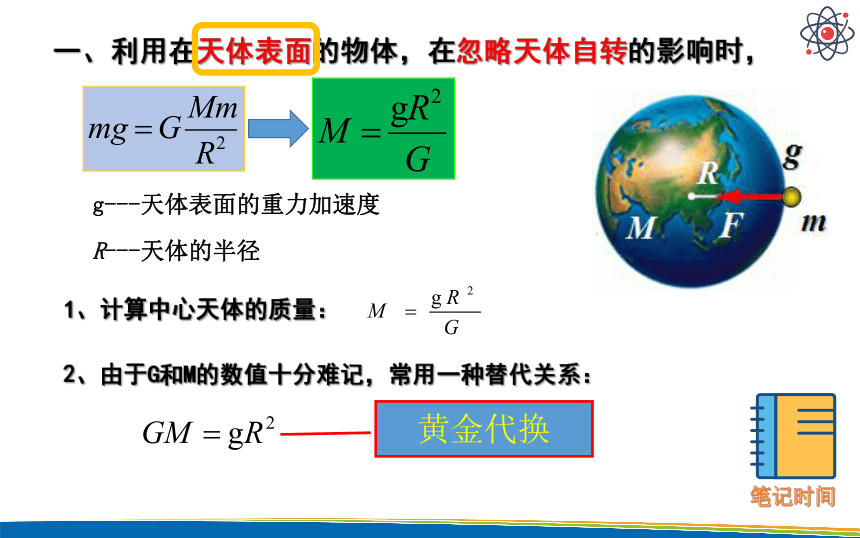
g---天体表面的重力加速度
R---天体的半径
一、利用在天体表面的物体,在忽略天体自转的影响时,
1、计算中心天体的质量:
2、由于G和M的数值十分难记,常用一种替代关系:
黄金代换
笔记时间
例
2.
宇航员站在一个星球表面上的某高处
h
自由释放一小球,经过时间
t
落地,该星球的半径为
R,你能求解出该星球的质量吗?
在星球表面,重力等于万有引力得
解得:
解:释放小球后小球做自由落体运动
故星球质量为
计算地球的质量其他方法
月球绕地球周期T=27.3天,
月地平均距离r=3.84×108m
二、利用在围绕中心天体做圆周运动的环绕天体,由万有引力提供向心力。
笔记时间
M:中心天体的质量
m:环绕天体的质量
R:中心天体的半径
r:圆周运动的轨道半径
M
M
m
m
在中心天体的表面做圆周运动时,r=R
在中心天体的上空做圆周运动时,r=R+h
笔记时间
1、环绕天体的运动规律:
r
v
ω
T
an
笔记时间
2、只能求解中心天体的质量,无法求解环绕天体的质量,也无法求万有引力。
最有价值
笔记时间
3、求解中心天体的平均密度
只能代入中心天体的半径R
若环绕天体在中心天体的表面上做圆周运动,则r=R。代入上式得
可见中心天体的密度只与在天体表面做圆周运动的环绕天体的周期有关。
r=R
笔记时间
4、可见开普勒第三定律中的k值只与中心天体的质量有关。
例3.
把地球绕太阳的公转看作是匀速圆周运动,轨道半径约为
1.5×1011
km,已知引力常量
G
=
6.67×10-11
N·m2/kg2,则可估算出太阳的质量约为
kg。
解:地球绕太阳运转周期:
T
=
365×24×60×60
s
=
3.15×107
s
地球绕太阳做匀速圆周运动的向心力由万有引力提供。
太阳是中心天体,质量是M
地球是环绕天体,质量是m
海王星
发现未知天体
天王星的实际运动的观测与计算出的轨道有偏差,推测在天王星的外侧还有一颗行星。英国的剑桥大学的学生亚当斯和法国年轻的天文爱好者勒维耶各自独立计算出这颗“新”行星。1846
年9
月23日晚,由德国的伽勒在勒维耶预言的位置附近发现了这颗行星,人们称其为“笔尖下发现的行星”。这颗行星就是“海王星”。
法国天文学家勒维耶
英国剑桥大学亚当斯
笔尖下发现的行星还有:哈雷彗星。。。
双星系统
天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星。双星系统在银河系中很普遍,银河系的恒星中大约四分之一是双星。它由两个相互环绕的天体组成,它们在相互之间的万有引力作用下,绕连线上某点做周期相同的匀速圆周运动。
m1
m2
r1
r2
1.双星属于同轴转动,故双星的ω、T、f、n都相等。
三、双星系统
笔记时间
2.双星之间的万有引力提供各自圆周运动的向心力,故双星的向心力也相等。
3.双星的轨道半径与质量成反比,质量大的半径较小。
4.双星的线速度与半径成正比,与质量成反比。
笔记时间
5.双星转动的快慢(例如角速度ω)由双星的质量之和与二者间距决定。
先约掉质量,再等号两边相加
解得
得:
解:双星之间的万有引力提供各自圆周运动的向心力
先约掉质量,再等号两边相加
而R=r1+r2代入得:
课堂小结
THANKS
“
”
第六章
万有引力定律
第
4
节:万有引力理论的成就
笔记时间
阿基米德在研究杠杆原理后,曾经说过一句名言:
“给我一个支点,我可以撬动地球。”
卡文迪许
称量地球质量的人
r
F
r
F
m
m?
m
m?
G
Fn
F引
R
o
O,
赤道附近的50kg的人
G=mg=490N
若不考虑地球自转的影响,地面上物体受到的重力等于地球对物体的吸引力
科学真是迷人
例1.
设地面附近的重力加速度
g
=
9.8
m/s2,地球半径
R
=
6.4×106
m,引力常量
G
=
6.67×10-11
N?m2/kg2,试估算地球的质量。
解:由
得:
重力加速度
g
和地球半径
R
在卡文迪许之前就知道了,一旦测得引力常量
G,则可以算出地球质量
M。
正是因为如此卡文迪许被称为“称量地球质量的人”。
科学真是迷人
在实验室里测量几个铅球之间的作用力,就可以称量地球,这不能不说是一个科学奇迹。难怪一位外行人、著名文学家马克·吐温满怀激情地说:“科学真是迷人,根据零星的事实,增添一点猜想,就能赢得那么多收获!”
g---天体表面的重力加速度
R---天体的半径
一、利用在天体表面的物体,在忽略天体自转的影响时,
1、计算中心天体的质量:
2、由于G和M的数值十分难记,常用一种替代关系:
黄金代换
笔记时间
例
2.
宇航员站在一个星球表面上的某高处
h
自由释放一小球,经过时间
t
落地,该星球的半径为
R,你能求解出该星球的质量吗?
在星球表面,重力等于万有引力得
解得:
解:释放小球后小球做自由落体运动
故星球质量为
计算地球的质量其他方法
月球绕地球周期T=27.3天,
月地平均距离r=3.84×108m
二、利用在围绕中心天体做圆周运动的环绕天体,由万有引力提供向心力。
笔记时间
M:中心天体的质量
m:环绕天体的质量
R:中心天体的半径
r:圆周运动的轨道半径
M
M
m
m
在中心天体的表面做圆周运动时,r=R
在中心天体的上空做圆周运动时,r=R+h
笔记时间
1、环绕天体的运动规律:
r
v
ω
T
an
笔记时间
2、只能求解中心天体的质量,无法求解环绕天体的质量,也无法求万有引力。
最有价值
笔记时间
3、求解中心天体的平均密度
只能代入中心天体的半径R
若环绕天体在中心天体的表面上做圆周运动,则r=R。代入上式得
可见中心天体的密度只与在天体表面做圆周运动的环绕天体的周期有关。
r=R
笔记时间
4、可见开普勒第三定律中的k值只与中心天体的质量有关。
例3.
把地球绕太阳的公转看作是匀速圆周运动,轨道半径约为
1.5×1011
km,已知引力常量
G
=
6.67×10-11
N·m2/kg2,则可估算出太阳的质量约为
kg。
解:地球绕太阳运转周期:
T
=
365×24×60×60
s
=
3.15×107
s
地球绕太阳做匀速圆周运动的向心力由万有引力提供。
太阳是中心天体,质量是M
地球是环绕天体,质量是m
海王星
发现未知天体
天王星的实际运动的观测与计算出的轨道有偏差,推测在天王星的外侧还有一颗行星。英国的剑桥大学的学生亚当斯和法国年轻的天文爱好者勒维耶各自独立计算出这颗“新”行星。1846
年9
月23日晚,由德国的伽勒在勒维耶预言的位置附近发现了这颗行星,人们称其为“笔尖下发现的行星”。这颗行星就是“海王星”。
法国天文学家勒维耶
英国剑桥大学亚当斯
笔尖下发现的行星还有:哈雷彗星。。。
双星系统
天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星。双星系统在银河系中很普遍,银河系的恒星中大约四分之一是双星。它由两个相互环绕的天体组成,它们在相互之间的万有引力作用下,绕连线上某点做周期相同的匀速圆周运动。
m1
m2
r1
r2
1.双星属于同轴转动,故双星的ω、T、f、n都相等。
三、双星系统
笔记时间
2.双星之间的万有引力提供各自圆周运动的向心力,故双星的向心力也相等。
3.双星的轨道半径与质量成反比,质量大的半径较小。
4.双星的线速度与半径成正比,与质量成反比。
笔记时间
5.双星转动的快慢(例如角速度ω)由双星的质量之和与二者间距决定。
先约掉质量,再等号两边相加
解得
得:
解:双星之间的万有引力提供各自圆周运动的向心力
先约掉质量,再等号两边相加
而R=r1+r2代入得:
课堂小结
THANKS
“
”
