三年级下册数学课件-7.8 整理与提高 数学广场(放苹果)沪教版 (共27张PPT)
文档属性
| 名称 | 三年级下册数学课件-7.8 整理与提高 数学广场(放苹果)沪教版 (共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-11 00:00:00 | ||
图片预览







文档简介
游戏要求:
从一副扑克牌(除去大小王)中,5人每人随意抽一张。
“魔术”天地
操作要求:
〈1〉小组4人合作,组员负责摆放3个小圆片,组长将相应的数据记录在表格中,轮流摆放。
〈2〉做到不遗漏、不重复。
3个苹果放入2个抽屉
探究一
抽屉一
抽屉二
抽屉一
抽屉二
抽屉一
抽屉二
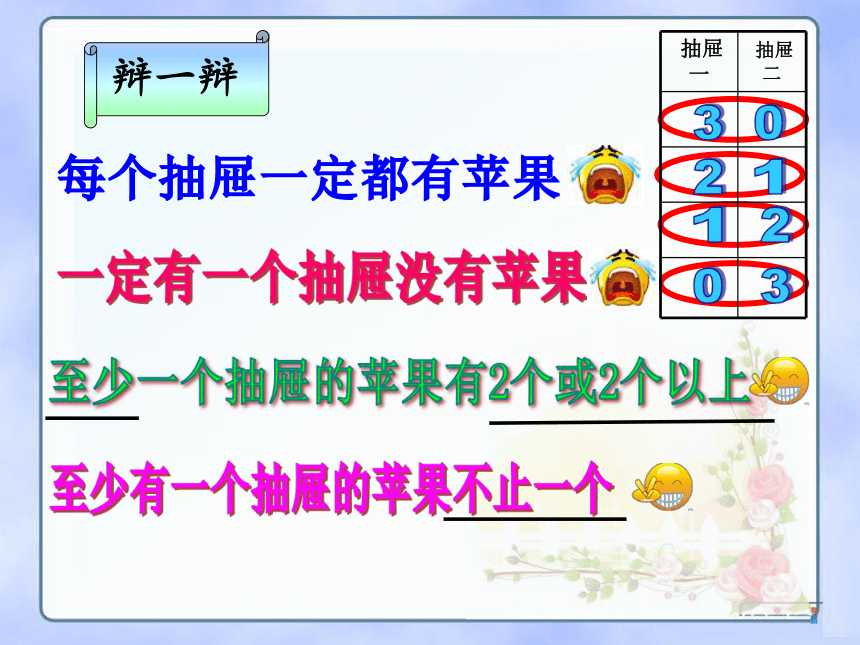
辩一辩
发现:3个苹果放入2个抽屉,
抽屉1
抽屉2
至少有一个抽屉的苹果不止一个。
是不是所有苹果数比抽屉数多1的情况都有这样的结论呢?
4个苹果放入3个抽屉
要求:
〈1〉小组4人一组,利用2分钟时间,尽可能多的写出摆放的方法。
〈2〉可以借助小圆片操作。
〈3〉有序、规律思考,做到不遗漏、不重复。
探究二
抽屉一
抽屉二
抽屉三
0
0
4
0
1
3
0
2
2
0
3
1
0
4
0
1
0
3
1
1
2
1
2
1
1
3
0
2
0
2
2
1
1
2
2
0
3
0
1
3
1
0
4
0
0
04
13
22
31
40
03
12
21
30
02
11
20
01
00
10
推测:5个苹果放入4个抽屉会有怎样的结论呢?
5个苹果放入4个抽屉,至少有一个抽屉里的苹果不止一个。
亲爱的同学们,从放苹果的挑战任务中,你有什么收获吗?
放的苹果数比抽屉数_____,不管怎么放,_____有一个抽屉的苹果 _ _。
多1
至少
不止一个
任意抽取一副除大小王之外扑克牌中的5张牌,至少有( )张是同花色的。
“魔术”天地
2
4种花色
----- 4个抽屉
5张牌
----- 5个苹果
抽屉原理
“ 抽屉原理”又称“鸽笼原理”,最先是由19世纪的德国数学家狄利克雷提出来的。这一原理在解决实际问题中有着广泛的应用。“抽屉原理”的应用是千变万化的,用它可以解决许多有趣的问题。
三个
性别
小朋友
判断题:3个小朋友同行,其中必有2个小朋友性别相同 ( )
√
1
判断题:从电影院中任意找来13个观众,可能每个人的生肖是不相同。( )
13个
12生肖
12个抽屉
13个苹果
观众
X
1
用红、黄、蓝、绿、黑5种颜色给正方体的各面涂色(每面只涂一种颜色),至少有几个面涂色相同?
2
一副扑克牌,去掉大小王,还剩52张。
至少取出( )张,一定有相同点数的牌出现。
14
------- 13个
3
你们太棒了!
拓展活动
游戏要求:
〈1〉假设每个小朋友就是1个苹果,每把椅子就是1个抽屉。
〈2〉听到音乐响起围着椅子绕圈,音乐结束每个小朋友要坐在椅子上。
〈3〉可以1把椅子坐几个小朋友。
拓展活动
那苹果数比抽屉数多3、4、5……的情况会不会有这样的结论呢?
课后活动
放的苹果数比抽屉数_______,不管怎么放,_____有一个抽屉的苹果 _ _。
多1
至少
不止一个
至少
从一副扑克牌(除去大小王)中,5人每人随意抽一张。
“魔术”天地
操作要求:
〈1〉小组4人合作,组员负责摆放3个小圆片,组长将相应的数据记录在表格中,轮流摆放。
〈2〉做到不遗漏、不重复。
3个苹果放入2个抽屉
探究一
抽屉一
抽屉二
抽屉一
抽屉二
抽屉一
抽屉二
辩一辩
发现:3个苹果放入2个抽屉,
抽屉1
抽屉2
至少有一个抽屉的苹果不止一个。
是不是所有苹果数比抽屉数多1的情况都有这样的结论呢?
4个苹果放入3个抽屉
要求:
〈1〉小组4人一组,利用2分钟时间,尽可能多的写出摆放的方法。
〈2〉可以借助小圆片操作。
〈3〉有序、规律思考,做到不遗漏、不重复。
探究二
抽屉一
抽屉二
抽屉三
0
0
4
0
1
3
0
2
2
0
3
1
0
4
0
1
0
3
1
1
2
1
2
1
1
3
0
2
0
2
2
1
1
2
2
0
3
0
1
3
1
0
4
0
0
04
13
22
31
40
03
12
21
30
02
11
20
01
00
10
推测:5个苹果放入4个抽屉会有怎样的结论呢?
5个苹果放入4个抽屉,至少有一个抽屉里的苹果不止一个。
亲爱的同学们,从放苹果的挑战任务中,你有什么收获吗?
放的苹果数比抽屉数_____,不管怎么放,_____有一个抽屉的苹果 _ _。
多1
至少
不止一个
任意抽取一副除大小王之外扑克牌中的5张牌,至少有( )张是同花色的。
“魔术”天地
2
4种花色
----- 4个抽屉
5张牌
----- 5个苹果
抽屉原理
“ 抽屉原理”又称“鸽笼原理”,最先是由19世纪的德国数学家狄利克雷提出来的。这一原理在解决实际问题中有着广泛的应用。“抽屉原理”的应用是千变万化的,用它可以解决许多有趣的问题。
三个
性别
小朋友
判断题:3个小朋友同行,其中必有2个小朋友性别相同 ( )
√
1
判断题:从电影院中任意找来13个观众,可能每个人的生肖是不相同。( )
13个
12生肖
12个抽屉
13个苹果
观众
X
1
用红、黄、蓝、绿、黑5种颜色给正方体的各面涂色(每面只涂一种颜色),至少有几个面涂色相同?
2
一副扑克牌,去掉大小王,还剩52张。
至少取出( )张,一定有相同点数的牌出现。
14
------- 13个
3
你们太棒了!
拓展活动
游戏要求:
〈1〉假设每个小朋友就是1个苹果,每把椅子就是1个抽屉。
〈2〉听到音乐响起围着椅子绕圈,音乐结束每个小朋友要坐在椅子上。
〈3〉可以1把椅子坐几个小朋友。
拓展活动
那苹果数比抽屉数多3、4、5……的情况会不会有这样的结论呢?
课后活动
放的苹果数比抽屉数_______,不管怎么放,_____有一个抽屉的苹果 _ _。
多1
至少
不止一个
至少
