苏科版七年级下册数学课件: 7.2探索平行线的性质(22张)
文档属性
| 名称 | 苏科版七年级下册数学课件: 7.2探索平行线的性质(22张) |  | |
| 格式 | ppt | ||
| 文件大小 | 964.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-13 11:41:51 | ||
图片预览


文档简介
7.2 探索平行线的性质
? 图片欣赏
复习回顾
平行线的判定方法是什么?
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
同位角相等
内错角相等
同旁内角互补
两直线平行
A
B
C
D
E
F
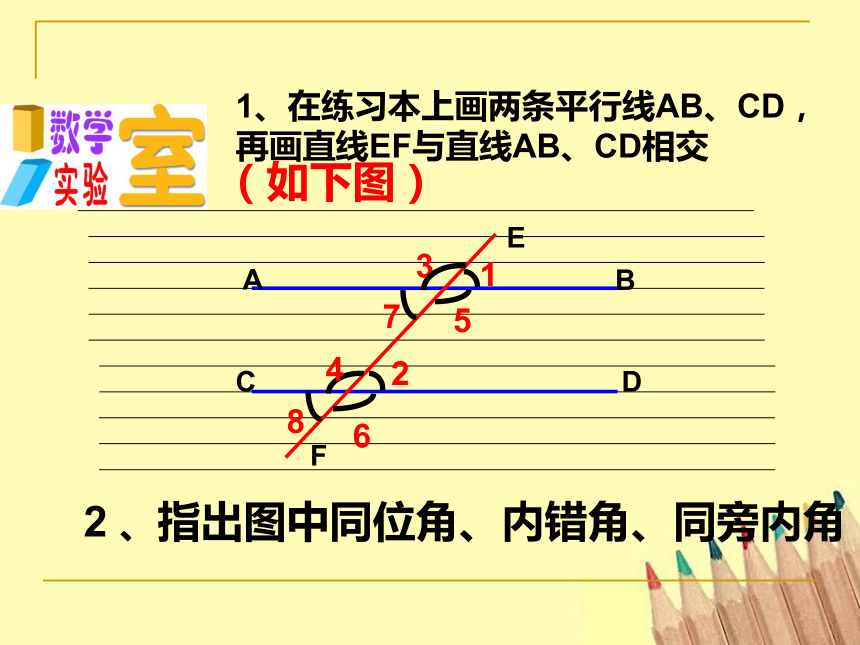
1、在练习本上画两条平行线AB、CD,再画直线EF与直线AB、CD相交
2 、指出图中同位角、内错角、同旁内角
1
3
6
8
2
5
7
4
(如下图)
A
B
C
D
E
F
1
3
6
8
2
5
7
4
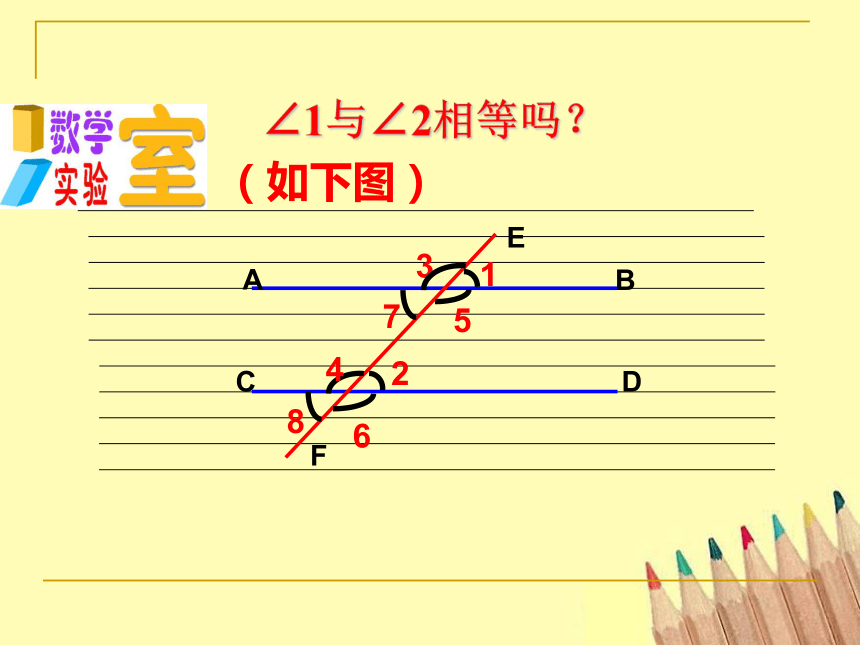
(如下图)
∠1与∠2相等吗?
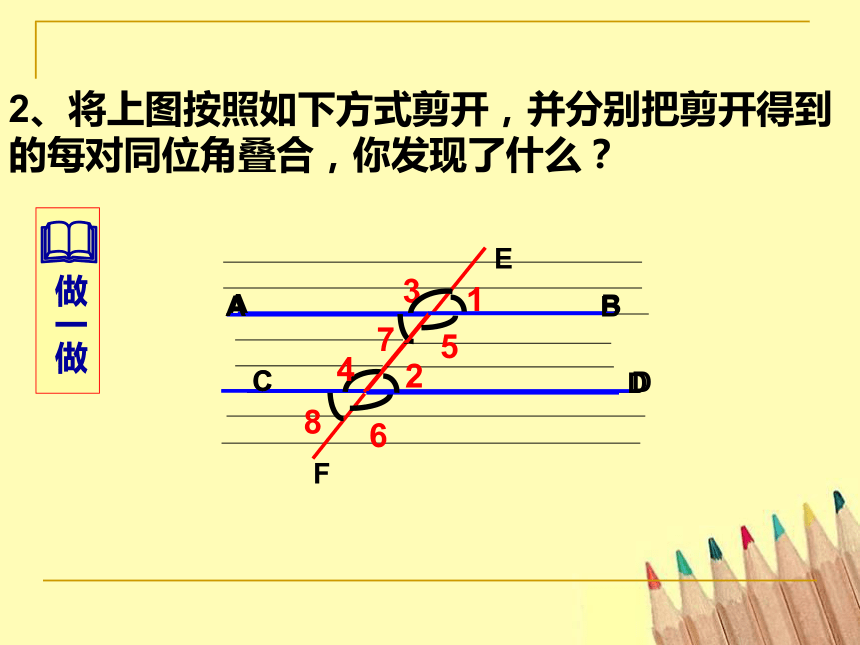
2、将上图按照如下方式剪开,并分别把剪开得到的每对同位角叠合,你发现了什么?
A
B
E
3
1
C
D
F
8
6
A
C
7
4
B
D
5
2
?
做一做
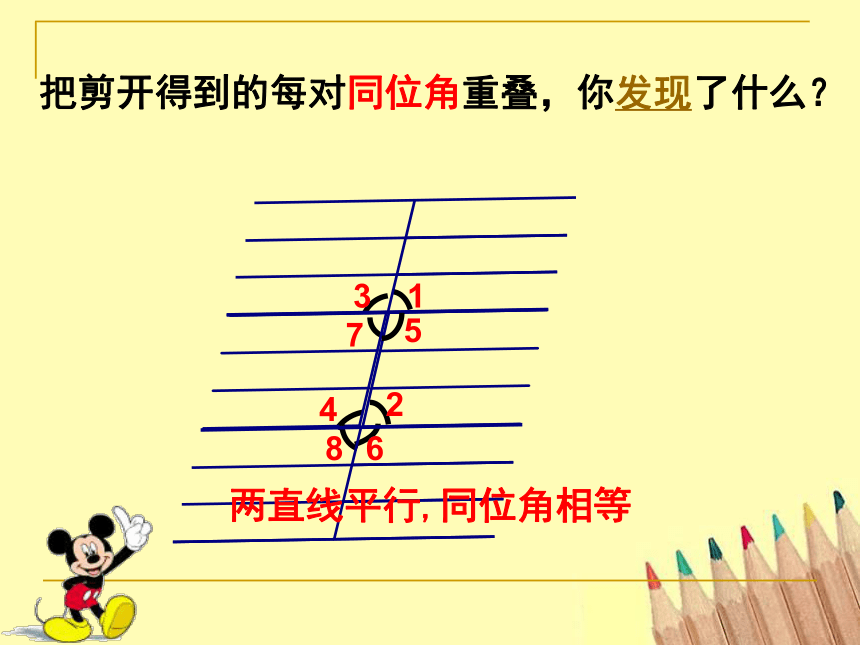
把剪开得到的每对同位角重叠,你发现了什么?
3
1
7
4
5
2
8
6
两直线平行,同位角相等
两直线平行,同位角相等.
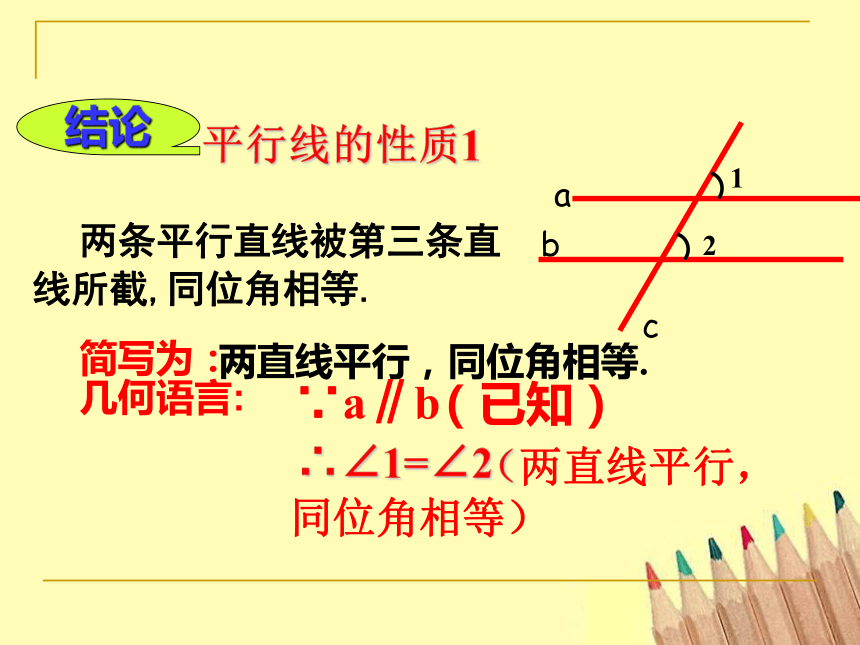
平行线的性质1
结论
两条平行直线被第三条直
线所截,同位角相等.
∴∠1=∠2
∵a∥b
简写为:
几何语言:
b
1
2
a
c
(已知)
(两直线平行,同位角相等)
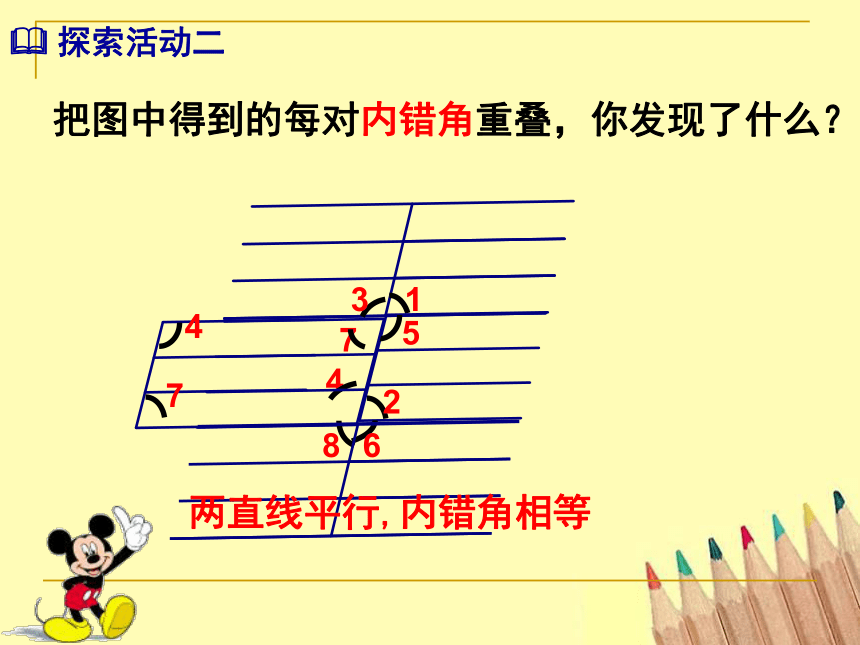
把图中得到的每对内错角重叠,你发现了什么?
3
1
5
2
7
4
8
6
两直线平行,内错角相等
? 探索活动二
4
7
将图中的每对同旁内角剪成两部分,并把他们拼到一起去,你发现每对同旁内角之间有什么关系?
3
1
5
2
7
4
8
6
两直线平行,同旁内角互补
? 探索活动三
7
4
你能根据“两直线平行,同位角相等”,说明“两直线平行,内错角相等”成立的理由吗?
a
b
c
1
2
3
解:如图所示
∵ a∥b
∴∠1=∠2(两直线平行,同位角相等)
又 ∵∠1=∠3
∴∠2=∠3 (等量代换)
? 做一做
两直线平行,内错角相等.
平行线的性质2
结论
两条平行直线被第三条直
线所截,内错角相等.
∴∠1=∠2
∵a∥b
几何语言:
简写为:
b
1
2
a
c
(两直线平行, 内错角相等)
(已知)
如果我们现在只知道“两直线平行,同位角相等”,你能说明“两直线平行,同旁内角互补”成立的理由吗?
解:如图所示
∵ a∥b
∴∠1=∠2
(两直线平行,同位角相等)
又∵∠1+∠3=180°
∴∠2+∠3=180
(等量代换)
? 做一做
1
a
3
2
b
两直线平行,同旁内角互补.
平行线的性质3
结论
两条平行直线被第三条直
线所截,同旁内角互补.
∴? 1+ ? 2=180°
∵a∥b
几何语言:
简写为:
b
1
2
a
c
(已知)
(两直线平行,同旁内角互补)
平行线的性质
(1)两直线平行,同位角相等
几何语言:∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
(2)两直线平行,内错角相等
几何语言:∵a∥b(已知)
∴∠1=∠2(两直线平行,内错角相等)
(3)两直线平行,同旁内角互补
几何语言:∵a∥b(已知)
∴∠1+∠2=180°(两直线平行,同旁内角互补)
b
1
2
a
c
b
1
2
a
c
b
1
2
a
c
及时巩固:
已知:AB//CD,AB和CD被直线BE所截,若∠4=60°,
则∠1=______=______°( )
A
B
C
D
E
4
3
2
1
∠2=______=______°( )
∠3+______=______ °( )
则∠3=____ °
例1、如图AB∥CD,∠A=∠D,试说明AF∥ED
A
F
E
D
B
C
②如图,AB∥CD,AF∥ED,试说明∠A=∠D
①如图,∠A=∠D,AF∥ED,试说明AB∥CD
练习1:如图 ∥ , ⊥ , 与 有怎样的位置
关系?
1
2
如图;①l1//l2,②l3⊥l1③l3 ⊥ l2, 你选择______和______为条件,_____为结论。
你的结论是否成立,请说明理由。
练习2、如图,CD//EF,DE//AC,请找出图中相等的角,并说明理由。
A
B
E
C
D
F
练习3:如图,点B、C、D在一条直线上,AB∥CE,∠A=55°,∠B=60°.求∠1、∠2和∠ACB的度数.
D
C
E
F
A
A
G
G
1
2
小明在纸上画了一个角∠A,准备用量角器测量它的度数时,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC、FE的话,你能帮他设计出多少种方法可以测出∠A的度数?
? 挑战无处不在
? 图片欣赏
复习回顾
平行线的判定方法是什么?
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
同位角相等
内错角相等
同旁内角互补
两直线平行
A
B
C
D
E
F
1、在练习本上画两条平行线AB、CD,再画直线EF与直线AB、CD相交
2 、指出图中同位角、内错角、同旁内角
1
3
6
8
2
5
7
4
(如下图)
A
B
C
D
E
F
1
3
6
8
2
5
7
4
(如下图)
∠1与∠2相等吗?
2、将上图按照如下方式剪开,并分别把剪开得到的每对同位角叠合,你发现了什么?
A
B
E
3
1
C
D
F
8
6
A
C
7
4
B
D
5
2
?
做一做
把剪开得到的每对同位角重叠,你发现了什么?
3
1
7
4
5
2
8
6
两直线平行,同位角相等
两直线平行,同位角相等.
平行线的性质1
结论
两条平行直线被第三条直
线所截,同位角相等.
∴∠1=∠2
∵a∥b
简写为:
几何语言:
b
1
2
a
c
(已知)
(两直线平行,同位角相等)
把图中得到的每对内错角重叠,你发现了什么?
3
1
5
2
7
4
8
6
两直线平行,内错角相等
? 探索活动二
4
7
将图中的每对同旁内角剪成两部分,并把他们拼到一起去,你发现每对同旁内角之间有什么关系?
3
1
5
2
7
4
8
6
两直线平行,同旁内角互补
? 探索活动三
7
4
你能根据“两直线平行,同位角相等”,说明“两直线平行,内错角相等”成立的理由吗?
a
b
c
1
2
3
解:如图所示
∵ a∥b
∴∠1=∠2(两直线平行,同位角相等)
又 ∵∠1=∠3
∴∠2=∠3 (等量代换)
? 做一做
两直线平行,内错角相等.
平行线的性质2
结论
两条平行直线被第三条直
线所截,内错角相等.
∴∠1=∠2
∵a∥b
几何语言:
简写为:
b
1
2
a
c
(两直线平行, 内错角相等)
(已知)
如果我们现在只知道“两直线平行,同位角相等”,你能说明“两直线平行,同旁内角互补”成立的理由吗?
解:如图所示
∵ a∥b
∴∠1=∠2
(两直线平行,同位角相等)
又∵∠1+∠3=180°
∴∠2+∠3=180
(等量代换)
? 做一做
1
a
3
2
b
两直线平行,同旁内角互补.
平行线的性质3
结论
两条平行直线被第三条直
线所截,同旁内角互补.
∴? 1+ ? 2=180°
∵a∥b
几何语言:
简写为:
b
1
2
a
c
(已知)
(两直线平行,同旁内角互补)
平行线的性质
(1)两直线平行,同位角相等
几何语言:∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
(2)两直线平行,内错角相等
几何语言:∵a∥b(已知)
∴∠1=∠2(两直线平行,内错角相等)
(3)两直线平行,同旁内角互补
几何语言:∵a∥b(已知)
∴∠1+∠2=180°(两直线平行,同旁内角互补)
b
1
2
a
c
b
1
2
a
c
b
1
2
a
c
及时巩固:
已知:AB//CD,AB和CD被直线BE所截,若∠4=60°,
则∠1=______=______°( )
A
B
C
D
E
4
3
2
1
∠2=______=______°( )
∠3+______=______ °( )
则∠3=____ °
例1、如图AB∥CD,∠A=∠D,试说明AF∥ED
A
F
E
D
B
C
②如图,AB∥CD,AF∥ED,试说明∠A=∠D
①如图,∠A=∠D,AF∥ED,试说明AB∥CD
练习1:如图 ∥ , ⊥ , 与 有怎样的位置
关系?
1
2
如图;①l1//l2,②l3⊥l1③l3 ⊥ l2, 你选择______和______为条件,_____为结论。
你的结论是否成立,请说明理由。
练习2、如图,CD//EF,DE//AC,请找出图中相等的角,并说明理由。
A
B
E
C
D
F
练习3:如图,点B、C、D在一条直线上,AB∥CE,∠A=55°,∠B=60°.求∠1、∠2和∠ACB的度数.
D
C
E
F
A
A
G
G
1
2
小明在纸上画了一个角∠A,准备用量角器测量它的度数时,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC、FE的话,你能帮他设计出多少种方法可以测出∠A的度数?
? 挑战无处不在
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
