苏科版七年级下册数学课件 7.5 多边形的内角和与外角和(19张)
文档属性
| 名称 | 苏科版七年级下册数学课件 7.5 多边形的内角和与外角和(19张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 519.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-13 00:00:00 | ||
图片预览




文档简介
7.5 多边形的内角和
与外角和(1)
苏科版 数学 七年级下册
A
B
C
请同学们画△ABC,把△ABC的3个内角剪开(如左图),然后把它们的顶点A、B、C重合在同一点,拼成右图.
通过以上操作,你得到了什么结论?
三角形三个内角的和等于180°.
与
结论:
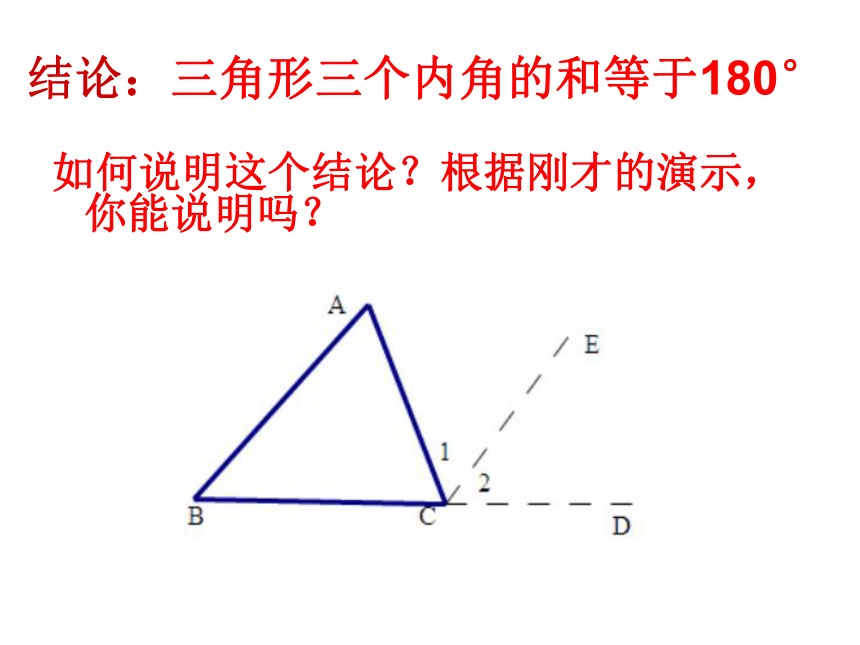
结论:三角形三个内角的和等于180°
如何说明这个结论?根据刚才的演示,你能说明吗?
议一议
1
2
a
b
A
B
如图,3根木条相交得∠1、∠2.若a∥b,则∠1+∠2= .理由: .
两直线平行,同旁内角互补
180°
结论:
三角形三个内角的和等于180°.
C
把木条a绕点A转动,使它与木条b相交于点C.
根据图形,你能说明上述结论吗?
(
3
(
4
(
5
a
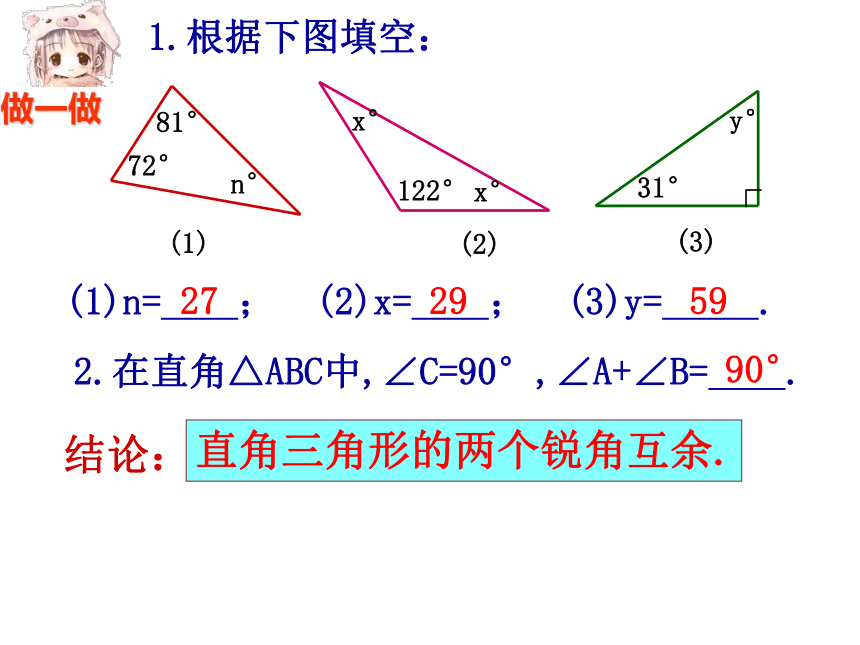
1.根据下图填空:
(1)n= ; (2)x= ; (3)y= .
81°
72°
n°
(1)
x°
x°
(2)
∟
31°
y°
(3)
122°
27
29
59
做一做
2.在直角△ABC中,∠C=90°,∠A+∠B= .
90°
结论:
直角三角形的两个锐角互余.
看一看
A
B
C
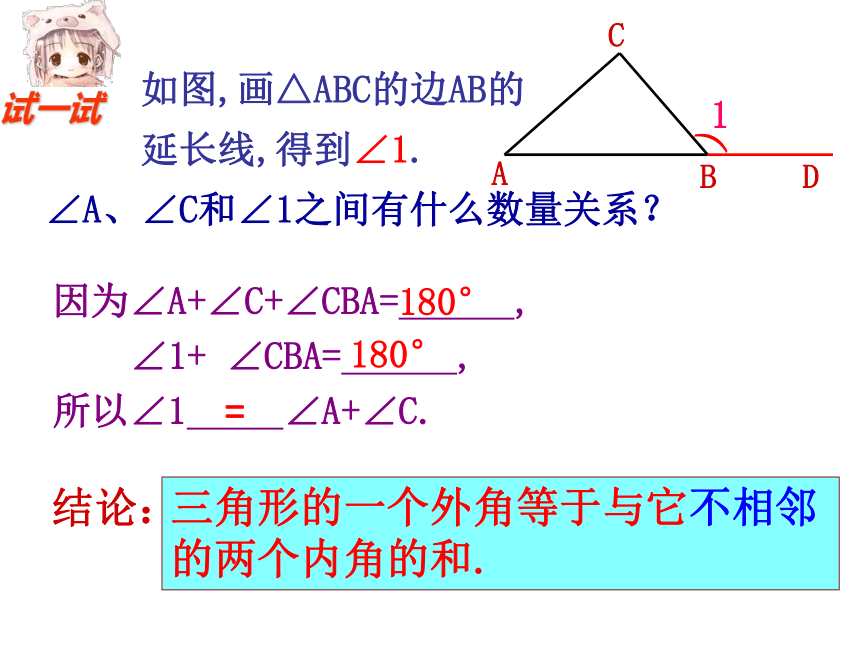
如图,画△ABC的边AB的
延长线,得到∠1.
D
)
1
∠1称为△ABC的一个外角.
三角形的一边与另一边的延长线所组成的角,叫做三角形的 外角 .
C
K
A
D
B
F
E
找找看
图中哪些角是△ABC的外角?
)
A
B
C
如图,画△ABC的边AB的
延长线,得到∠1.
D
)
1
试一试
∠A、∠C和∠1之间有什么数量关系?
因为∠A+∠C+∠CBA= ,
∠1+ ∠CBA= ,
所以∠1 ∠A+∠C.
结论:
三角形的一个外角等于与它不相邻的两个内角的和.
180°
180°
=
找一找:(看谁细心)
(1)如图,D是△ABC内一点,延长CD交AB于E点, ∠ 1 是△ 的外 角; ∠ 2是△ 的外角.
2
A
E
B
C
1
D
(2)如图AC、BD相交于点O, ∠AOD是△ 的外角。
B
A
O
C
D
(3)如图, 是△ABC的外角。
A
B
C
F
D
E
BED
ACE
AOB、 △COD
∠ ACD、 ∠ BCF
1.求图中x和y的值.
x=47
x=50 , y=140
练 一 练
∟
C
x°
y°
(x-10)°
A
B
E
(2)
A
B
C
D
x°
65°
112°
(1)
如图,AC、BD相交于点O,
∠A+∠B=∠C+∠D吗?为什么?
B
A
O
C
D
(
(
1
2
例题评析
(2)直角三角形的外角可能是锐角吗?
为什么?
练 一 练
2.(1)一个三角形的3个内角中,
最多有几个直角?钝角呢?为什么?
练 一 练
3.如图, AD是三角形的角平分线,E是BC延长线上一点,∠3=∠B. 问∠4与∠DAE相等吗?为什么?
A
B
D
C
E
1
2
4
3
(
(
(
(
(
如图,AB//CD,∠ABD与∠BDC的平分线相交于点E,求∠E的度数.
想 一想
E
C
D
A
B
1
2
如图,AB//CD,∠ABD与∠BDC的平分线相交于点E,求∠E的度数.
想 一想
E
C
D
A
B
2
1
解:
因为AB//CD,
所以∠ABD+∠BDC=180°
因为BE平分∠ABD,DE平分∠BDC,
所以∠1= ∠ABD ,
∠2= ∠BDC,
所以∠1+ ∠2= ∠ABD+ ∠BDC
= ( ∠ABD +∠BDC )= ×180°= 90°
在△BED中, ∠1+ ∠2+∠E=180°
所以∠E= 180°- (∠1+ ∠2)= 180°-90°=90°.
(两直线平行,同旁内角互补)
(角平分线的定义)
(三角形的内角和等于180?)
4、如图(1)中是一个五角星,你会求∠A+ ∠B+ ∠C+ ∠D+ ∠E的值吗?
(2)图中的点A向下移到BE上时,五个角的和(即∠CAD+ ∠B+ ∠C+ ∠D+ ∠E )有无变化?如图(2)说明你的结论的正确性。
(3)把图(2)中的点C向上移动到BD上时,五个角的和( 即∠CAD+ ∠B+ ∠ACE+ ∠D+ ∠E )有无变化?如图(3)说明你的结论的正确性。
B
A
E
C
D
A
B
E
C
D
A
B
C
D
E
F
G
5、如图,AD、AE分别是△ABC的角平分线和高,若∠B = 46°, ∠C = 54 °,求出∠CAE 、∠ADE 、∠DAE的度数
E
C
A
B
D
解(1)因为AE是高,所以△AEC是直角三角形。
在直角三角形AEC中,∠CAE+∠C=90°
所以 ∠CAE=90°-∠C=90° -54 °=36 °
(2)在△ABC中,∠B+ ∠C+ ∠BAC=180 °
所以∠BAC= 180 ° - ∠B - ∠C= 180 ° - 46 ° - 54 °= 80 °
因为AD是 △ABC的角平分线,
所以∠BAD= ∠BAC= × 80 °=40°
又因为∠ADE是△ABD的一个外角
所以∠ADE= ∠B+ ∠BAD = 46 ° + 40°= 86 °
(3)在直角三角形ADE中, ∠ADE+ ∠DAE= 90°
所以 ∠DAE= 90° - ∠ADE = 90° - 86 ° = 4°
(直角三角形两锐角互余)
(直角三角形两锐角互余)
(三角形的内角和等于180 °)
(三角形的一个外角等于与它不相邻的两个内角的和)
(角平分线的定义)
5、如图,AD、AE分别是△ABC的角平分线和高,若∠B = 46°, ∠C = 54 °,求出∠CAE 、∠ADE 、∠DAE的度数
E
C
A
B
D
解(1)因为AE是高,所以△AEC是直角三角形。
在直角三角形AEC中,∠CAE+∠C=90°
所以 ∠CAE=90°-∠C=90° -54 °=36 °
(2)在△ABC中,∠B+ ∠C+ ∠BAC=180 °
所以∠BAC= 180 ° - ∠B - ∠C= 180 ° - 46 ° - 54 °= 80 °
因为AD是 △ABC的角平分线,
所以∠BAD= ∠BAC= × 80 °=40°
又因为∠ADE是△ABD的一个外角
所以∠ADE= ∠B+ ∠BAD = 46 ° + 40°= 86 °
(3)在直角三角形ADE中, ∠ADE+ ∠DAE= 90°
所以 ∠DAE= 90° - ∠ADE = 90° - 86 ° = 4°
(直角三角形两锐角互余)
(直角三角形两锐角互余)
(三角形的内角和等于180 °)
(三角形的一个外角等于与它不相邻的两个内角的和)
(角平分线的定义)
课 堂 小 结
(1)重点探究了三角形3个内角之间的
关系以及三角形外角的性质.
三角形3个内角的和等于180°.
三角形的一个外角等于与它不相邻的两个内角的和.
(2)由三角形3个内角之间的关系得到直
角三角形的一个性质:
直角三角形的两个锐角互余.
谢谢观看
与外角和(1)
苏科版 数学 七年级下册
A
B
C
请同学们画△ABC,把△ABC的3个内角剪开(如左图),然后把它们的顶点A、B、C重合在同一点,拼成右图.
通过以上操作,你得到了什么结论?
三角形三个内角的和等于180°.
与
结论:
结论:三角形三个内角的和等于180°
如何说明这个结论?根据刚才的演示,你能说明吗?
议一议
1
2
a
b
A
B
如图,3根木条相交得∠1、∠2.若a∥b,则∠1+∠2= .理由: .
两直线平行,同旁内角互补
180°
结论:
三角形三个内角的和等于180°.
C
把木条a绕点A转动,使它与木条b相交于点C.
根据图形,你能说明上述结论吗?
(
3
(
4
(
5
a
1.根据下图填空:
(1)n= ; (2)x= ; (3)y= .
81°
72°
n°
(1)
x°
x°
(2)
∟
31°
y°
(3)
122°
27
29
59
做一做
2.在直角△ABC中,∠C=90°,∠A+∠B= .
90°
结论:
直角三角形的两个锐角互余.
看一看
A
B
C
如图,画△ABC的边AB的
延长线,得到∠1.
D
)
1
∠1称为△ABC的一个外角.
三角形的一边与另一边的延长线所组成的角,叫做三角形的 外角 .
C
K
A
D
B
F
E
找找看
图中哪些角是△ABC的外角?
)
A
B
C
如图,画△ABC的边AB的
延长线,得到∠1.
D
)
1
试一试
∠A、∠C和∠1之间有什么数量关系?
因为∠A+∠C+∠CBA= ,
∠1+ ∠CBA= ,
所以∠1 ∠A+∠C.
结论:
三角形的一个外角等于与它不相邻的两个内角的和.
180°
180°
=
找一找:(看谁细心)
(1)如图,D是△ABC内一点,延长CD交AB于E点, ∠ 1 是△ 的外 角; ∠ 2是△ 的外角.
2
A
E
B
C
1
D
(2)如图AC、BD相交于点O, ∠AOD是△ 的外角。
B
A
O
C
D
(3)如图, 是△ABC的外角。
A
B
C
F
D
E
BED
ACE
AOB、 △COD
∠ ACD、 ∠ BCF
1.求图中x和y的值.
x=47
x=50 , y=140
练 一 练
∟
C
x°
y°
(x-10)°
A
B
E
(2)
A
B
C
D
x°
65°
112°
(1)
如图,AC、BD相交于点O,
∠A+∠B=∠C+∠D吗?为什么?
B
A
O
C
D
(
(
1
2
例题评析
(2)直角三角形的外角可能是锐角吗?
为什么?
练 一 练
2.(1)一个三角形的3个内角中,
最多有几个直角?钝角呢?为什么?
练 一 练
3.如图, AD是三角形的角平分线,E是BC延长线上一点,∠3=∠B. 问∠4与∠DAE相等吗?为什么?
A
B
D
C
E
1
2
4
3
(
(
(
(
(
如图,AB//CD,∠ABD与∠BDC的平分线相交于点E,求∠E的度数.
想 一想
E
C
D
A
B
1
2
如图,AB//CD,∠ABD与∠BDC的平分线相交于点E,求∠E的度数.
想 一想
E
C
D
A
B
2
1
解:
因为AB//CD,
所以∠ABD+∠BDC=180°
因为BE平分∠ABD,DE平分∠BDC,
所以∠1= ∠ABD ,
∠2= ∠BDC,
所以∠1+ ∠2= ∠ABD+ ∠BDC
= ( ∠ABD +∠BDC )= ×180°= 90°
在△BED中, ∠1+ ∠2+∠E=180°
所以∠E= 180°- (∠1+ ∠2)= 180°-90°=90°.
(两直线平行,同旁内角互补)
(角平分线的定义)
(三角形的内角和等于180?)
4、如图(1)中是一个五角星,你会求∠A+ ∠B+ ∠C+ ∠D+ ∠E的值吗?
(2)图中的点A向下移到BE上时,五个角的和(即∠CAD+ ∠B+ ∠C+ ∠D+ ∠E )有无变化?如图(2)说明你的结论的正确性。
(3)把图(2)中的点C向上移动到BD上时,五个角的和( 即∠CAD+ ∠B+ ∠ACE+ ∠D+ ∠E )有无变化?如图(3)说明你的结论的正确性。
B
A
E
C
D
A
B
E
C
D
A
B
C
D
E
F
G
5、如图,AD、AE分别是△ABC的角平分线和高,若∠B = 46°, ∠C = 54 °,求出∠CAE 、∠ADE 、∠DAE的度数
E
C
A
B
D
解(1)因为AE是高,所以△AEC是直角三角形。
在直角三角形AEC中,∠CAE+∠C=90°
所以 ∠CAE=90°-∠C=90° -54 °=36 °
(2)在△ABC中,∠B+ ∠C+ ∠BAC=180 °
所以∠BAC= 180 ° - ∠B - ∠C= 180 ° - 46 ° - 54 °= 80 °
因为AD是 △ABC的角平分线,
所以∠BAD= ∠BAC= × 80 °=40°
又因为∠ADE是△ABD的一个外角
所以∠ADE= ∠B+ ∠BAD = 46 ° + 40°= 86 °
(3)在直角三角形ADE中, ∠ADE+ ∠DAE= 90°
所以 ∠DAE= 90° - ∠ADE = 90° - 86 ° = 4°
(直角三角形两锐角互余)
(直角三角形两锐角互余)
(三角形的内角和等于180 °)
(三角形的一个外角等于与它不相邻的两个内角的和)
(角平分线的定义)
5、如图,AD、AE分别是△ABC的角平分线和高,若∠B = 46°, ∠C = 54 °,求出∠CAE 、∠ADE 、∠DAE的度数
E
C
A
B
D
解(1)因为AE是高,所以△AEC是直角三角形。
在直角三角形AEC中,∠CAE+∠C=90°
所以 ∠CAE=90°-∠C=90° -54 °=36 °
(2)在△ABC中,∠B+ ∠C+ ∠BAC=180 °
所以∠BAC= 180 ° - ∠B - ∠C= 180 ° - 46 ° - 54 °= 80 °
因为AD是 △ABC的角平分线,
所以∠BAD= ∠BAC= × 80 °=40°
又因为∠ADE是△ABD的一个外角
所以∠ADE= ∠B+ ∠BAD = 46 ° + 40°= 86 °
(3)在直角三角形ADE中, ∠ADE+ ∠DAE= 90°
所以 ∠DAE= 90° - ∠ADE = 90° - 86 ° = 4°
(直角三角形两锐角互余)
(直角三角形两锐角互余)
(三角形的内角和等于180 °)
(三角形的一个外角等于与它不相邻的两个内角的和)
(角平分线的定义)
课 堂 小 结
(1)重点探究了三角形3个内角之间的
关系以及三角形外角的性质.
三角形3个内角的和等于180°.
三角形的一个外角等于与它不相邻的两个内角的和.
(2)由三角形3个内角之间的关系得到直
角三角形的一个性质:
直角三角形的两个锐角互余.
谢谢观看
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
