1 锐角三角函数 课件(16张PPT)
文档属性
| 名称 | 1 锐角三角函数 课件(16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 540.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-12 00:00:00 | ||
图片预览



文档简介
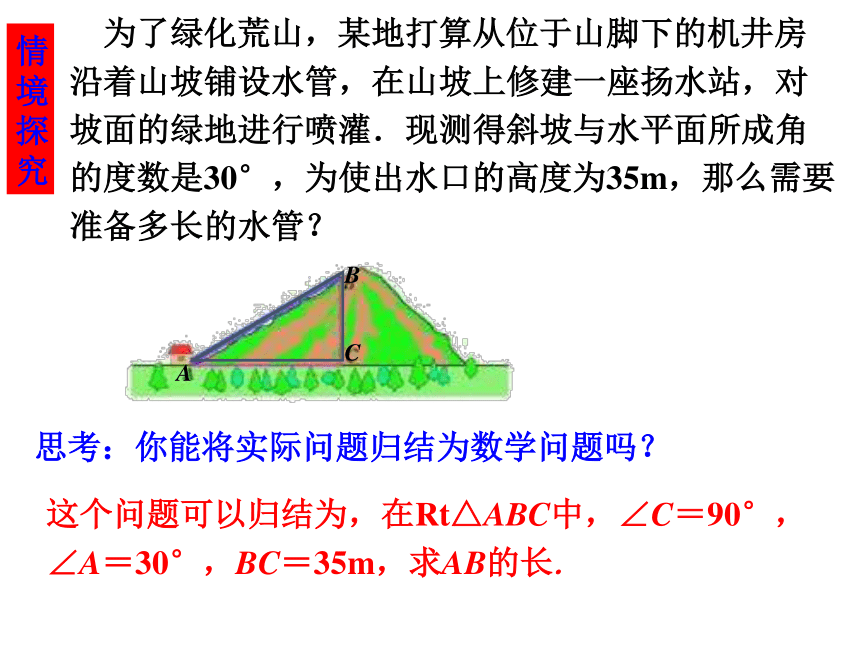
为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?
这个问题可以归结为,在Rt△ABC中,∠C=90°,∠A=30°,BC=35m,求AB的长.
A
B
C
思考:你能将实际问题归结为数学问题吗?
情境探究
根据“在直角三角形中,30°角所对的直角边等于斜边的一半”,即
A
B
C
在Rt△ABC中,∠C=90°,∠A=30°,BC=35m,求AB的长.
可得 AB=2BC=70m,即需要准备70m长的水管.
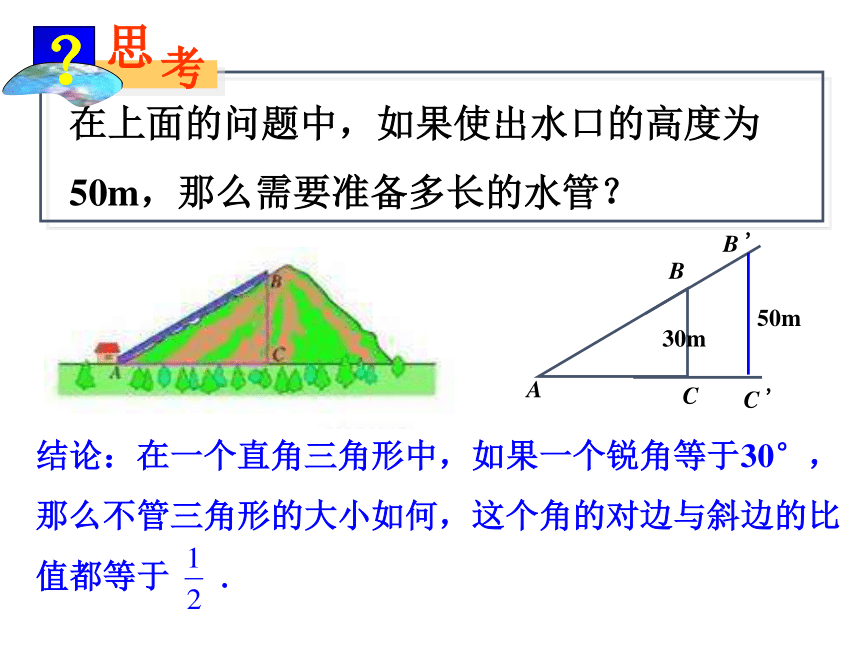
在上面的问题中,如果使出水口的高度为50m,那么需要准备多长的水管?
结论:在一个直角三角形中,如果一个锐角等于30°,那么不管三角形的大小如何,这个角的对边与斜边的比值都等于 .
A
B
C
50m
30m
B '
C '
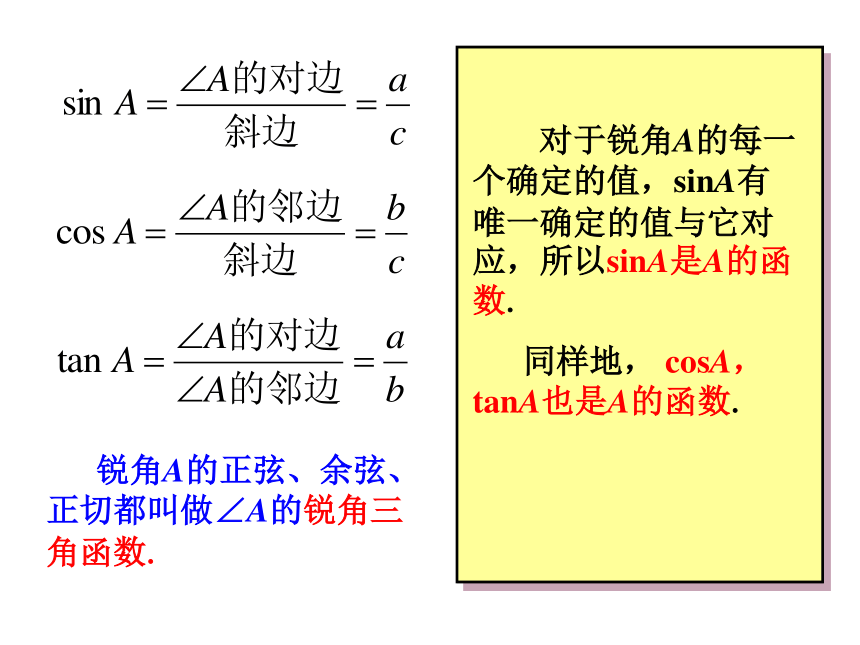
对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.
同样地, cosA,tanA也是A的函数.
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
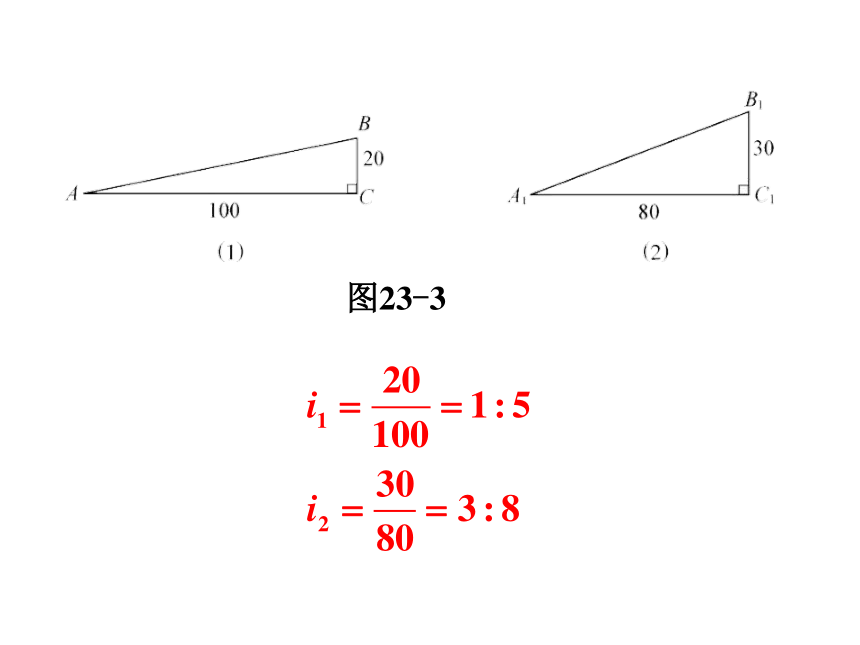
1.计算图23-2、图23-3中坡面AB和A1B1的坡度.
图23-2
图23-3
下图表示两个自动扶梯,那一个自动扶梯比较陡?
解:甲梯中,
β
6m
┐
乙
8m
α
5m
┌
甲
13m
乙梯中,
∵tanβ>tanα,∴乙梯更陡.
老师提示:
生活中,常用一个锐角的正切表示梯子的倾斜程度.
例 题 示 范
例 如图,在Rt△ABC中,∠C=90°,AB=5 ,AC=2.求sinA和sinB的值.
例 题 示 范
A
C
B
解:如图,在Rt△ABC中
练习
A
C
3
5
B
2、在平面直角平面坐标系中,已知点A(3,0)
和B(0,-4),则sin∠OAB等于____.
3、在Rt△ABC中,∠C=90°,AD是BC边
上的中线,AC=2,BC=4,则sin∠DAC=___.
1、如图,求sinA和sinB的值.
在Rt△ABC中,∠C=90°,AB=15,tanA= ,
求AC和BC.
在等△ABC,AB=AC=13,BC=10,
求tanB.
老师提示:
过点A作AD垂直于BC于点D.
求锐角三角函数时,勾股定理的运用是很重要的.
A
C
B
┌
D
C
A
B
10
6
如图,△ABC是直角三角形,∠C=90°,AB=10,AC=6.求sinA、cosA、tanA、sinB、cosB、tanB.
解:由题意得
BC2=AB2-AC2,
BC=8,
A
B
C
6
如图,在Rt△ABC中,∠C=90°,BC=6, ,求cosA和tanB的值.
如图,在Rt△ABC中,∠C=90°,BC=2,AB=3,求∠A,∠B的正弦、余弦、正切值.
A
B
C
2
3
延伸:由上面的计算,你能猜想∠A,∠B的正弦、余弦值有什么规律吗?
结论:一个锐角的正弦等于它余角的余弦,或一个锐角的余弦等于它余角的正弦.
想一想你学到了什么?
这个问题可以归结为,在Rt△ABC中,∠C=90°,∠A=30°,BC=35m,求AB的长.
A
B
C
思考:你能将实际问题归结为数学问题吗?
情境探究
根据“在直角三角形中,30°角所对的直角边等于斜边的一半”,即
A
B
C
在Rt△ABC中,∠C=90°,∠A=30°,BC=35m,求AB的长.
可得 AB=2BC=70m,即需要准备70m长的水管.
在上面的问题中,如果使出水口的高度为50m,那么需要准备多长的水管?
结论:在一个直角三角形中,如果一个锐角等于30°,那么不管三角形的大小如何,这个角的对边与斜边的比值都等于 .
A
B
C
50m
30m
B '
C '
对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.
同样地, cosA,tanA也是A的函数.
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
1.计算图23-2、图23-3中坡面AB和A1B1的坡度.
图23-2
图23-3
下图表示两个自动扶梯,那一个自动扶梯比较陡?
解:甲梯中,
β
6m
┐
乙
8m
α
5m
┌
甲
13m
乙梯中,
∵tanβ>tanα,∴乙梯更陡.
老师提示:
生活中,常用一个锐角的正切表示梯子的倾斜程度.
例 题 示 范
例 如图,在Rt△ABC中,∠C=90°,AB=5 ,AC=2.求sinA和sinB的值.
例 题 示 范
A
C
B
解:如图,在Rt△ABC中
练习
A
C
3
5
B
2、在平面直角平面坐标系中,已知点A(3,0)
和B(0,-4),则sin∠OAB等于____.
3、在Rt△ABC中,∠C=90°,AD是BC边
上的中线,AC=2,BC=4,则sin∠DAC=___.
1、如图,求sinA和sinB的值.
在Rt△ABC中,∠C=90°,AB=15,tanA= ,
求AC和BC.
在等△ABC,AB=AC=13,BC=10,
求tanB.
老师提示:
过点A作AD垂直于BC于点D.
求锐角三角函数时,勾股定理的运用是很重要的.
A
C
B
┌
D
C
A
B
10
6
如图,△ABC是直角三角形,∠C=90°,AB=10,AC=6.求sinA、cosA、tanA、sinB、cosB、tanB.
解:由题意得
BC2=AB2-AC2,
BC=8,
A
B
C
6
如图,在Rt△ABC中,∠C=90°,BC=6, ,求cosA和tanB的值.
如图,在Rt△ABC中,∠C=90°,BC=2,AB=3,求∠A,∠B的正弦、余弦、正切值.
A
B
C
2
3
延伸:由上面的计算,你能猜想∠A,∠B的正弦、余弦值有什么规律吗?
结论:一个锐角的正弦等于它余角的余弦,或一个锐角的余弦等于它余角的正弦.
想一想你学到了什么?
