1 锐角三角函数 课件(18张PPT)
文档属性
| 名称 | 1 锐角三角函数 课件(18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 777.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-12 00:00:00 | ||
图片预览



文档简介
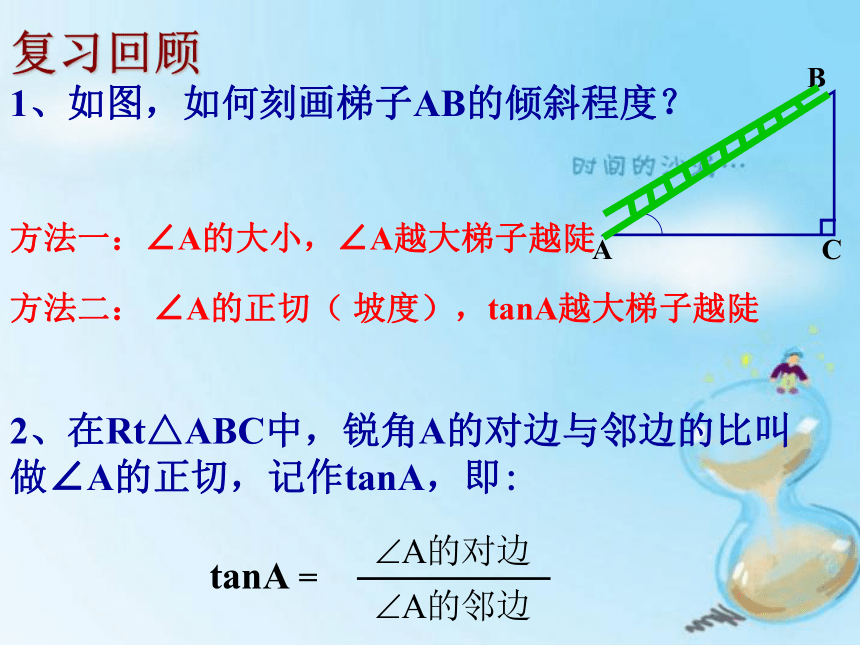
方法一:∠A的大小,∠A越大梯子越陡
复习回顾
2、在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即:
A
B
C
┌
1、如图,如何刻画梯子AB的倾斜程度?
方法二: ∠A的正切( 坡度),tanA越大梯子越陡
tanA =
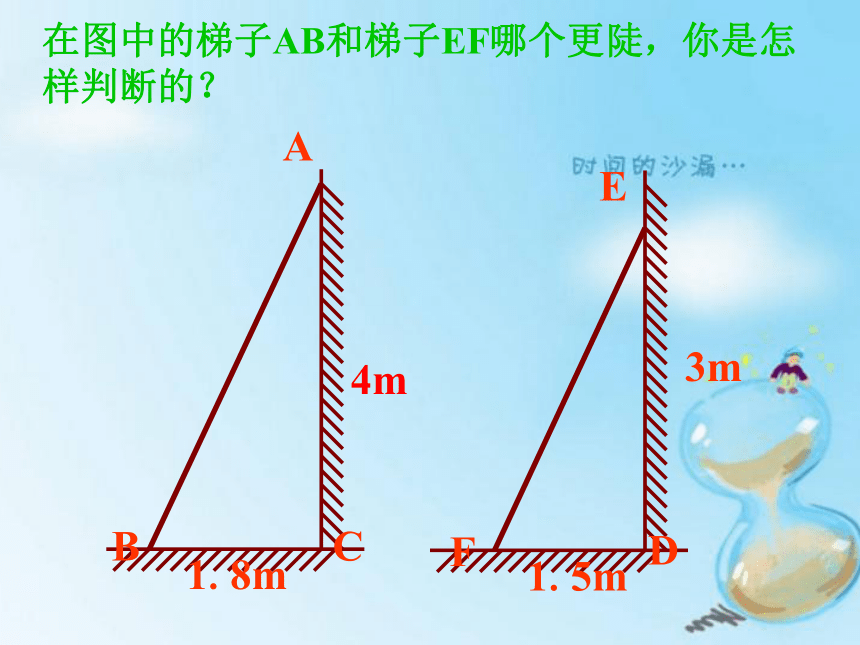
1.8m
A
C
B
1.5m
E
3m
D
F
在图中的梯子AB和梯子EF哪个更陡,你是怎样判断的?
4m
A
B
C
D
E
F
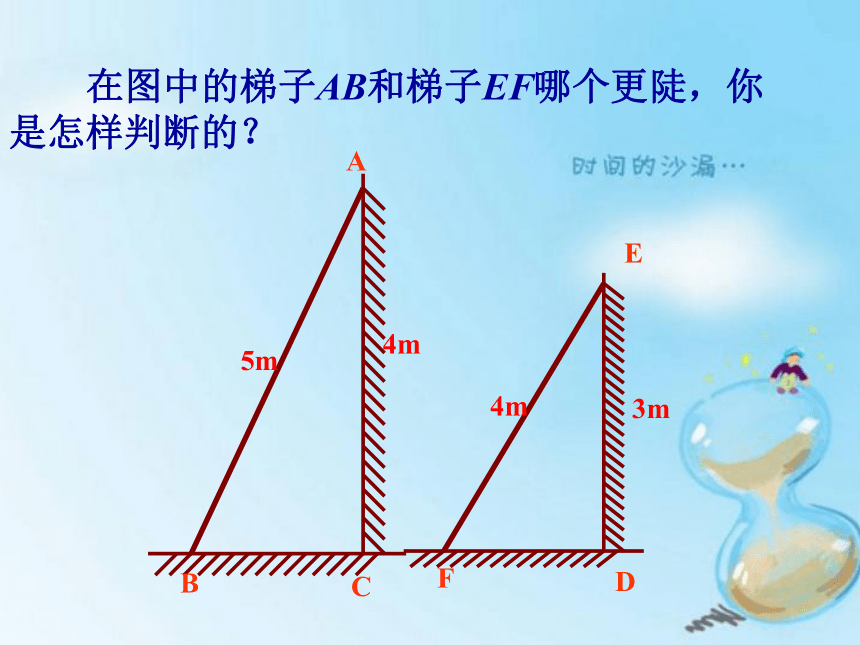
4m
5m
3m
4m
在图中的梯子AB和梯子EF哪个更陡,你是怎样判断的?
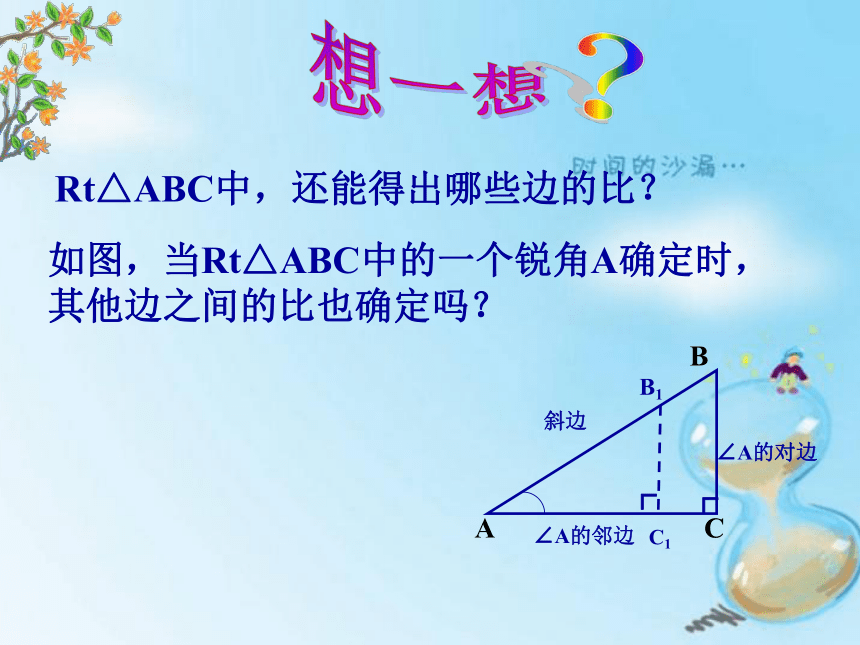
如图,当Rt△ABC中的一个锐角A确定时,其他边之间的比也确定吗?
A
B
C
┌
∠A的邻边
斜边
∠A的对边
C1
B1
Rt△ABC中,还能得出哪些边的比?
┌
在Rt△ABC中,锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即
锐角A的正弦,余弦和正切都是做∠A的三角函数.
在Rt△ABC中,锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即
A
B
C
┌
∠A的邻边
斜边
∠A的对边
1.如图, sinA=____,
cosA=______
cosC=_______
C
┌
A
B
2
5
2
2
5
2
2
A
2
A
B
C
2.如图,在Rt△ABC中AC=12,AB=5,则
tanB=_______
sinB=______, sinC=_________
cosB_______,cosC=__________
5
12
2.4
3.已知∠A,∠D为锐角
(1)若∠A=∠D,则sinA sinD;
(2)若cosA=cosD,则∠A ∠D.
=
=
C
┌
D
E
F
┌
A
B
4.如图:在等腰△ABC中,AB=AC=5,BC=6.
求: sinB,cosB,tanB.
5
5
A
B
C
D
6
如图:在Rt△ABC中,∠B=90°,AC=200,sinA=0.6.
求:BC的长.
200
A
C
B
┌
?
怎样解答
求:AB,sinB.
10
┐
A
B
C
如图:在Rt△ABC中,∠C=90°,AC=10,
注意到这里cosA和sinB,其中有没有什么内有的关系?
做一做
梯子的倾斜程度与sinA和cosA有关:
如图,梯子的倾斜程度与sinA和cosA有关吗?
cosA越小,梯子越陡.
sinA越大,梯子越陡;
议一议
结论:正弦、余弦、正切都可以刻画梯子的倾斜程度
A
B
A1
B1
A1
B1
A1
C
A
B
C
D
E
F
4m
5m
3m
4m
在图中的梯子AB和梯子EF哪个更陡,你是怎样判断的?
随着人民生活水平的提高,私家车的数量越来越多,现在某小区就面临停车难的问题,如图,是供机动车停放的示意图,请你参考图中数据,计算车位所占街道的宽度DB.
C
2m
5m
A
B
D
E
F
将本课所学知识
纳入知识体系
小结
1、锐角A的正弦,余弦和正切都是做∠A的三角函数.
2、若∠A+ ∠B=90°,则 sinA=cosB,cosA=sinB
3、sinA越大,梯子越陡; cosA越小,梯子越陡.
祝你成功!
复习回顾
2、在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即:
A
B
C
┌
1、如图,如何刻画梯子AB的倾斜程度?
方法二: ∠A的正切( 坡度),tanA越大梯子越陡
tanA =
1.8m
A
C
B
1.5m
E
3m
D
F
在图中的梯子AB和梯子EF哪个更陡,你是怎样判断的?
4m
A
B
C
D
E
F
4m
5m
3m
4m
在图中的梯子AB和梯子EF哪个更陡,你是怎样判断的?
如图,当Rt△ABC中的一个锐角A确定时,其他边之间的比也确定吗?
A
B
C
┌
∠A的邻边
斜边
∠A的对边
C1
B1
Rt△ABC中,还能得出哪些边的比?
┌
在Rt△ABC中,锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即
锐角A的正弦,余弦和正切都是做∠A的三角函数.
在Rt△ABC中,锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即
A
B
C
┌
∠A的邻边
斜边
∠A的对边
1.如图, sinA=____,
cosA=______
cosC=_______
C
┌
A
B
2
5
2
2
5
2
2
A
2
A
B
C
2.如图,在Rt△ABC中AC=12,AB=5,则
tanB=_______
sinB=______, sinC=_________
cosB_______,cosC=__________
5
12
2.4
3.已知∠A,∠D为锐角
(1)若∠A=∠D,则sinA sinD;
(2)若cosA=cosD,则∠A ∠D.
=
=
C
┌
D
E
F
┌
A
B
4.如图:在等腰△ABC中,AB=AC=5,BC=6.
求: sinB,cosB,tanB.
5
5
A
B
C
D
6
如图:在Rt△ABC中,∠B=90°,AC=200,sinA=0.6.
求:BC的长.
200
A
C
B
┌
?
怎样解答
求:AB,sinB.
10
┐
A
B
C
如图:在Rt△ABC中,∠C=90°,AC=10,
注意到这里cosA和sinB,其中有没有什么内有的关系?
做一做
梯子的倾斜程度与sinA和cosA有关:
如图,梯子的倾斜程度与sinA和cosA有关吗?
cosA越小,梯子越陡.
sinA越大,梯子越陡;
议一议
结论:正弦、余弦、正切都可以刻画梯子的倾斜程度
A
B
A1
B1
A1
B1
A1
C
A
B
C
D
E
F
4m
5m
3m
4m
在图中的梯子AB和梯子EF哪个更陡,你是怎样判断的?
随着人民生活水平的提高,私家车的数量越来越多,现在某小区就面临停车难的问题,如图,是供机动车停放的示意图,请你参考图中数据,计算车位所占街道的宽度DB.
C
2m
5m
A
B
D
E
F
将本课所学知识
纳入知识体系
小结
1、锐角A的正弦,余弦和正切都是做∠A的三角函数.
2、若∠A+ ∠B=90°,则 sinA=cosB,cosA=sinB
3、sinA越大,梯子越陡; cosA越小,梯子越陡.
祝你成功!
