2 反比例函数的图像与性质 课件(23张PPT)
文档属性
| 名称 | 2 反比例函数的图像与性质 课件(23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-12 09:01:41 | ||
图片预览







文档简介
1. 反比例函数的定义:
3. 反比例函数的确定:
4.它的三种常见的表达形式:
2. 反比例函数的特征:
叫做反比例函数.
函数
k ≠0, x ≠0. x是-1次
待定系数法.
xy = k(k ≠ 0)
y=kx-1(k≠0)
复习回顾,引入新课
1、下列函数中哪些是y关于x的反比例函数?
① ② ③ ④
⑤ ⑥ ⑦ ⑧
y = 3x-1
y = 2x -1
y =
y =
y =
y =
y =
2、已知△ABC的面积为12,则△ABC的高h与它的底边a的函数关系式为:
3、已知Y是X的反比例函数,下表给出了X和Y的一些值:
X
-2
-1
1
3
Y
2
-1
(1)求出这个反比例函数的解析式
思考:表中能否增加X=0或Y=0的值,为什么?
(2)根据函数解析式完成上表
1
-2
2
函数图象画法
列
表
描
点
连
线
描点法
反比例函数的图象又会是什么样子呢?
你还记得作函数图象的一般步骤吗?
用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线(按自变量从小到大的顺序,用一条平滑的曲线连接起来).
列表
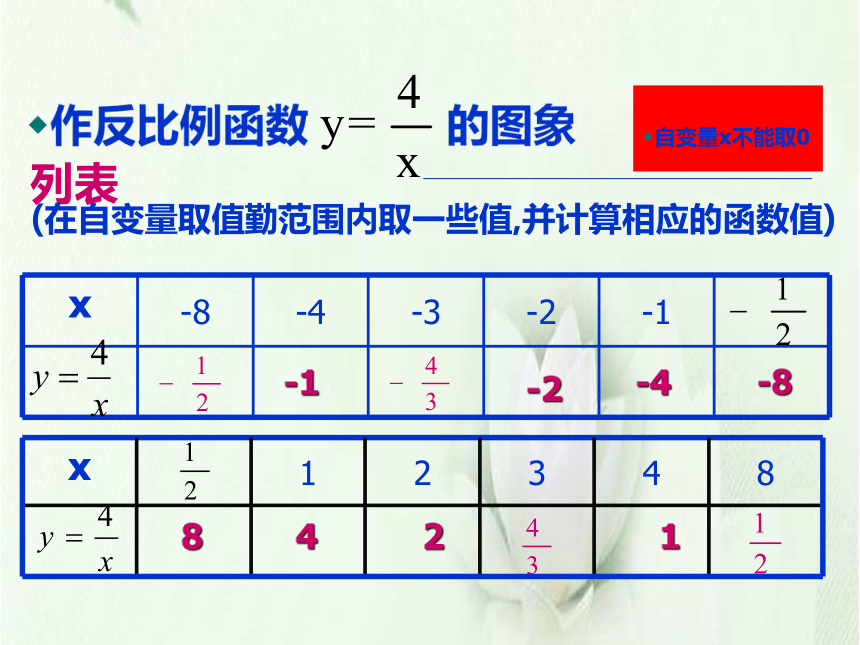
(在自变量取值勤范围内取一些值,并计算相应的函数值)
x
-8
-4
-3
-2
-1
-1
-2
-4
-8
作反比例函数 的图象
x
1
2
3
4
8
8
4
2
1
自变量x不能取0
思考:1、你认为作反比例函数图象是应注意哪些问题?
描点
连线
从画反比例函数图象看,描点法还应注意什么?
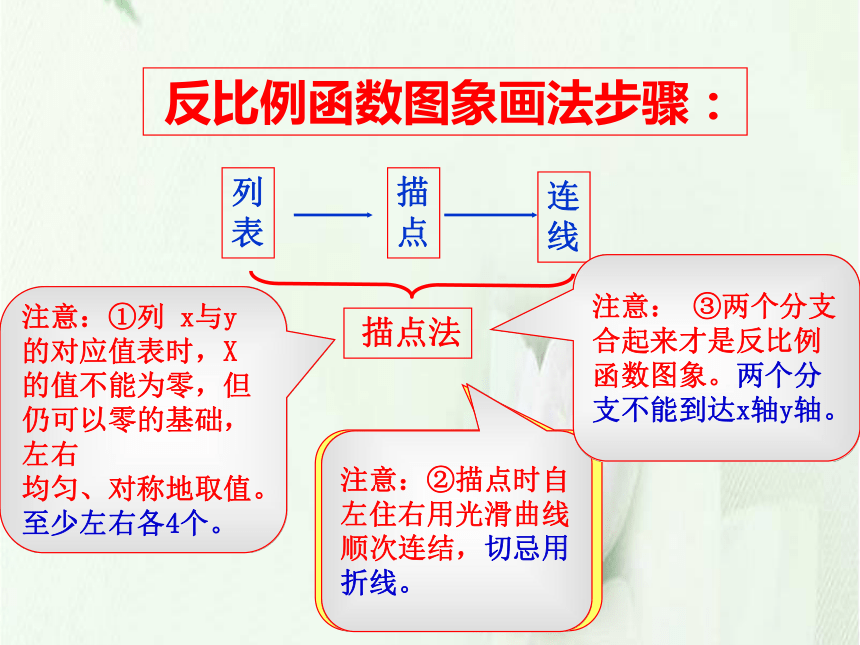
反比例函数图象画法步骤:
列
表
描
点
连
线
描点法
注意:①列 x与y的对应值表时,X的值不能为零,但仍可以零的基础,左右
均匀、对称地取值。
至少左右各4个。
注意:②描点时自左住右用光滑曲线顺次连结,切忌用折线。
注意: ③两个分支合起来才是反比例函数图象。两个分支不能到达x轴y轴。
2. 反比例函数 的图象在哪两个象限?由什么确定?
3. 反比例函数 ,具有怎样的对称性?
4. 反比例函数 的图象的变化趋势是怎样的,它和两条坐标轴的位置关系是怎样的?
1. 反比例函数 和 的图象在哪两个象限?它们相同吗?
x
y
0
y
x
y
0
议一议:
讨 论
反比例函数的性质
1.当k>0时,图象的两个分支分别在第一、三象限内;
2.当k<0时,图象的两个分支分别在第二、四象限内。
x
y
0
y
x
y
0
3.图象的两个分支关于直角坐标系的原点成中心对称。
x
0
如果知道双曲线的一支,利用对称性,如何画另一支?
4.双曲线无限接近于x、y轴,但永远不会与坐标轴相交
你能总结一下反比例函数的图象性质特征吗?
图象是双曲线
当k>0时,双曲线分别位于第一,三象限内
当k<0时, 双曲线分别位于第二,四象限内
双曲线是中心对称图形.
形状
位置
变化趋势
对称性
形 状
位 置
变化趋势
对称性
双曲线无限接近于x、y轴,但永远不会
与坐标轴相交
对称中心是:
坐标原点
1.函数 的图象在第_____象限,
2. 双曲线 经过点(-3,___)
练习 1
二,四
9
1
3.函数 的图象在二、四象限,则m的取值范围是 ____ .
4.对于函数 ,当 x<0时,图象在第 ________象限.
m < 2
三
5. 已知反比例函数 的图像在二、四象限内,而一次函数y=mx+2的图象经过一、二、三象限,求m的取值范围.
6.在平面直角坐标系中有六个点 A(1,5),
B(-3,-1.5),C(-5,-1),
D(2,5/2),E(3,5/3),
F(5/2,2),其中有五个点在同一反比例函数图像上,在这个反比例函数图像上的点 有 ( )
已知反比例函数y= (k≠0)的图象的一支如图。
(1)判断k是正数还是负数;
(2)求这个反比例函数的解析式;
y
x
0
(-4,2)
(3)补画这个反比例函数图象的另一支。
x
0
(-4,2)
y
例题解析,当堂练习
1、下列反比例函数的图象分别在哪个象限?
⑴ ⑵
做一做:
2、已知反比例函数 (k≠0) 的图象上
一点的坐标为( ,2 )。
求这个反比例函数的解析式。
任意一组变量的乘积是一个定值,即xy=k
P(m,n)
A
o
y
x
B
长方形面积 ︳m n︱ =︳K︱
三角形的面积
面积不变性
1.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .
2.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .
P
D
o
y
x
x
y
o
M
N
p
2
x
y
A
B
C
D
O
B
相交于A、B两点.过 A作x轴的垂线、过B
作y轴的垂线,垂足分别为D、C,设梯形ABCD的
面积为S,则( )
A.S=6 B.S=3
C.23. 如图,正比例函数 与反比例函数
梳理概括,形成结构
请大家围绕以下三个问题小结本节课
① 什么是反比例函数?
② 反比例函数的图象是什么样子的?怎样作图象
③ 反比例函数的性质是什么?
形状
位置
变化趋势
对称性
面积不变性
x
y
0
K>0
拓展:
1、在直角坐标系中,直线y=x+m-1与双曲线 在第一象限交于点A,与x轴交于点C,AB垂直于x轴,垂足为B,且S△AOB=2
(1)求m的值;
(2)求△ABC的面积。
(1)m=4
(2) S△ABC=8
y
x
O
A
B
C
①已知y 与 x 成反比例, 并且当 x = 3 时
y = 7,求 x 与 y 的函数关系式。
③已知y 与 x2 成反比例, 并且当 x = 3时
y = 4,求 x = 1.5 时 y的值.
②根据图形写出函数的解析式.
y
x
y
0
(-3,1)
3. 反比例函数的确定:
4.它的三种常见的表达形式:
2. 反比例函数的特征:
叫做反比例函数.
函数
k ≠0, x ≠0. x是-1次
待定系数法.
xy = k(k ≠ 0)
y=kx-1(k≠0)
复习回顾,引入新课
1、下列函数中哪些是y关于x的反比例函数?
① ② ③ ④
⑤ ⑥ ⑦ ⑧
y = 3x-1
y = 2x -1
y =
y =
y =
y =
y =
2、已知△ABC的面积为12,则△ABC的高h与它的底边a的函数关系式为:
3、已知Y是X的反比例函数,下表给出了X和Y的一些值:
X
-2
-1
1
3
Y
2
-1
(1)求出这个反比例函数的解析式
思考:表中能否增加X=0或Y=0的值,为什么?
(2)根据函数解析式完成上表
1
-2
2
函数图象画法
列
表
描
点
连
线
描点法
反比例函数的图象又会是什么样子呢?
你还记得作函数图象的一般步骤吗?
用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线(按自变量从小到大的顺序,用一条平滑的曲线连接起来).
列表
(在自变量取值勤范围内取一些值,并计算相应的函数值)
x
-8
-4
-3
-2
-1
-1
-2
-4
-8
作反比例函数 的图象
x
1
2
3
4
8
8
4
2
1
自变量x不能取0
思考:1、你认为作反比例函数图象是应注意哪些问题?
描点
连线
从画反比例函数图象看,描点法还应注意什么?
反比例函数图象画法步骤:
列
表
描
点
连
线
描点法
注意:①列 x与y的对应值表时,X的值不能为零,但仍可以零的基础,左右
均匀、对称地取值。
至少左右各4个。
注意:②描点时自左住右用光滑曲线顺次连结,切忌用折线。
注意: ③两个分支合起来才是反比例函数图象。两个分支不能到达x轴y轴。
2. 反比例函数 的图象在哪两个象限?由什么确定?
3. 反比例函数 ,具有怎样的对称性?
4. 反比例函数 的图象的变化趋势是怎样的,它和两条坐标轴的位置关系是怎样的?
1. 反比例函数 和 的图象在哪两个象限?它们相同吗?
x
y
0
y
x
y
0
议一议:
讨 论
反比例函数的性质
1.当k>0时,图象的两个分支分别在第一、三象限内;
2.当k<0时,图象的两个分支分别在第二、四象限内。
x
y
0
y
x
y
0
3.图象的两个分支关于直角坐标系的原点成中心对称。
x
0
如果知道双曲线的一支,利用对称性,如何画另一支?
4.双曲线无限接近于x、y轴,但永远不会与坐标轴相交
你能总结一下反比例函数的图象性质特征吗?
图象是双曲线
当k>0时,双曲线分别位于第一,三象限内
当k<0时, 双曲线分别位于第二,四象限内
双曲线是中心对称图形.
形状
位置
变化趋势
对称性
形 状
位 置
变化趋势
对称性
双曲线无限接近于x、y轴,但永远不会
与坐标轴相交
对称中心是:
坐标原点
1.函数 的图象在第_____象限,
2. 双曲线 经过点(-3,___)
练习 1
二,四
9
1
3.函数 的图象在二、四象限,则m的取值范围是 ____ .
4.对于函数 ,当 x<0时,图象在第 ________象限.
m < 2
三
5. 已知反比例函数 的图像在二、四象限内,而一次函数y=mx+2的图象经过一、二、三象限,求m的取值范围.
6.在平面直角坐标系中有六个点 A(1,5),
B(-3,-1.5),C(-5,-1),
D(2,5/2),E(3,5/3),
F(5/2,2),其中有五个点在同一反比例函数图像上,在这个反比例函数图像上的点 有 ( )
已知反比例函数y= (k≠0)的图象的一支如图。
(1)判断k是正数还是负数;
(2)求这个反比例函数的解析式;
y
x
0
(-4,2)
(3)补画这个反比例函数图象的另一支。
x
0
(-4,2)
y
例题解析,当堂练习
1、下列反比例函数的图象分别在哪个象限?
⑴ ⑵
做一做:
2、已知反比例函数 (k≠0) 的图象上
一点的坐标为( ,2 )。
求这个反比例函数的解析式。
任意一组变量的乘积是一个定值,即xy=k
P(m,n)
A
o
y
x
B
长方形面积 ︳m n︱ =︳K︱
三角形的面积
面积不变性
1.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .
2.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .
P
D
o
y
x
x
y
o
M
N
p
2
x
y
A
B
C
D
O
B
相交于A、B两点.过 A作x轴的垂线、过B
作y轴的垂线,垂足分别为D、C,设梯形ABCD的
面积为S,则( )
A.S=6 B.S=3
C.2
梳理概括,形成结构
请大家围绕以下三个问题小结本节课
① 什么是反比例函数?
② 反比例函数的图象是什么样子的?怎样作图象
③ 反比例函数的性质是什么?
形状
位置
变化趋势
对称性
面积不变性
x
y
0
K>0
拓展:
1、在直角坐标系中,直线y=x+m-1与双曲线 在第一象限交于点A,与x轴交于点C,AB垂直于x轴,垂足为B,且S△AOB=2
(1)求m的值;
(2)求△ABC的面积。
(1)m=4
(2) S△ABC=8
y
x
O
A
B
C
①已知y 与 x 成反比例, 并且当 x = 3 时
y = 7,求 x 与 y 的函数关系式。
③已知y 与 x2 成反比例, 并且当 x = 3时
y = 4,求 x = 1.5 时 y的值.
②根据图形写出函数的解析式.
y
x
y
0
(-3,1)
