3 用计算器求锐角的三角函数值 课件(13张)
文档属性
| 名称 | 3 用计算器求锐角的三角函数值 课件(13张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-12 00:00:00 | ||
图片预览




文档简介
用计算器求锐角的三角函数值
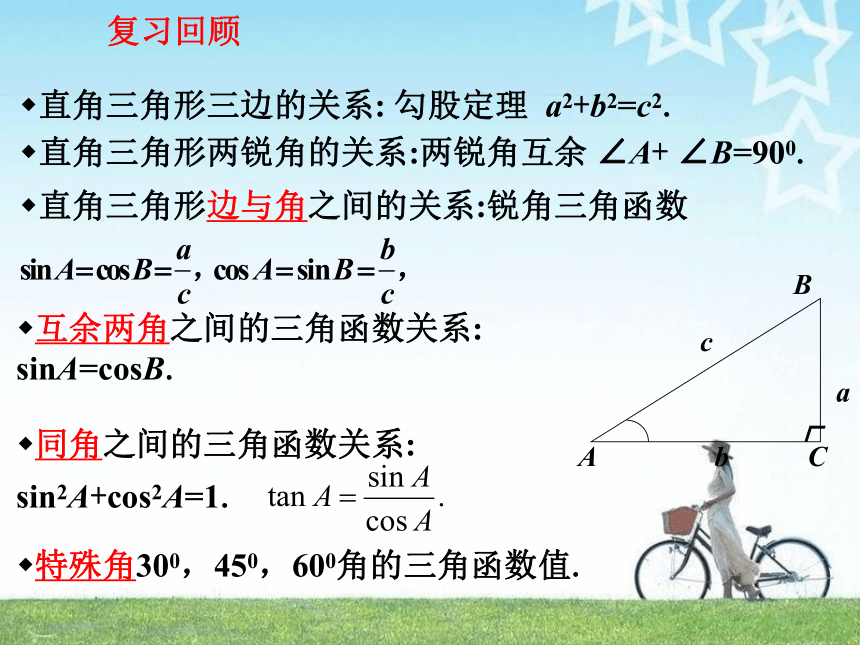
直角三角形两锐角的关系:两锐角互余 ∠A+ ∠B=900.
直角三角形三边的关系: 勾股定理 a2+b2=c2.
b
A
B
C
a
┌
c
互余两角之间的三角函数关系:
sinA=cosB.
特殊角300,450,600角的三角函数值.
直角三角形边与角之间的关系:锐角三角函数
同角之间的三角函数关系:
sin2A+cos2A=1.
复习回顾
如图,为了方便行人,市政府在10m高的天桥两端修建了40m长的斜道.这条斜道的倾斜角是多少?
那么∠A是多少度呢?
要解决这问题,我们可以借助科学计算器.
请与同伴交流你是怎么做的?
如图,在Rt△ABC中,
引入新知
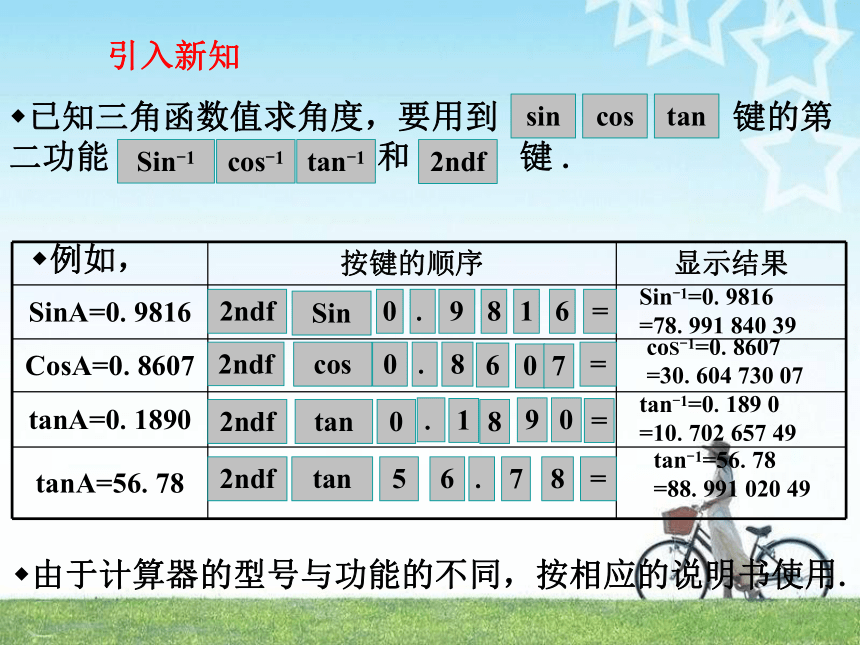
已知三角函数值求角度,要用到 键的第二功能 和 键 .
例如,
由于计算器的型号与功能的不同,按相应的说明书使用.
sin
cos
tan
按键的顺序
显示结果
SinA=0.9816
CosA=0.8607
tanA=0.1890
tanA=56.78
2ndf
Sin
0
.
Sin-1=0.9816
=78.991 840 39
2ndf
cos
0
.
coS-1=0.8607
=30.604 730 07
2ndf
tan
0
.
tan-1=0.189 0
=10.702 657 49
2ndf
tan
5
6
.
7
8
tan-1=56.78
=88.991 020 49
9
8
1
=
Sin-1
cos-1
tan-1
2ndf
8
1
6
=
6
0
7
=
8
9
0
=
引入新知
1 根据下列条件求∠θ的大小:
(1)tanθ=2.988 8; (2)sinθ=0.395 7;
(3)cosθ=0.785 0; (4)tanθ=0.897 2.
老师提示:上表的显示结果是以度为单位的,再按 键即可显示以“度,分,秒”为单位的结果.
dms
练一练
例1 如图,工件上有一V型槽,测得它的上口宽20mm,深19.2mm.求V型角(∠ACB)的大小(结果精确到1°).
∴∠ACD≈27.5° .
∴∠ACB=2∠ACD≈2×27.5°=55°.
∴V型角的大小约55°.
例题解析
2 一辆汽车沿着一山坡行驶了1000m,其铅直高度上升了50m.求山坡与水平面所成的锐角的大小.
练一练
例2 如图,一名患者体内某重要器官后面有一肿瘤.在接受放射性治疗时,为了最大限度地保证疗效,并且防止伤害器官,射线必需从侧面照射肿瘤.已知肿瘤在皮下6.3cm的A处,射线从肿瘤右侧9.8cm的B处进入身体,求射线的入射角度.
解:如图,在Rt△ABC中,AC=6.3cm,BC=9.8cm,
∴∠B≈32° 44′13″.
因此,射线的入射角度约为32°44′13″.
例题解析
1. 已知sinθ=0.82904,求∠θ的大小.
老师期望:
先将实际问题数学化,然后运用所学知识予以解答.
2. 一梯子斜靠在一面墙上,已知梯子长4m,梯子位于地面上的一端离墙壁2.5m,求梯子与地面所成的锐角.
课后练习
3. 图中的螺旋形由一系列直角三角形组成.每个三角形都以点O为一顶点.
(1)求∠A0OA1,∠A1OA2,∠A2OA3,的大小.
(2)已知∠An-1OAn,是一个小于20°的角,求n的值.
课后练习
由锐角的三角函数值反求锐角
小结 拓展
填表:已知一个角的三角函数值,求这个角的度数(逆向思维)
∠A=
∠A=
∠A=
∠A=
∠A=
∠A=
∠A=
∠A=
∠A=
直角三角形两锐角的关系:两锐角互余 ∠A+ ∠B=900.
直角三角形三边的关系: 勾股定理 a2+b2=c2.
b
A
B
C
a
┌
c
互余两角之间的三角函数关系:
sinA=cosB.
特殊角300,450,600角的三角函数值.
直角三角形边与角之间的关系:锐角三角函数
同角之间的三角函数关系:
sin2A+cos2A=1.
复习回顾
如图,为了方便行人,市政府在10m高的天桥两端修建了40m长的斜道.这条斜道的倾斜角是多少?
那么∠A是多少度呢?
要解决这问题,我们可以借助科学计算器.
请与同伴交流你是怎么做的?
如图,在Rt△ABC中,
引入新知
已知三角函数值求角度,要用到 键的第二功能 和 键 .
例如,
由于计算器的型号与功能的不同,按相应的说明书使用.
sin
cos
tan
按键的顺序
显示结果
SinA=0.9816
CosA=0.8607
tanA=0.1890
tanA=56.78
2ndf
Sin
0
.
Sin-1=0.9816
=78.991 840 39
2ndf
cos
0
.
coS-1=0.8607
=30.604 730 07
2ndf
tan
0
.
tan-1=0.189 0
=10.702 657 49
2ndf
tan
5
6
.
7
8
tan-1=56.78
=88.991 020 49
9
8
1
=
Sin-1
cos-1
tan-1
2ndf
8
1
6
=
6
0
7
=
8
9
0
=
引入新知
1 根据下列条件求∠θ的大小:
(1)tanθ=2.988 8; (2)sinθ=0.395 7;
(3)cosθ=0.785 0; (4)tanθ=0.897 2.
老师提示:上表的显示结果是以度为单位的,再按 键即可显示以“度,分,秒”为单位的结果.
dms
练一练
例1 如图,工件上有一V型槽,测得它的上口宽20mm,深19.2mm.求V型角(∠ACB)的大小(结果精确到1°).
∴∠ACD≈27.5° .
∴∠ACB=2∠ACD≈2×27.5°=55°.
∴V型角的大小约55°.
例题解析
2 一辆汽车沿着一山坡行驶了1000m,其铅直高度上升了50m.求山坡与水平面所成的锐角的大小.
练一练
例2 如图,一名患者体内某重要器官后面有一肿瘤.在接受放射性治疗时,为了最大限度地保证疗效,并且防止伤害器官,射线必需从侧面照射肿瘤.已知肿瘤在皮下6.3cm的A处,射线从肿瘤右侧9.8cm的B处进入身体,求射线的入射角度.
解:如图,在Rt△ABC中,AC=6.3cm,BC=9.8cm,
∴∠B≈32° 44′13″.
因此,射线的入射角度约为32°44′13″.
例题解析
1. 已知sinθ=0.82904,求∠θ的大小.
老师期望:
先将实际问题数学化,然后运用所学知识予以解答.
2. 一梯子斜靠在一面墙上,已知梯子长4m,梯子位于地面上的一端离墙壁2.5m,求梯子与地面所成的锐角.
课后练习
3. 图中的螺旋形由一系列直角三角形组成.每个三角形都以点O为一顶点.
(1)求∠A0OA1,∠A1OA2,∠A2OA3,的大小.
(2)已知∠An-1OAn,是一个小于20°的角,求n的值.
课后练习
由锐角的三角函数值反求锐角
小结 拓展
填表:已知一个角的三角函数值,求这个角的度数(逆向思维)
∠A=
∠A=
∠A=
∠A=
∠A=
∠A=
∠A=
∠A=
∠A=
