4 解直角三角形 课件(12张PPT)
文档属性
| 名称 | 4 解直角三角形 课件(12张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 689.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-12 09:01:41 | ||
图片预览





文档简介
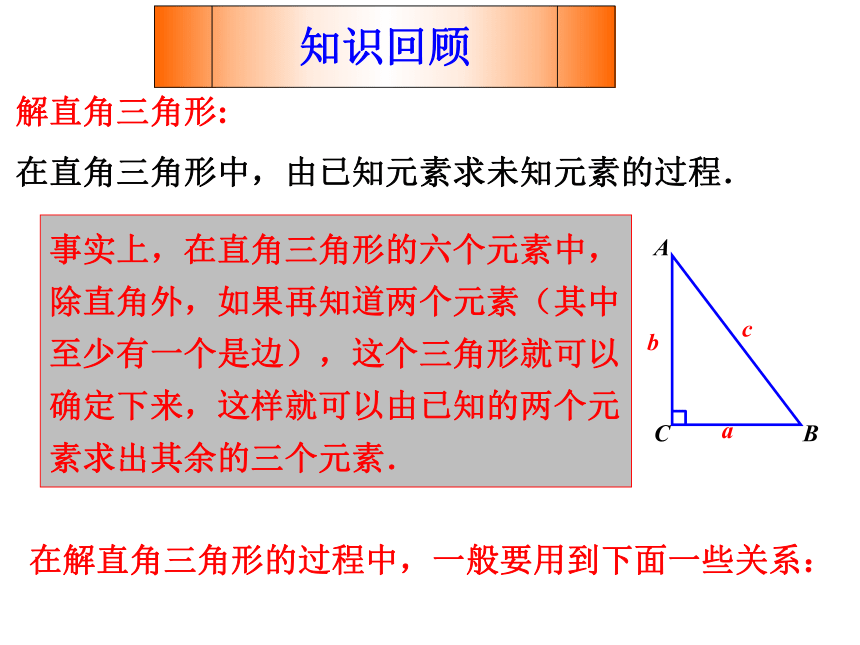
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
A
B
a
b
c
C
解直角三角形:
在直角三角形中,由已知元素求未知元素的过程.
在解直角三角形的过程中,一般要用到下面一些关系:
知识回顾
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
这节课我们来学习如何用已知的直角三角形两边来解直角三角形.
已知两边解直角三角形?
例1:如图,直角三角形ABC中,∠C=90°,a=4,c=8.解这个三角形.
A
C
B
解:在Rt △ABC中,
∵a ?+b ?=c ?,a=4,c=8.
∴b=
∵sinA=
∴ ∠A=30 °∠B=60 °
例2:
在直角三角形ABC中,∠C=90°,a=35,b=28.求∠A、∠B的度数和c的长.
解:在Rt△ABC中,
∵a?+b?=c?,a=35,b=28,
∴c=
∵tanA=
∴∠A≈51°
∠B=39°.
在图中的Rt△ABC中,根据AC=2.4,斜边AB=6,你能求出这个直角三角形的其他元素吗?
探究
能
A
B
C
α
6
2.4
如图,在Rt△ABC中,∠C=90°,
解这个直角三角形
解:
A
B
C
在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
a = 30 , b = 20 ;
解:根据勾股定理
A
B
C
b=20
a=30
c
???在△ABC中,∠C=90°,a=5,
求∠A、∠B、c边.
解:
∴∠A≈56.1°,
∴∠B=90°-56.1°=32.9°.
C
B
A
┓
a
b
c
解决有关比萨斜塔倾斜的问题.
设塔顶中心点为B,塔身中心线与垂直中心线的夹角为A,过B点向垂直中心线引垂线,垂足为点C(如图),在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m
所以∠A≈5°28′
A
B
C
A
B
C
已知两边,可先利用勾股定理求出第三边.然后再根据直角三角形的边角关系式求出所求角的三角函数值,从而求出所求角的角度,解直角三角形.
A
B
a
b
c
C
解直角三角形:
在直角三角形中,由已知元素求未知元素的过程.
在解直角三角形的过程中,一般要用到下面一些关系:
知识回顾
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
这节课我们来学习如何用已知的直角三角形两边来解直角三角形.
已知两边解直角三角形?
例1:如图,直角三角形ABC中,∠C=90°,a=4,c=8.解这个三角形.
A
C
B
解:在Rt △ABC中,
∵a ?+b ?=c ?,a=4,c=8.
∴b=
∵sinA=
∴ ∠A=30 °∠B=60 °
例2:
在直角三角形ABC中,∠C=90°,a=35,b=28.求∠A、∠B的度数和c的长.
解:在Rt△ABC中,
∵a?+b?=c?,a=35,b=28,
∴c=
∵tanA=
∴∠A≈51°
∠B=39°.
在图中的Rt△ABC中,根据AC=2.4,斜边AB=6,你能求出这个直角三角形的其他元素吗?
探究
能
A
B
C
α
6
2.4
如图,在Rt△ABC中,∠C=90°,
解这个直角三角形
解:
A
B
C
在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
a = 30 , b = 20 ;
解:根据勾股定理
A
B
C
b=20
a=30
c
???在△ABC中,∠C=90°,a=5,
求∠A、∠B、c边.
解:
∴∠A≈56.1°,
∴∠B=90°-56.1°=32.9°.
C
B
A
┓
a
b
c
解决有关比萨斜塔倾斜的问题.
设塔顶中心点为B,塔身中心线与垂直中心线的夹角为A,过B点向垂直中心线引垂线,垂足为点C(如图),在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m
所以∠A≈5°28′
A
B
C
A
B
C
已知两边,可先利用勾股定理求出第三边.然后再根据直角三角形的边角关系式求出所求角的三角函数值,从而求出所求角的角度,解直角三角形.
