4 解直角三角形 课件(13张PPT)
文档属性
| 名称 | 4 解直角三角形 课件(13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 903.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-12 09:01:41 | ||
图片预览


文档简介
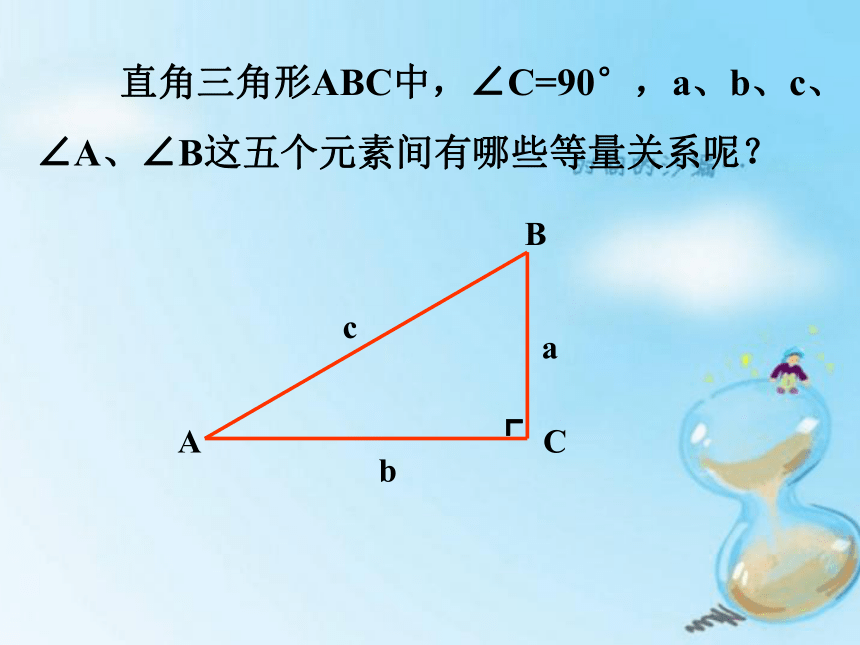
直角三角形ABC中,∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?
A
B
C
a
b
c
┓
5个
6个元素
三边
两个锐角
一个直角
(已知)
A
B
C
a
b
c
┓
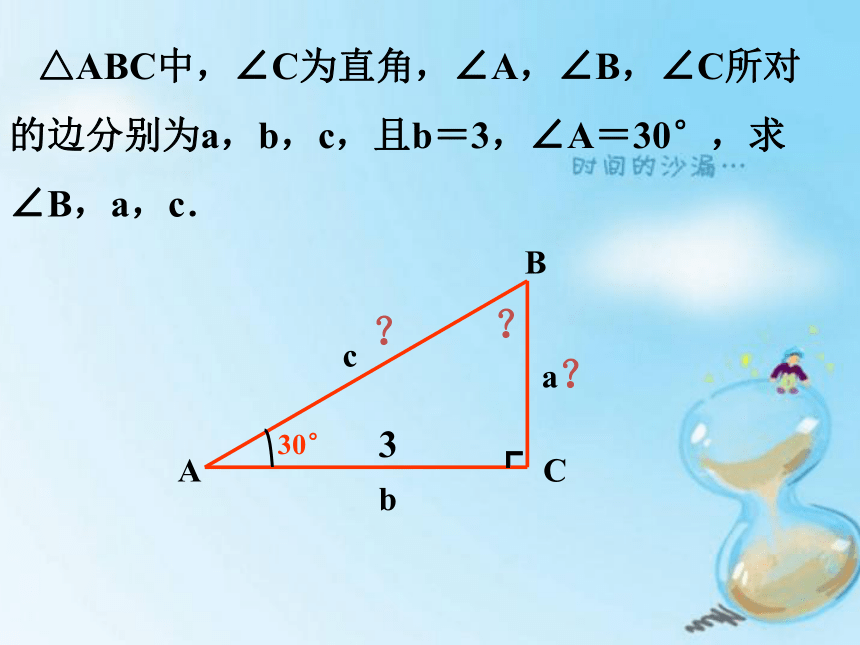
△ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且b=3,∠A=30°,求∠B,a,c.
A
B
C
a
b
c
3
30°
?
?
?
┓
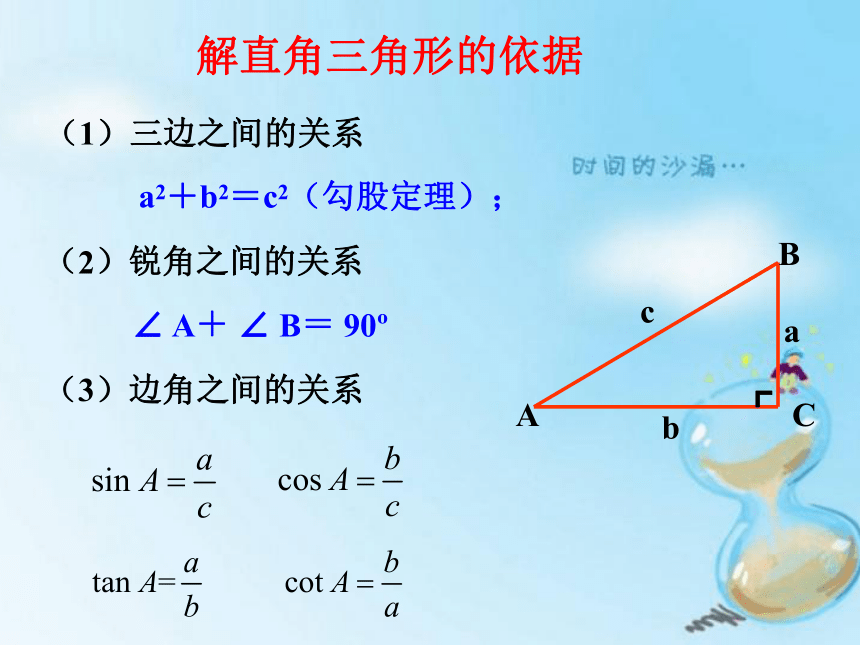
(1)三边之间的关系
a2+b2=c2(勾股定理);
(2)锐角之间的关系
∠ A+ ∠ B= 90?
(3)边角之间的关系
解直角三角形的依据
A
B
C
a
b
c
┓
A
C
B
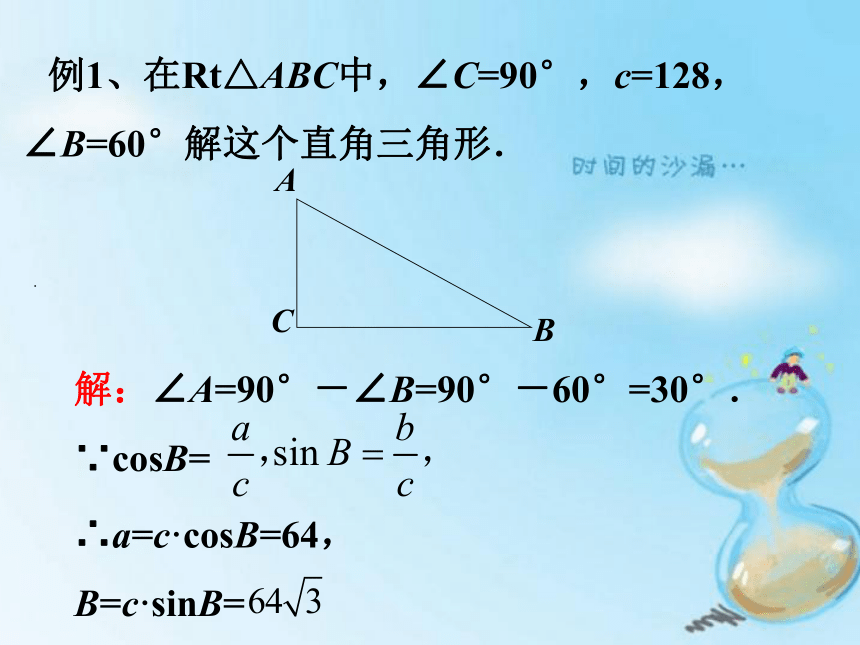
例1、在Rt△ABC中,∠C=90°,c=128,∠B=60°解这个直角三角形.
解:∠A=90°-∠B=90°-60°=30°.
∵cosB=
∴a=c·cosB=64,
B=c·sinB=
.
例2、在Rt△ABC中,∠C=90°,∠A=35°27′,a=15,解这个直角三角形.(精确到1)
解:∠B=90° - ∠A=54°33′.
∵tanB=
,sinA=
∴b=a·tanB≈21.
∴c=
??△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,
???? a=6,sinA= ,求b,c,tanA.
C
B
A
┓
a
b
c
在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,且c=287.4,∠B=42°6′,解这个三角形.
已知
两边
两直角边
一斜边,一直角边
一边一角
一锐角,一直角边
一锐角,一斜边
归纳
已知斜边求直边,正弦余弦很方便;
已知直边求直边,正切余切理当然;
已知两边求一角,函数关系要选好;
已知两边求一边,勾股定理最方便;
已知锐角求锐角,互余关系要记好;
已知直边求斜边,用除还需正余弦;
计算方法要选择,能用乘法不用除.
优选关系式
在△ABC中,∠C=90°,解这个直角三角形.
⑴∠A=60°,斜边上的高CD = ;
解:(1)∠B = 90°-∠A = 30°
AC=
练习
60°
A
B
C
D
┓
┓
这节课我们学到了什么?
A
B
C
a
b
c
┓
5个
6个元素
三边
两个锐角
一个直角
(已知)
A
B
C
a
b
c
┓
△ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且b=3,∠A=30°,求∠B,a,c.
A
B
C
a
b
c
3
30°
?
?
?
┓
(1)三边之间的关系
a2+b2=c2(勾股定理);
(2)锐角之间的关系
∠ A+ ∠ B= 90?
(3)边角之间的关系
解直角三角形的依据
A
B
C
a
b
c
┓
A
C
B
例1、在Rt△ABC中,∠C=90°,c=128,∠B=60°解这个直角三角形.
解:∠A=90°-∠B=90°-60°=30°.
∵cosB=
∴a=c·cosB=64,
B=c·sinB=
.
例2、在Rt△ABC中,∠C=90°,∠A=35°27′,a=15,解这个直角三角形.(精确到1)
解:∠B=90° - ∠A=54°33′.
∵tanB=
,sinA=
∴b=a·tanB≈21.
∴c=
??△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,
???? a=6,sinA= ,求b,c,tanA.
C
B
A
┓
a
b
c
在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,且c=287.4,∠B=42°6′,解这个三角形.
已知
两边
两直角边
一斜边,一直角边
一边一角
一锐角,一直角边
一锐角,一斜边
归纳
已知斜边求直边,正弦余弦很方便;
已知直边求直边,正切余切理当然;
已知两边求一角,函数关系要选好;
已知两边求一边,勾股定理最方便;
已知锐角求锐角,互余关系要记好;
已知直边求斜边,用除还需正余弦;
计算方法要选择,能用乘法不用除.
优选关系式
在△ABC中,∠C=90°,解这个直角三角形.
⑴∠A=60°,斜边上的高CD = ;
解:(1)∠B = 90°-∠A = 30°
AC=
练习
60°
A
B
C
D
┓
┓
这节课我们学到了什么?
