5 三角函数的应用 课件(16张)
图片预览





文档简介
解直角三角形
2 、tan10°·tan20°·tan30°·tan40°·tan50°
·tan60°·tan70°·tan80°=____________
3、若α是锐角,那么sinα+cosα的值为( )
A.大于1 B.等于1 C.小于1 D.不能确定
1 、在Rt△ABC中,∠C=90°,AB=4,BC=
则 = .
D
仰角、俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上向下看,视线与水平线的夹角叫做俯角
水平线
视线
视线
俯角
仰角
铅垂线
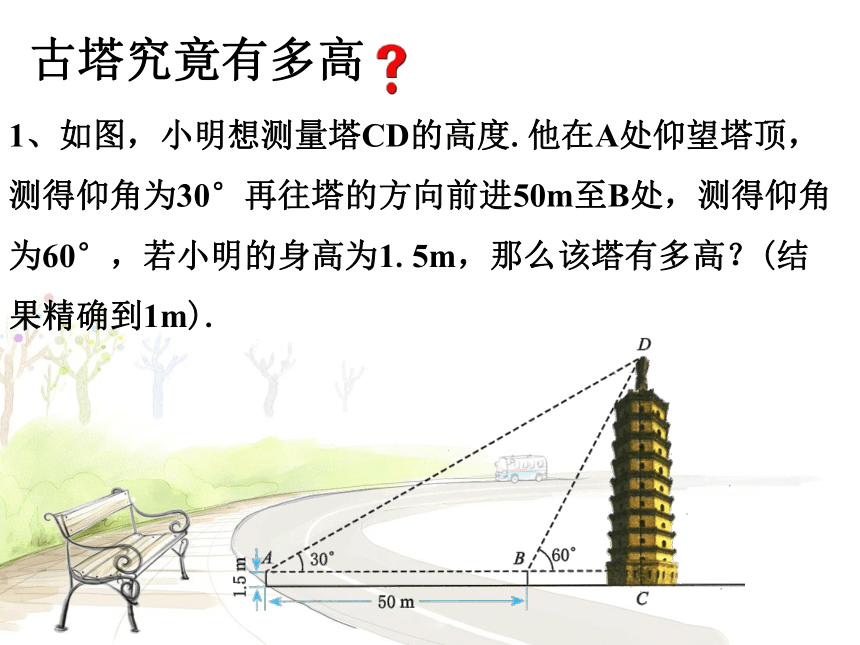
古塔究竟有多高
1、如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°再往塔的方向前进50m至B处,测得仰角为60°,若小明的身高为1.5m,那么该塔有多高?(结果精确到1m).
解:如图,根据题意知,∠A=30°,∠DBC=60°, AB=50m.
则∠ADC=60°,∠BDC=30°,∴∠BDA=30°
D
A
B
C
┌
50m
30°
60°
∴∠A=∠BDA
∴BD=AB=50
在Rt△DBC中,∠DBC=60°
sin60°=
∴DC=50×sin60°=
答:该塔约有43+1.5=44.5(m)高.
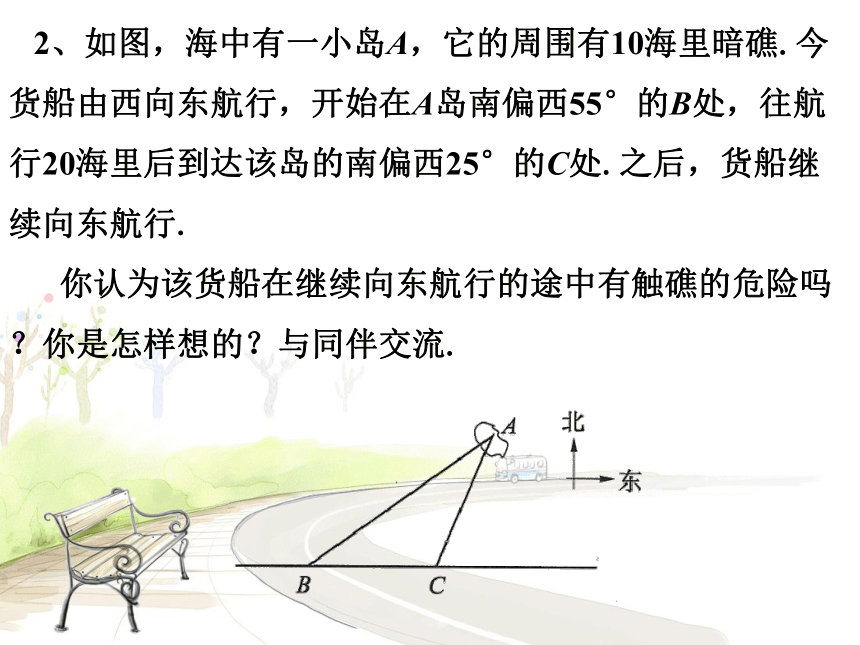
2、如图,海中有一小岛A,它的周围有10海里暗礁.今货船由西向东航行,开始在A岛南偏西55°的B处,往航行20海里后到达该岛的南偏西25°的C处.之后,货船继续向东航行.
你认为该货船在继续向东航行的途中有触礁的危险吗?你是怎样想的?与同伴交流.
A
D
C
B
25°
55°
20n mile
解:如图,可求出A到BC的最短距离即AD的长,若AD<10n mile,则有触礁危险,否则没有触礁危险.
设AD=x,由题意得:
解得x≈20.78n mile>10n mile
所以不会有触礁危险.
练习:1、2003年10月15日“神舟”5号载人航天飞船发射成功.当飞船完成变轨后,就在离地球表面350km的圆形轨道上运行,如图,当飞船运行到地球表面上P点的正上方时,从飞船上能直接看到地球上最远的点在什么位置?这样的最远点与P点的距离是多少?(地球半径约为6400km,Π取3.142,结果保留整数)
F
P
O
Q
2、热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与离楼的水平距离为120m,这栋高楼有我高?(结果保留小数后一位)
3、如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到过位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果保留小数点后一位)
A
P
B
C
A
B
D
C
4、在我市迎接奥运圣火的活动中,某校教学楼上悬挂着宣传条幅DC,小丽同学在点A处,测得条幅顶端D的仰角为30°,再向条幅方向前进10米后, 又在点B处测得条幅顶端D的仰角为45°,已知点A、B和C离地面高度都为1.44米,求条幅顶端D点距离地面的高度.
(计算结果精确到0.1米) 参考数据:
答案: 15.1米.
2.如图2,在离铁塔BE 120m的A处,用测角仪测量塔顶的仰角为30°,已知测角仪高AD=1.5m,则塔高BE= _________ (根号保留).
图1
图2
1.如图1,已知楼房AB高为50m,铁塔塔基距楼房地基间的水平距离BD为100m,塔高CD为 m,则下面结论中正确的是( )
A.由楼顶望塔顶仰角为60°
B.由楼顶望塔基俯角为60°
C.由楼顶望塔顶仰角为30°
D.由楼顶望塔基俯角为30°
C
A
B
C
D
D′
思考1:一架直升机从某塔顶A测得地面C、D两点的俯角分别为30°、 45°,若C、D与塔底B共线,CD=200米,求塔高AB?
思考2:有一块三形场地ABC,测得其中AB边长为60米,AC边长50米,∠ABC=30°,试求出这个三角形场地的面积.
简单实
际问题
数学模型
直角三角形
三角形
梯形
组合图形
构建
解
通过作高转化为直角三角形
解
数学建模及方程思想
解方程
1.把实际问题转化成数学问题,这个转化包括两个方面:一是将实际问题的图形转化为几何图形,画出正确的示意图;二是将已知条件转化为示意图中的边、角或它们之间的关系.
2.把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,画出直角三角形.
2 、tan10°·tan20°·tan30°·tan40°·tan50°
·tan60°·tan70°·tan80°=____________
3、若α是锐角,那么sinα+cosα的值为( )
A.大于1 B.等于1 C.小于1 D.不能确定
1 、在Rt△ABC中,∠C=90°,AB=4,BC=
则 = .
D
仰角、俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上向下看,视线与水平线的夹角叫做俯角
水平线
视线
视线
俯角
仰角
铅垂线
古塔究竟有多高
1、如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°再往塔的方向前进50m至B处,测得仰角为60°,若小明的身高为1.5m,那么该塔有多高?(结果精确到1m).
解:如图,根据题意知,∠A=30°,∠DBC=60°, AB=50m.
则∠ADC=60°,∠BDC=30°,∴∠BDA=30°
D
A
B
C
┌
50m
30°
60°
∴∠A=∠BDA
∴BD=AB=50
在Rt△DBC中,∠DBC=60°
sin60°=
∴DC=50×sin60°=
答:该塔约有43+1.5=44.5(m)高.
2、如图,海中有一小岛A,它的周围有10海里暗礁.今货船由西向东航行,开始在A岛南偏西55°的B处,往航行20海里后到达该岛的南偏西25°的C处.之后,货船继续向东航行.
你认为该货船在继续向东航行的途中有触礁的危险吗?你是怎样想的?与同伴交流.
A
D
C
B
25°
55°
20n mile
解:如图,可求出A到BC的最短距离即AD的长,若AD<10n mile,则有触礁危险,否则没有触礁危险.
设AD=x,由题意得:
解得x≈20.78n mile>10n mile
所以不会有触礁危险.
练习:1、2003年10月15日“神舟”5号载人航天飞船发射成功.当飞船完成变轨后,就在离地球表面350km的圆形轨道上运行,如图,当飞船运行到地球表面上P点的正上方时,从飞船上能直接看到地球上最远的点在什么位置?这样的最远点与P点的距离是多少?(地球半径约为6400km,Π取3.142,结果保留整数)
F
P
O
Q
2、热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与离楼的水平距离为120m,这栋高楼有我高?(结果保留小数后一位)
3、如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到过位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果保留小数点后一位)
A
P
B
C
A
B
D
C
4、在我市迎接奥运圣火的活动中,某校教学楼上悬挂着宣传条幅DC,小丽同学在点A处,测得条幅顶端D的仰角为30°,再向条幅方向前进10米后, 又在点B处测得条幅顶端D的仰角为45°,已知点A、B和C离地面高度都为1.44米,求条幅顶端D点距离地面的高度.
(计算结果精确到0.1米) 参考数据:
答案: 15.1米.
2.如图2,在离铁塔BE 120m的A处,用测角仪测量塔顶的仰角为30°,已知测角仪高AD=1.5m,则塔高BE= _________ (根号保留).
图1
图2
1.如图1,已知楼房AB高为50m,铁塔塔基距楼房地基间的水平距离BD为100m,塔高CD为 m,则下面结论中正确的是( )
A.由楼顶望塔顶仰角为60°
B.由楼顶望塔基俯角为60°
C.由楼顶望塔顶仰角为30°
D.由楼顶望塔基俯角为30°
C
A
B
C
D
D′
思考1:一架直升机从某塔顶A测得地面C、D两点的俯角分别为30°、 45°,若C、D与塔底B共线,CD=200米,求塔高AB?
思考2:有一块三形场地ABC,测得其中AB边长为60米,AC边长50米,∠ABC=30°,试求出这个三角形场地的面积.
简单实
际问题
数学模型
直角三角形
三角形
梯形
组合图形
构建
解
通过作高转化为直角三角形
解
数学建模及方程思想
解方程
1.把实际问题转化成数学问题,这个转化包括两个方面:一是将实际问题的图形转化为几何图形,画出正确的示意图;二是将已知条件转化为示意图中的边、角或它们之间的关系.
2.把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,画出直角三角形.
