6 二次函数的应用 课件(10张PPT)
文档属性
| 名称 | 6 二次函数的应用 课件(10张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 409.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-12 00:00:00 | ||
图片预览



文档简介
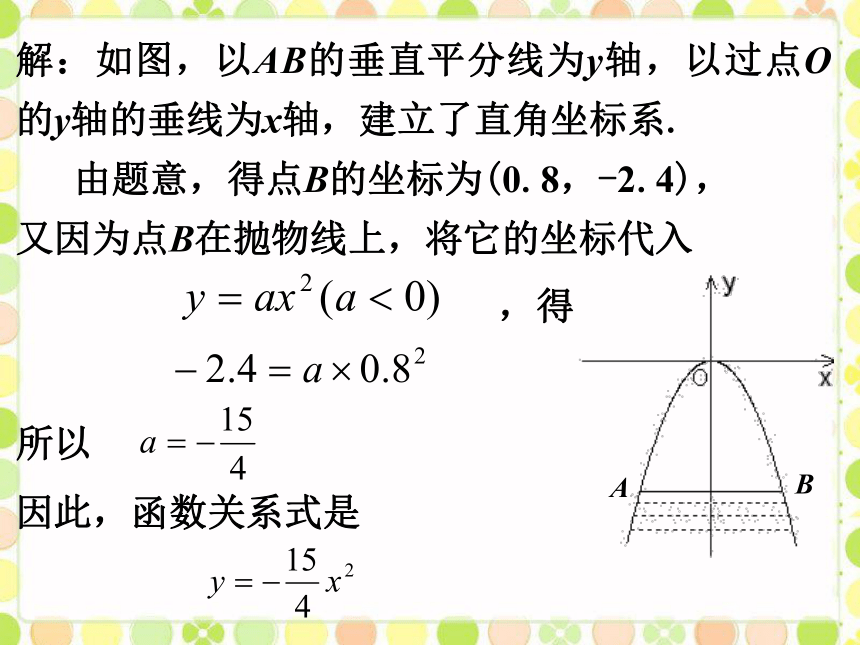
例1.某涵洞是抛物线形,它的截面如图所示,现测得水面宽1.6m,涵洞顶点O到水面的距离为2.4m,在图中直角坐标系内,涵洞所在的抛物线的函数关系式是什么?
分析:
如图,以AB的垂直平分线为y轴,以过点O的y轴的垂线为x轴,建立了直角坐标系.这时,涵洞所在的抛物线的顶点在原点,对称轴是y轴,开口向下,所以可设它的函数关系式是 .此时只需抛物线上的一个点就能求出抛物线的函数关系式.
A
B
解:如图,以AB的垂直平分线为y轴,以过点O的y轴的垂线为x轴,建立了直角坐标系.
由题意,得点B的坐标为(0.8,-2.4),
又因为点B在抛物线上,将它的坐标代入
,得
所以
因此,函数关系式是
B
A
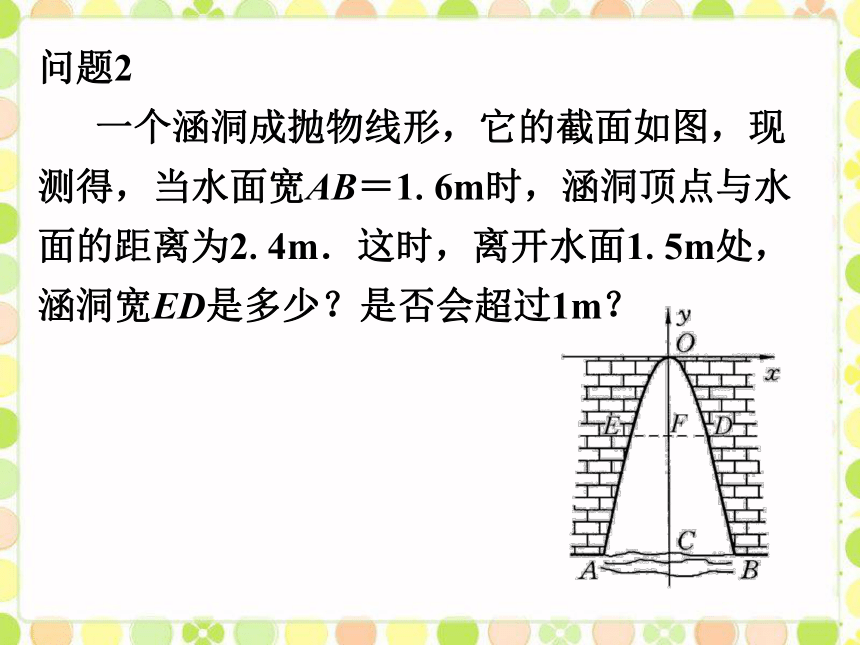
问题2
一个涵洞成抛物线形,它的截面如图,现测得,当水面宽AB=1.6m时,涵洞顶点与水面的距离为2.4m.这时,离开水面1.5m处,涵洞宽ED是多少?是否会超过1m?
例3 如图所示,公园要建造圆形喷水池.在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m.由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.
(1)如果不计其它因素,那么水池的半径至少要多少m,才能使喷出的水流不落到池外?
O
A
根据对称性,如果不计其它因素,
那么水池的半径至少要2.5m,才能使喷出的水流不致于落到池外.
解:(1)建立如图所示的坐标系,根据题意得,A点坐标为(0,1.25),顶点B坐标为(1,2.25).
当y=0时,可求得点C的坐标为(2.5,0)
同理,点D的坐标为(-2.5,0)
设抛物线为y=a(x-h)2+k,由待定系数法
可求得抛物线表达式为:y=-(x-1)2+2.25
x
y
O
A
●B(1,2.25)
●(0,1.25)
●
C(2.5,0)
●
D(-2.5,0)
如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线可以用 表示.(1)一辆货运卡车高4m,宽2m,它能通过该隧道吗?(2)如果该隧道内设双行道,那么这辆货运卡车是否可以通过?
(1)卡车可以通过.
提示:当x=±1时,y=3.75,
3.75+2>4.
(2)卡车可以通过.
提示:当x=±2时,y=3,3+2>4.
-1
-3
-1
-3
1
3
1
3
O
练习:1.有一抛物线拱桥,已知水位在AB位置时,水面的宽度是 m,水位上升4 m就达到警戒线CD,这时水面宽是 米.若洪水到来时,水位以每小时0.5m速度上升,求水过警戒线后几小时淹到拱桥顶端M处.
O
N
M
C
D
A
B
x
y
2.一场篮球赛中,球员甲跳起投篮,如图2,已知球在A处出手时离地面20/9 m,与篮筐中心C的水平距离是7m,当球运行的水平距离是4m时,达到最大高度4m(B处),设篮球运行的路线为抛物线.篮筐距地面3m. ①问此球能否投中?
②此时对方球员乙前来盖帽,已知乙跳起后摸到的最大高度为3.19m,他如何做才能盖帽成功?
分析:
如图,以AB的垂直平分线为y轴,以过点O的y轴的垂线为x轴,建立了直角坐标系.这时,涵洞所在的抛物线的顶点在原点,对称轴是y轴,开口向下,所以可设它的函数关系式是 .此时只需抛物线上的一个点就能求出抛物线的函数关系式.
A
B
解:如图,以AB的垂直平分线为y轴,以过点O的y轴的垂线为x轴,建立了直角坐标系.
由题意,得点B的坐标为(0.8,-2.4),
又因为点B在抛物线上,将它的坐标代入
,得
所以
因此,函数关系式是
B
A
问题2
一个涵洞成抛物线形,它的截面如图,现测得,当水面宽AB=1.6m时,涵洞顶点与水面的距离为2.4m.这时,离开水面1.5m处,涵洞宽ED是多少?是否会超过1m?
例3 如图所示,公园要建造圆形喷水池.在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m.由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.
(1)如果不计其它因素,那么水池的半径至少要多少m,才能使喷出的水流不落到池外?
O
A
根据对称性,如果不计其它因素,
那么水池的半径至少要2.5m,才能使喷出的水流不致于落到池外.
解:(1)建立如图所示的坐标系,根据题意得,A点坐标为(0,1.25),顶点B坐标为(1,2.25).
当y=0时,可求得点C的坐标为(2.5,0)
同理,点D的坐标为(-2.5,0)
设抛物线为y=a(x-h)2+k,由待定系数法
可求得抛物线表达式为:y=-(x-1)2+2.25
x
y
O
A
●B(1,2.25)
●(0,1.25)
●
C(2.5,0)
●
D(-2.5,0)
如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线可以用 表示.(1)一辆货运卡车高4m,宽2m,它能通过该隧道吗?(2)如果该隧道内设双行道,那么这辆货运卡车是否可以通过?
(1)卡车可以通过.
提示:当x=±1时,y=3.75,
3.75+2>4.
(2)卡车可以通过.
提示:当x=±2时,y=3,3+2>4.
-1
-3
-1
-3
1
3
1
3
O
练习:1.有一抛物线拱桥,已知水位在AB位置时,水面的宽度是 m,水位上升4 m就达到警戒线CD,这时水面宽是 米.若洪水到来时,水位以每小时0.5m速度上升,求水过警戒线后几小时淹到拱桥顶端M处.
O
N
M
C
D
A
B
x
y
2.一场篮球赛中,球员甲跳起投篮,如图2,已知球在A处出手时离地面20/9 m,与篮筐中心C的水平距离是7m,当球运行的水平距离是4m时,达到最大高度4m(B处),设篮球运行的路线为抛物线.篮筐距地面3m. ①问此球能否投中?
②此时对方球员乙前来盖帽,已知乙跳起后摸到的最大高度为3.19m,他如何做才能盖帽成功?
