1 对函数的再认识 课件(11张PPT)
文档属性
| 名称 | 1 对函数的再认识 课件(11张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 497.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-12 00:00:00 | ||
图片预览



文档简介
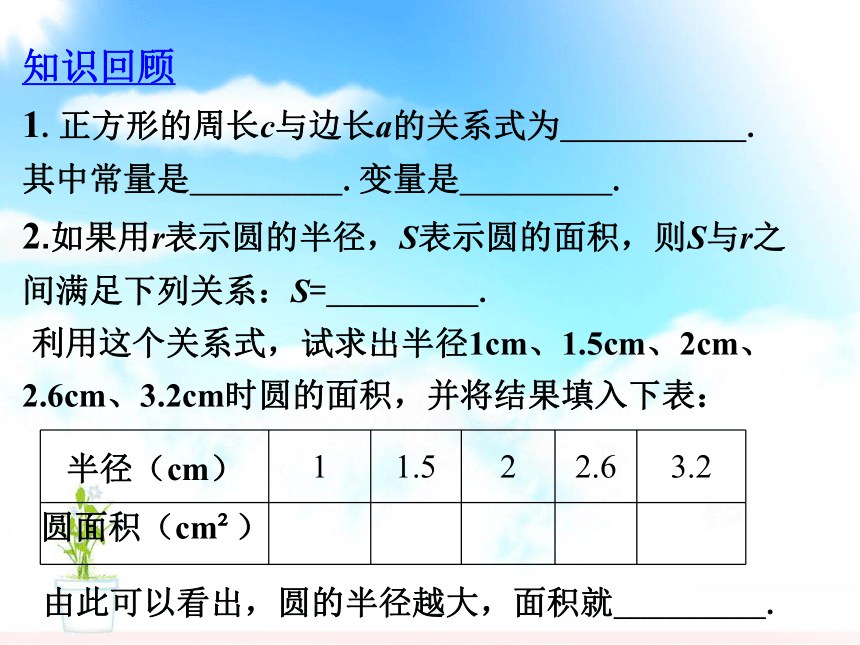
知识回顾
1.正方形的周长c与边长a的关系式为___________.
其中常量是_________.变量是_________.
2.如果用r表示圆的半径,S表示圆的面积,则S与r之间满足下列关系:S=_________.
利用这个关系式,试求出半径1cm、1.5cm、2cm、 2.6cm、3.2cm时圆的面积,并将结果填入下表:
半径(cm)
1
1.5
2
2.6
3.2
圆面积(cm?)
由此可以看出,圆的半径越大,面积就_________.
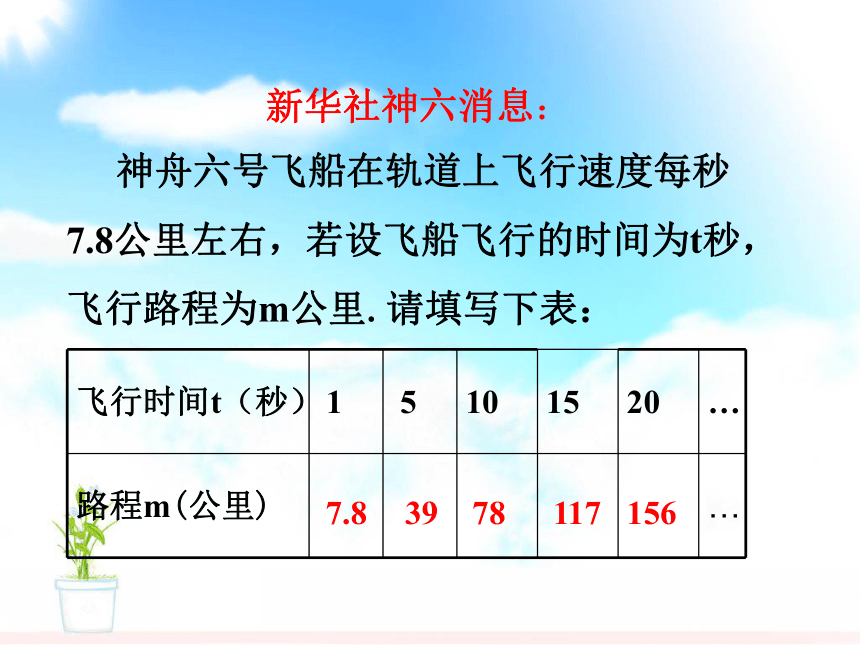
新华社神六消息:
神舟六号飞船在轨道上飞行速度每秒7.8公里左右,若设飞船飞行的时间为t秒,飞行路程为m公里.请填写下表:
飞行时间t(秒)
1
5
10
15
20
…
路程m(公里)
…
7.8
39
78
117
156
(1)在此次飞行过程中,当时间确定时,路程能确定吗?
(2) 你能用含t的代数式来表示m的值吗?
思考:
m=7.8t
在跳远比赛中,根据经验,跳远的距离是 ,( 是 助跑的速度,0< <10.5米/秒),其中变量 随着哪一个量的变化而变化?
一、创设情境,导入问题
1.小明的哥哥是一名大学生,他利用暑假去一家公司打工,报酬16元/时计算,设小明的哥哥这个月工作的时间为t时,应得报酬为m元.
怎样用关于 t 的代数式来表示m?
在以下问题中,哪些是变量?哪些是常量?
m = 16 t
二、自主探究,合作交流
上面各问题中两个变量 (t 与 m, s 与 v) 之间关系的有什么共同点吗?
m = 16 t
s = 0.085v2
三、尝试探索,揭示本质
一般地,在某个变化过程中,设有两个变量x,y,如果对于x的每一个确定的值,y都有唯一确定的值, 那么就说y是x的函数,x叫做自变量.
m是t的函数,t是自变量。
s是v的函数,v是自变量。
函数解析式
对于函数m=7.8t,当t=5时,能求得m的值吗?怎么求?
函数值:在这里,我们把m=39叫做当自变量t=5 时的函数值。
把它代入函数解析式,得
m=7.8t=7.8×5=39
请你思考
函数值概念
例:用总长为60m的篱笆围成矩形场地,求矩形面积s(m2)与一边长l(m)之间的关系式。并指出式中的常量与变量,并判断是否是函数关系式,若是,指出 自变量与函数。
说明:解决此类问题,关键是了解常量与变量,自变量与函数的意义。
典例剖析
1.每种商品的单价是每只5元,它的销售额y(元)与所授商品数量x(只)之间的关系式是( ),其中( )是( )的函数。
2.如图是某物体的抛射曲线图,其中s表示物体与抛射点之间的水平距离,h表示物体的高度.该图中的变量是( )与
( ),其中( )
是自变量( )的函数.
对应训练:
学习小结
1.你学到了哪些知识?要注意什么问题?
2.在学习的过程 中你有什么体会?
1.正方形的周长c与边长a的关系式为___________.
其中常量是_________.变量是_________.
2.如果用r表示圆的半径,S表示圆的面积,则S与r之间满足下列关系:S=_________.
利用这个关系式,试求出半径1cm、1.5cm、2cm、 2.6cm、3.2cm时圆的面积,并将结果填入下表:
半径(cm)
1
1.5
2
2.6
3.2
圆面积(cm?)
由此可以看出,圆的半径越大,面积就_________.
新华社神六消息:
神舟六号飞船在轨道上飞行速度每秒7.8公里左右,若设飞船飞行的时间为t秒,飞行路程为m公里.请填写下表:
飞行时间t(秒)
1
5
10
15
20
…
路程m(公里)
…
7.8
39
78
117
156
(1)在此次飞行过程中,当时间确定时,路程能确定吗?
(2) 你能用含t的代数式来表示m的值吗?
思考:
m=7.8t
在跳远比赛中,根据经验,跳远的距离是 ,( 是 助跑的速度,0< <10.5米/秒),其中变量 随着哪一个量的变化而变化?
一、创设情境,导入问题
1.小明的哥哥是一名大学生,他利用暑假去一家公司打工,报酬16元/时计算,设小明的哥哥这个月工作的时间为t时,应得报酬为m元.
怎样用关于 t 的代数式来表示m?
在以下问题中,哪些是变量?哪些是常量?
m = 16 t
二、自主探究,合作交流
上面各问题中两个变量 (t 与 m, s 与 v) 之间关系的有什么共同点吗?
m = 16 t
s = 0.085v2
三、尝试探索,揭示本质
一般地,在某个变化过程中,设有两个变量x,y,如果对于x的每一个确定的值,y都有唯一确定的值, 那么就说y是x的函数,x叫做自变量.
m是t的函数,t是自变量。
s是v的函数,v是自变量。
函数解析式
对于函数m=7.8t,当t=5时,能求得m的值吗?怎么求?
函数值:在这里,我们把m=39叫做当自变量t=5 时的函数值。
把它代入函数解析式,得
m=7.8t=7.8×5=39
请你思考
函数值概念
例:用总长为60m的篱笆围成矩形场地,求矩形面积s(m2)与一边长l(m)之间的关系式。并指出式中的常量与变量,并判断是否是函数关系式,若是,指出 自变量与函数。
说明:解决此类问题,关键是了解常量与变量,自变量与函数的意义。
典例剖析
1.每种商品的单价是每只5元,它的销售额y(元)与所授商品数量x(只)之间的关系式是( ),其中( )是( )的函数。
2.如图是某物体的抛射曲线图,其中s表示物体与抛射点之间的水平距离,h表示物体的高度.该图中的变量是( )与
( ),其中( )
是自变量( )的函数.
对应训练:
学习小结
1.你学到了哪些知识?要注意什么问题?
2.在学习的过程 中你有什么体会?
