5 三角函数的应用 课件(16张PPT)
图片预览



文档简介
图 (1)和(2)中,哪个山坡比较陡?
观察
(2)中的山坡比较陡.
(1)
(2)
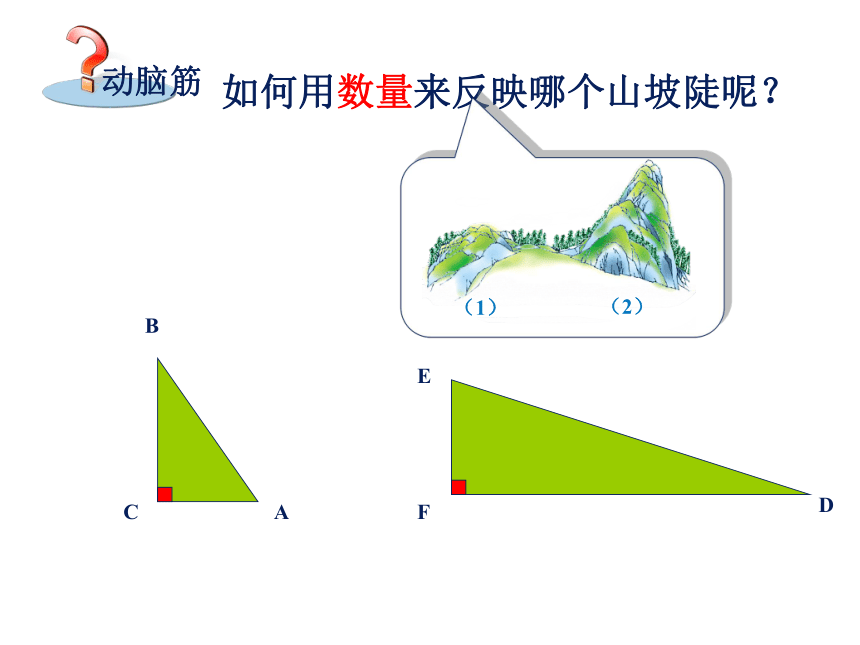
动脑筋
如何用数量来反映哪个山坡陡呢?
(1)
(2)
C
B
A
F
E
D
如图,从山坡脚下点P上坡走到点N 时,升高的高度h(即线段MN的长)与水平前进的距离l(即线段PM的长度)的比叫作坡度,用字母i表示,即
坡度通常写成 1 : m 的形式.
图中的∠MPN叫作坡角(即山坡与地平面的夹角).
显然,坡度等于坡角的正切.(即i=tanα)
坡度越大,山坡越陡.
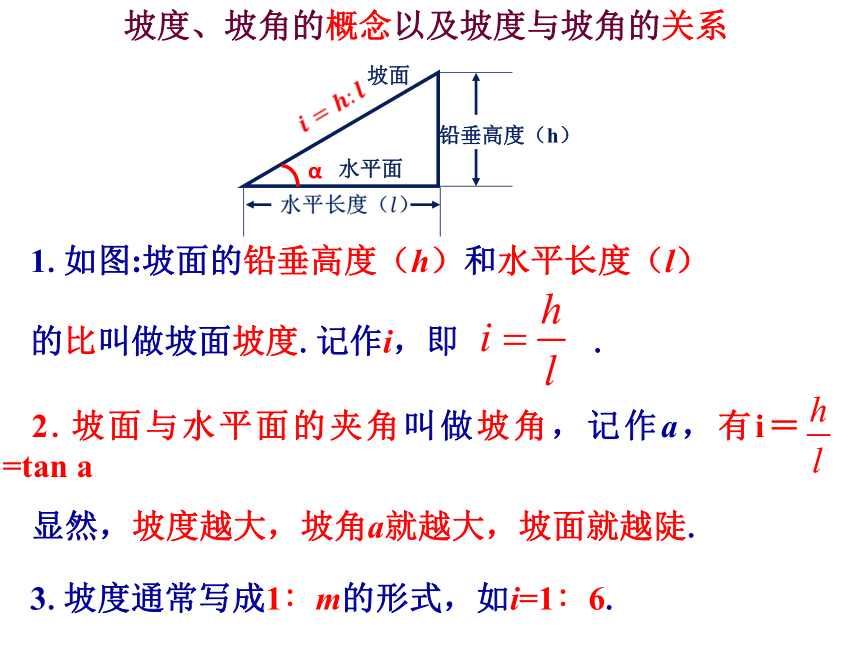
3.坡度通常写成1∶m的形式,如i=1∶6.
2.坡面与水平面的夹角叫做坡角,记作a,有i= =tan a
显然,坡度越大,坡角a就越大,坡面就越陡.
1.如图:坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面坡度.记作i,即 .
坡度、坡角的概念以及坡度与坡角的关系
铅垂高度(h)
α
坡面
水平面
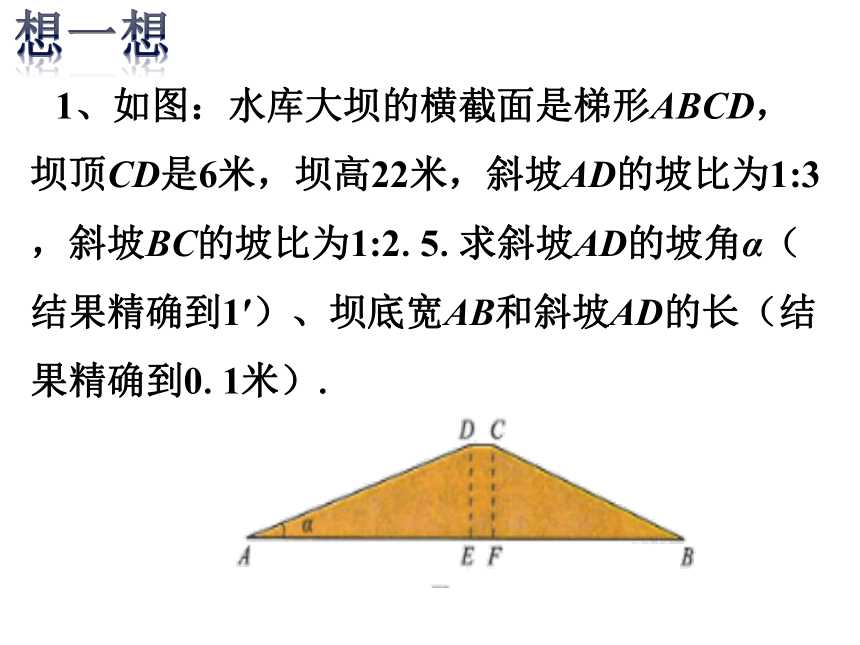
1、如图:水库大坝的横截面是梯形ABCD,坝顶CD是6米,坝高22米,斜坡AD的坡比为1:3,斜坡BC的坡比为1:2.5.求斜坡AD的坡角α(结果精确到1′)、坝底宽AB和斜坡AD的长(结果精确到0.1米).
解:由题可知 ,所以坡角α≈18°26′.
AD=
AE=18.0(m)
BF=
∴AB=AE+EF+BF=53.0(m)
A
α
F
E
D
C
B
2、如图:某校教学楼后面紧邻着一个山坡,坡上面是一块平地,BC∥AD,BE⊥AD,斜坡AB长26米,坡角∠BAD=68°.为了减缓坡面,防止山体滑坡,学校决定对该坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.
如果改造时,保持坡脚A不动,坡顶B沿BC左移11米到F点处,这样改造能确保山体不滑坡吗?
C
E
A
D
B
F
C
E
A
D
B
F
解:连接AF,过点F作FG垂直于AD于点G.则GE=BF=11m.
G
由题可求:FG=BE=AB·sin ∠BAD ≈24.1(m)
AE=AB·cos ∠BAD ≈9.7(m)
∴AG=AE+GE=20.7(m)∴tan ∠FAG ≈1.2
故∠FAG ≈49.3 ° <50 °
所以不会有滑坡危险.
1、如图, 一山坡的坡度 i = 1:1.8,小刚从山坡脚下点P上坡走了240m到达点N,他上升了多少米(精确到0.1m)?这座山坡的坡角是多少度(精确到1′)?
解:
用α表示坡角的大小,由于
因此α=29 °3 ′.
在直角三角形PMN中, ∠ P=29 °3 ′ PN=240m.
由于NM是∠P的对边,PN是斜边,
因此
从而
答:小刚上升了约116.5m,山坡的坡角约等于29°3′.
2、一物体沿坡度为1:8的山坡向上移动 米,则物体升高了_____米.
1
4、如上图,已知一商场自动扶梯的长l为13米,高度h为5米,自动扶梯与地面所成的夹角为θ,则tanθ的值为_____.
3、如下图,小明爬一土坡,他从A处爬到B处所走的直线距离AB=4米,此时,他离地面高度为h=2米,则这个土坡的坡角为_____.
30°
5、如图,在山坡上种植树时,要求株距(相邻两树间的水平距离)为5m.现测得斜坡的坡角为21°.求相邻两树间的坡面距离.(结果精确到0.1m)
解:由题意可知
∠BAC=18 °
在直角三角形ABC中,
所以A,B两点的距离约为5.4 m.
回顾与小结:
与同学交流,谈谈你在本节课中学到哪些知识?
1.坡度的定义;
3.坡角的定义;
4.坡度与坡角的关系;
2.坡度的表达形式;
观察
(2)中的山坡比较陡.
(1)
(2)
动脑筋
如何用数量来反映哪个山坡陡呢?
(1)
(2)
C
B
A
F
E
D
如图,从山坡脚下点P上坡走到点N 时,升高的高度h(即线段MN的长)与水平前进的距离l(即线段PM的长度)的比叫作坡度,用字母i表示,即
坡度通常写成 1 : m 的形式.
图中的∠MPN叫作坡角(即山坡与地平面的夹角).
显然,坡度等于坡角的正切.(即i=tanα)
坡度越大,山坡越陡.
3.坡度通常写成1∶m的形式,如i=1∶6.
2.坡面与水平面的夹角叫做坡角,记作a,有i= =tan a
显然,坡度越大,坡角a就越大,坡面就越陡.
1.如图:坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面坡度.记作i,即 .
坡度、坡角的概念以及坡度与坡角的关系
铅垂高度(h)
α
坡面
水平面
1、如图:水库大坝的横截面是梯形ABCD,坝顶CD是6米,坝高22米,斜坡AD的坡比为1:3,斜坡BC的坡比为1:2.5.求斜坡AD的坡角α(结果精确到1′)、坝底宽AB和斜坡AD的长(结果精确到0.1米).
解:由题可知 ,所以坡角α≈18°26′.
AD=
AE=18.0(m)
BF=
∴AB=AE+EF+BF=53.0(m)
A
α
F
E
D
C
B
2、如图:某校教学楼后面紧邻着一个山坡,坡上面是一块平地,BC∥AD,BE⊥AD,斜坡AB长26米,坡角∠BAD=68°.为了减缓坡面,防止山体滑坡,学校决定对该坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.
如果改造时,保持坡脚A不动,坡顶B沿BC左移11米到F点处,这样改造能确保山体不滑坡吗?
C
E
A
D
B
F
C
E
A
D
B
F
解:连接AF,过点F作FG垂直于AD于点G.则GE=BF=11m.
G
由题可求:FG=BE=AB·sin ∠BAD ≈24.1(m)
AE=AB·cos ∠BAD ≈9.7(m)
∴AG=AE+GE=20.7(m)∴tan ∠FAG ≈1.2
故∠FAG ≈49.3 ° <50 °
所以不会有滑坡危险.
1、如图, 一山坡的坡度 i = 1:1.8,小刚从山坡脚下点P上坡走了240m到达点N,他上升了多少米(精确到0.1m)?这座山坡的坡角是多少度(精确到1′)?
解:
用α表示坡角的大小,由于
因此α=29 °3 ′.
在直角三角形PMN中, ∠ P=29 °3 ′ PN=240m.
由于NM是∠P的对边,PN是斜边,
因此
从而
答:小刚上升了约116.5m,山坡的坡角约等于29°3′.
2、一物体沿坡度为1:8的山坡向上移动 米,则物体升高了_____米.
1
4、如上图,已知一商场自动扶梯的长l为13米,高度h为5米,自动扶梯与地面所成的夹角为θ,则tanθ的值为_____.
3、如下图,小明爬一土坡,他从A处爬到B处所走的直线距离AB=4米,此时,他离地面高度为h=2米,则这个土坡的坡角为_____.
30°
5、如图,在山坡上种植树时,要求株距(相邻两树间的水平距离)为5m.现测得斜坡的坡角为21°.求相邻两树间的坡面距离.(结果精确到0.1m)
解:由题意可知
∠BAC=18 °
在直角三角形ABC中,
所以A,B两点的距离约为5.4 m.
回顾与小结:
与同学交流,谈谈你在本节课中学到哪些知识?
1.坡度的定义;
3.坡角的定义;
4.坡度与坡角的关系;
2.坡度的表达形式;
