1 对函数的再认识 课件(10张PPT)
图片预览




文档简介
对函数的再认识
对于“函数”这个词我们并不陌生,大家还记得什么是函数吗?你能举出几个函数的例子吗?
你学过哪些函数?请你写出它们的表达式,它们的图象各是什么?
函数的定义是什么,你还记得吗?
复习回顾
一般的,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x 的函数,其中x是自变量,y是因变量.
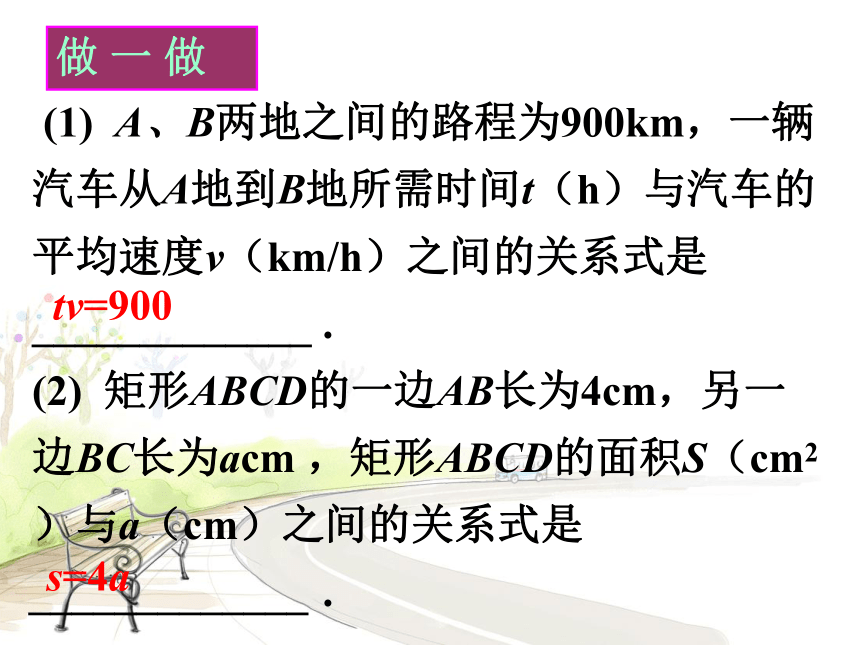
做 一 做
(1) A、B两地之间的路程为900km,一辆汽车从A地到B地所需时间t(h)与汽车的平均速度v(km/h)之间的关系式是_____________ .
(2) 矩形ABCD的一边AB长为4cm,另一边BC长为acm ,矩形ABCD的面积S(cm2)与a(cm)之间的关系式是_____________ .
tv=900
s=4a
(3)弹簧挂上物体后会伸长,测得一弹簧总长度y(cm)与所挂物体x(kg)之间有下面的关系:
x
0
1
2
3
4
5
6
y
1 2
12.5
1 3
13.5
1 4
14.5
1 5
若所挂物体质量为3kg,弹簧长度是_____.若所挂物体质量为6kg,弹簧长度是_____.若所挂物体质量为10kg,弹簧长度是_____.
13.5
15
17
在上面几个例子中 :
(1)自变量分别是什么 ? 自变量可以取值的范围是什么 ?
(2)对于自变量在它可以取值的范围内的每一个值,另一个变量是否都有惟一确定的值与它对应?
(3)由此你对函数有了哪些进一步的认识?与同伴进行交流.
函数
一般的,在一个变化过程中,有两个变量x和y,对于自变量x在某一范围内的每一个确定值,y都有惟一确定的值与它对应,那么我们称y是x 的函数,其中x是自变量,y是因变量.
问题探究
例1:
某种商品按进价提高30%后标价,又以9折优惠售出,试写出该商品每件的利润y(元)与每件的进价x(元)之间的关系式.
例题解析
y=1.3*0.9x-x
例2:
当x =3时, 求各函数y的对应值 :
(1)y=3x+7; (2)y=-2x2-1 ;
(3)y= ; (4)y=
例题解析
对于自变量 x 在可以取值范围内的一个确定的值α, 函数y有惟一确定的对应值 , 这个对应值叫做_______ .
如对于例 2(1) 中的函数y=3x+7,16就是当x =3 时的函数值 .
问题与思考
函数值
对于“函数”这个词我们并不陌生,大家还记得什么是函数吗?你能举出几个函数的例子吗?
你学过哪些函数?请你写出它们的表达式,它们的图象各是什么?
函数的定义是什么,你还记得吗?
复习回顾
一般的,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x 的函数,其中x是自变量,y是因变量.
做 一 做
(1) A、B两地之间的路程为900km,一辆汽车从A地到B地所需时间t(h)与汽车的平均速度v(km/h)之间的关系式是_____________ .
(2) 矩形ABCD的一边AB长为4cm,另一边BC长为acm ,矩形ABCD的面积S(cm2)与a(cm)之间的关系式是_____________ .
tv=900
s=4a
(3)弹簧挂上物体后会伸长,测得一弹簧总长度y(cm)与所挂物体x(kg)之间有下面的关系:
x
0
1
2
3
4
5
6
y
1 2
12.5
1 3
13.5
1 4
14.5
1 5
若所挂物体质量为3kg,弹簧长度是_____.若所挂物体质量为6kg,弹簧长度是_____.若所挂物体质量为10kg,弹簧长度是_____.
13.5
15
17
在上面几个例子中 :
(1)自变量分别是什么 ? 自变量可以取值的范围是什么 ?
(2)对于自变量在它可以取值的范围内的每一个值,另一个变量是否都有惟一确定的值与它对应?
(3)由此你对函数有了哪些进一步的认识?与同伴进行交流.
函数
一般的,在一个变化过程中,有两个变量x和y,对于自变量x在某一范围内的每一个确定值,y都有惟一确定的值与它对应,那么我们称y是x 的函数,其中x是自变量,y是因变量.
问题探究
例1:
某种商品按进价提高30%后标价,又以9折优惠售出,试写出该商品每件的利润y(元)与每件的进价x(元)之间的关系式.
例题解析
y=1.3*0.9x-x
例2:
当x =3时, 求各函数y的对应值 :
(1)y=3x+7; (2)y=-2x2-1 ;
(3)y= ; (4)y=
例题解析
对于自变量 x 在可以取值范围内的一个确定的值α, 函数y有惟一确定的对应值 , 这个对应值叫做_______ .
如对于例 2(1) 中的函数y=3x+7,16就是当x =3 时的函数值 .
问题与思考
函数值
