2.1平面向量的实际背景及基本概念(共26张PPT)
文档属性
| 名称 | 2.1平面向量的实际背景及基本概念(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-12 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
问题提出
1.在物理中,位移与距离是同一个概念吗?为什么?
2.现实世界中有各种各样的量,如年龄、身高、体重、力、速度、面积、体积、温度等,在数学上,为了正确理解、区分这些量,我们引进一个新的概念.
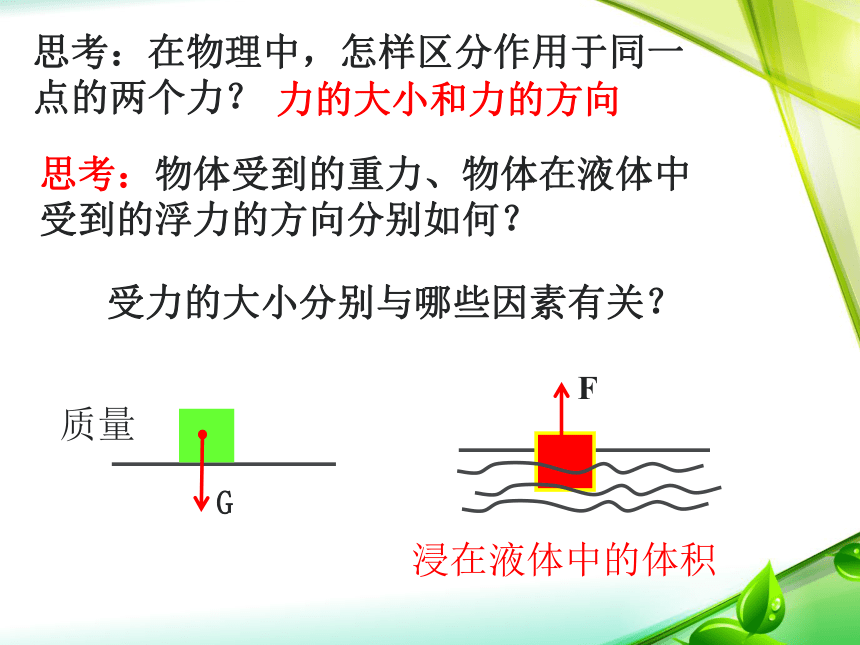
思考:在物理中,怎样区分作用于同一点的两个力?
力的大小和力的方向
思考:物体受到的重力、物体在液体中受到的浮力的方向分别如何?
质量
浸在液体中的体积
受力的大小分别与哪些因素有关?
思考:在如图所示的弹簧中,被拉长或压缩的弹簧的弹力方向如何?在弹性限度内,弹力的大小与什么因素有关?
弹簧拉长或压缩的长度
重力,浮力,弹力都有一个共同的特点:
既有方向,又有大小。
那么数学中,我们把既有大小,又有方向的量叫做什么?.只有大小,没有方向的量又称为什么?
物理中,我们把既有大小,又有方向的量叫做矢量.只有大小,没有方向的量称为标量。
2.1
平面向量的实际背景及基本概念
【与向量有关的概念】
向量----数学中,把既有大小,又有方向的量叫
做向量.
数量----把只有大小,没有方向的量称为数量。
思考:年龄、身高、长度、面积、体积、温度、
时间、路程、质量等是向量吗?
向量与数量有什么区别?
区别:向量有方向且不能比较大小,
数量无方向且能比较大小.
有向线段:在线段AB的两个端点中,规定一个顺序,假设A为起点,B为终点,我们就说线段AB具有方向.具有方向的线段叫做有向线段.
有向线段的三个要素:起点、方向、长度.
B(终点)
A(起点)
向量如何表示?
①几何表示——向量常用有向线段表示:有向线段的长度表示向量的大小,箭头所指的方向表示向量的方向。
练习:1.温度有零上和零下之分,温度是向量吗?为什么?
我们所说的向量,与起点无关,用有向线段表示向量时,起点可以取任意位置。所以数学中的向量也叫自由向量.
如图:他们都表示同一个向量。
不是,温度只有大小,没有方向。
不是,方向不同
说明:
长度等于1个单位的向量,叫做单位向量.
【零向量】
规定:零向量0的方向是任意的.
注意:零向量0与实数0的含义、书写区别.
注:零向量,单位向量都是只限制大小,不确定方向的.
思考:在平面直角坐标系中,起点在原点的所有单位向量,它们的终点的集合组成的是什么图形?
一个以o为圆心,单位长度为半径的圆。
1.把平面上所有方向相同的向量的起点平行移动到同一点O,那么这些向量的终点所构成的图形是( )
A.一条线段
B.一条直线
C.一条射线
D.一个点
C
指出图中各向量的长度.
(课本P77
3)
②.向量的字母表示:
普通字体:a,
b,
c,
d,
e
粗黑体字:a,
b,
c,
d,
e
注意:印刷版常用(粗)黑体字表示向量:
思考:因为向量完全由它的方向和模确定.对于两个非零向量a、b,就其模等与不等,方向同与不同而言,有哪几种可能情形?
模相等,
方向不相同;
模不相等,
方向相同;
模不相等,
方向不相同;
模相等,
方向相同;
【平行向量】
①方向相同或相反的非零向量叫平行向量
如图:用有向线段表示的两个平行向量a、b.
向量a、b平行,记作
a
∥b
【平行向量】
②规定:零向量与任一向量平行.
即对于任意向量a,都有
0∥a
(2)向量a、b、c平行,如左图
记作a∥b∥c.
练习.判断下列各组向量是否平行?
①
④
③
②
向量的平行与线段的平行有什么区别?
平行向量又叫做共线向量
将向量平移,不会改变其长度和方向.
2.四边形ABCD中,
则四边形ABCD( )
A.是平行四边形
B.是梯形
C.是平行四边形或梯形
D.不是平行四边形,也不是梯形
C
向量相等
向量平行
平行向量一定是相等向量吗?
长度相等且方向相同的向量叫做相等向量.
相等向量一定是平行向量吗?
11个
练习:课本
P77A组
3
4.(1)用有向线段表示两个相等的向量,如果有相同的起点,那么它们的终点是否相同?
4.(2)用有向线段表示两个共线向量,如果有相同的起点,那么它们的终点是否相同?
课本77页练习
请判断下列说法的对错:
(1)
单位向量都相等;
(2)
长度不等且方向相反的两向量不一定共线;
×
×
×
√
×
×
问题提出
1.在物理中,位移与距离是同一个概念吗?为什么?
2.现实世界中有各种各样的量,如年龄、身高、体重、力、速度、面积、体积、温度等,在数学上,为了正确理解、区分这些量,我们引进一个新的概念.
思考:在物理中,怎样区分作用于同一点的两个力?
力的大小和力的方向
思考:物体受到的重力、物体在液体中受到的浮力的方向分别如何?
质量
浸在液体中的体积
受力的大小分别与哪些因素有关?
思考:在如图所示的弹簧中,被拉长或压缩的弹簧的弹力方向如何?在弹性限度内,弹力的大小与什么因素有关?
弹簧拉长或压缩的长度
重力,浮力,弹力都有一个共同的特点:
既有方向,又有大小。
那么数学中,我们把既有大小,又有方向的量叫做什么?.只有大小,没有方向的量又称为什么?
物理中,我们把既有大小,又有方向的量叫做矢量.只有大小,没有方向的量称为标量。
2.1
平面向量的实际背景及基本概念
【与向量有关的概念】
向量----数学中,把既有大小,又有方向的量叫
做向量.
数量----把只有大小,没有方向的量称为数量。
思考:年龄、身高、长度、面积、体积、温度、
时间、路程、质量等是向量吗?
向量与数量有什么区别?
区别:向量有方向且不能比较大小,
数量无方向且能比较大小.
有向线段:在线段AB的两个端点中,规定一个顺序,假设A为起点,B为终点,我们就说线段AB具有方向.具有方向的线段叫做有向线段.
有向线段的三个要素:起点、方向、长度.
B(终点)
A(起点)
向量如何表示?
①几何表示——向量常用有向线段表示:有向线段的长度表示向量的大小,箭头所指的方向表示向量的方向。
练习:1.温度有零上和零下之分,温度是向量吗?为什么?
我们所说的向量,与起点无关,用有向线段表示向量时,起点可以取任意位置。所以数学中的向量也叫自由向量.
如图:他们都表示同一个向量。
不是,温度只有大小,没有方向。
不是,方向不同
说明:
长度等于1个单位的向量,叫做单位向量.
【零向量】
规定:零向量0的方向是任意的.
注意:零向量0与实数0的含义、书写区别.
注:零向量,单位向量都是只限制大小,不确定方向的.
思考:在平面直角坐标系中,起点在原点的所有单位向量,它们的终点的集合组成的是什么图形?
一个以o为圆心,单位长度为半径的圆。
1.把平面上所有方向相同的向量的起点平行移动到同一点O,那么这些向量的终点所构成的图形是( )
A.一条线段
B.一条直线
C.一条射线
D.一个点
C
指出图中各向量的长度.
(课本P77
3)
②.向量的字母表示:
普通字体:a,
b,
c,
d,
e
粗黑体字:a,
b,
c,
d,
e
注意:印刷版常用(粗)黑体字表示向量:
思考:因为向量完全由它的方向和模确定.对于两个非零向量a、b,就其模等与不等,方向同与不同而言,有哪几种可能情形?
模相等,
方向不相同;
模不相等,
方向相同;
模不相等,
方向不相同;
模相等,
方向相同;
【平行向量】
①方向相同或相反的非零向量叫平行向量
如图:用有向线段表示的两个平行向量a、b.
向量a、b平行,记作
a
∥b
【平行向量】
②规定:零向量与任一向量平行.
即对于任意向量a,都有
0∥a
(2)向量a、b、c平行,如左图
记作a∥b∥c.
练习.判断下列各组向量是否平行?
①
④
③
②
向量的平行与线段的平行有什么区别?
平行向量又叫做共线向量
将向量平移,不会改变其长度和方向.
2.四边形ABCD中,
则四边形ABCD( )
A.是平行四边形
B.是梯形
C.是平行四边形或梯形
D.不是平行四边形,也不是梯形
C
向量相等
向量平行
平行向量一定是相等向量吗?
长度相等且方向相同的向量叫做相等向量.
相等向量一定是平行向量吗?
11个
练习:课本
P77A组
3
4.(1)用有向线段表示两个相等的向量,如果有相同的起点,那么它们的终点是否相同?
4.(2)用有向线段表示两个共线向量,如果有相同的起点,那么它们的终点是否相同?
课本77页练习
请判断下列说法的对错:
(1)
单位向量都相等;
(2)
长度不等且方向相反的两向量不一定共线;
×
×
×
√
×
×
