1.5 利用三角形的全等测距离同步练习题(含答案)
文档属性
| 名称 | 1.5 利用三角形的全等测距离同步练习题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-13 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第一章 三角形
5 利用三角形的全等测距离
夯实基础
知识点 利用三角形全等测距离
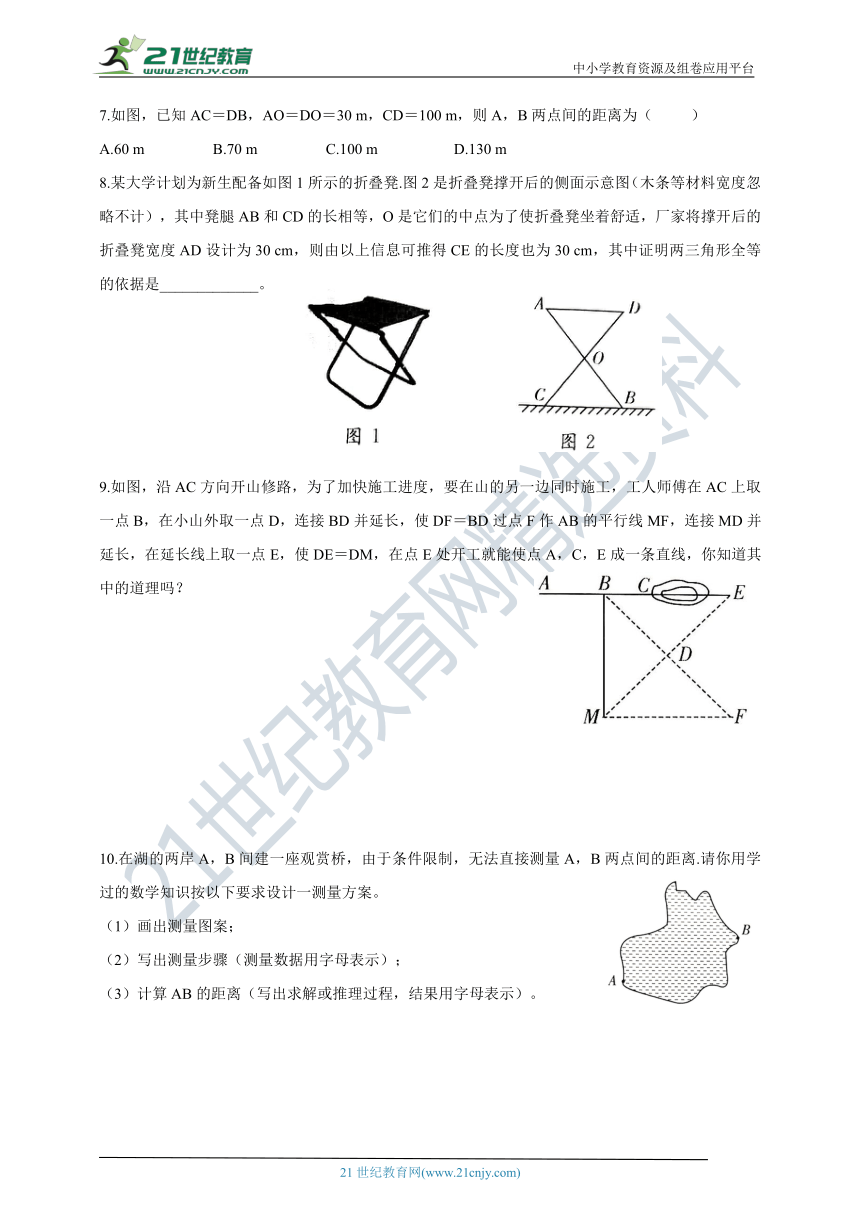
1.在新修的花园小区中,有一条“Z”字形绿色长瓶ABCD(如图),其中AB∥CD,在AB,BC,CD三段绿色长廊上各修建一凉亭E,M,F,且BE=CF,M是BC的中点,E,M,F在一条直线上若在凉M与F之间有一池塘,不能直接到达,塑想知道M与F之间的距离,要测出的长度是( )
A. EM B. BE C.CF D.CM
2.在一次小制作活动中,艳艳剪了一个燕尾图案(如图),她用刻度尺量得AB=AD,BC=DC,又准备用量角器量∠B和∠D是否相等,小亮走过来说:“不用量了,肯定相等”,小亮依据的是全等三角形的性质及判定三角形全等的( )
A. ASA B. SSS C. SAS D. AAS
3.教室里有几盆花,如图①所示,因为测量这几盆花两旁的A,B两点间的距离不方便,因此,选点A,B都能到达的一点O,如图②所示,连接BO并延长BO到点C,使CO=BO,连接AO并延长AO到点D,使DO=AO.那么C,D两点间的距离就是A,B两点间的距离。
理由:在△COD和△BOA中,因为所以△COD≌△BOA( ).
所以CD=_________________。
所以只要测出C,D两点间的距离就可知A,B两点间的距离。
4.杨阳同学沿一段笔直的人行道行走,在由A处步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等A,BD相交于点O,OD⊥CD,垂足为点D.已知AB=20m.请根据上述信息求标语CD的长度.
易错点 混淆判定三角形全等的条件,导致判定依据不正确
5.如图,由两根钢丝固定的高压电线杆,按要求当两根钢丝与电线杆的夹角相同时,固定效果最好.现已知钢丝触地点到电线杆的距离相等,那么请你判断图中两根钢丝的固定是否符合要求,并说明理由.(电线杆的粗细忽略不计)
能力提升
6.如图,有两个长度相同的滑梯靠在一面墙上已知AC=DF,AB=DE,则这两个滑梯与地面夹角
∠ABC与∠DFE的度数和是( )
A.60° B.90° C.120° D.150°
7.如图,已知AC=DB,AO=DO=30 m,CD=100 m,则A,B两点间的距离为( )
A.60 m B.70 m C.100 m D.130 m
8.某大学计划为新生配备如图1所示的折叠凳.图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30 cm,则由以上信息可推得CE的长度也为30 cm,其中证明两三角形全等的依据是_____________。
9.如图,沿AC方向开山修路,为了加快施工进度,要在山的另一边同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD并延长,使DF=BD过点F作AB的平行线MF,连接MD并延长,在延长线上取一点E,使DE=DM,在点E处开工就能使点A,C,E成一条直线,你知道其中的道理吗?
10.在湖的两岸A,B间建一座观赏桥,由于条件限制,无法直接测量A,B两点间的距离.请你用学过的数学知识按以下要求设计一测量方案。
(1)画出测量图案;
(2)写出测量步骤(测量数据用字母表示);
(3)计算AB的距离(写出求解或推理过程,结果用字母表示)。
素养提升
11.如图,在△ABC中,D为AB的中点,AD=5 cm,∠B=∠C,BC=8 cm。
(1)若点P在线段BC上以3cm/s的速度从点B向终点C运动,同时点Q在线段CA上从点C向终点A运动。
①若点Q的速度与点P的速度相等,经过1 s后,请说明△BPD≌△CQP;
②若点Q的速度与点P的速度不等,当点Q的速度为多少时,能使△BPD≌△CPQ?
(2)若点P以3 cm/s的速度从点B向点C运动,同时点Q以5 cm/s的速度从点C向点A运动,它们都依次沿△ABC三边运动,则经过多长时间,点Q第一次在△ABC的哪条边上追上点P?
参考答案
1. A 2. B 3. SAS AB
4.解:因为AB∥CD,所以∠ABO=∠CDO.
又因为OD⊥CD,所以∠CDO=90°
所以∠ABO=90°,即BO⊥AB
因为AB∥OH∥CD(相邻两平行线间的距离相等),所以OB=OD.
在△ABO和△CDO中,因为∠ABO=∠CDO,OB=OD,∠AOB=∠COD,
所以△ABO≌△CDO(ASA)所以AB=CD=20m.
即标语CD的长度为20m.
5.解:两根钢丝的固定符合要求。
理由:由题意可知AO⊥BC,OB=OC,所以∠AOB=∠AOC=90°
在△AOB和△AOC中,因为所以△AOB≌△AOC(SAS),
所以∠BAO=∠CAO.故两根钢丝的固定符合要求。
6.B
7.C 【解析】因为AC=DB,AO=DO,所以OB=OC.又因为∠AOB=∠DOC,所以△AOB≌△DOC.所以AB=CD=100 m。
8. SAS
9.解:在△BDE和△FDM中,因为所以△BDE≌△FDM(SAS).
所以∠BED=∠FMD,即∠BEM=∠FME,所以BE∥MF,
因为AB∥MF,所以A,C,E三点在一条直线上。
10.解:(1)如图所示.
(2)在湖岸上选一点O,连接BO并延长到点C,使BO=OC,连接AO并延长到点D,使OD=AO,连接CD,则AB=CD.测量DC的长度即为AB的长度.
(3)设CD=m.
因为BO=CO,∠AOB=∠COD,AO=DO,所以△AOB≌△DOC(SAS)
所以AB=CD=m.
11.解:(1)①因为BP=3×1=3,CQ=3×1=3,所以BP=CQ.
因为D为AB的中点,所以BD=AD=5.
因为CP=BC-BP=5,所以BD=CP.
在△BPD和△CQP中,因为所以△BPD≌△CQP
②设点Q运动时间为t s,运动速度为v cm/s
因为△BPD≌△CPQ,所以BP=CP=4,CQ=5.
所以,所以。
即当点Q的速度为cm/s时,能使△BPD≌△CPQ。
(2)设经过x秒后,点Q第一次追上点P,
由题意得5x-3x=2×10,解得x=10.
所以点P运动的路程为3×10=30.
因为30=28+2,
所以此时点P在BC边上,
所以经过10 s,点Q第一次在△ABC的BC边上追上点P.
_21?????????è?????(www.21cnjy.com)_
第一章 三角形
5 利用三角形的全等测距离
夯实基础
知识点 利用三角形全等测距离
1.在新修的花园小区中,有一条“Z”字形绿色长瓶ABCD(如图),其中AB∥CD,在AB,BC,CD三段绿色长廊上各修建一凉亭E,M,F,且BE=CF,M是BC的中点,E,M,F在一条直线上若在凉M与F之间有一池塘,不能直接到达,塑想知道M与F之间的距离,要测出的长度是( )
A. EM B. BE C.CF D.CM
2.在一次小制作活动中,艳艳剪了一个燕尾图案(如图),她用刻度尺量得AB=AD,BC=DC,又准备用量角器量∠B和∠D是否相等,小亮走过来说:“不用量了,肯定相等”,小亮依据的是全等三角形的性质及判定三角形全等的( )
A. ASA B. SSS C. SAS D. AAS
3.教室里有几盆花,如图①所示,因为测量这几盆花两旁的A,B两点间的距离不方便,因此,选点A,B都能到达的一点O,如图②所示,连接BO并延长BO到点C,使CO=BO,连接AO并延长AO到点D,使DO=AO.那么C,D两点间的距离就是A,B两点间的距离。
理由:在△COD和△BOA中,因为所以△COD≌△BOA( ).
所以CD=_________________。
所以只要测出C,D两点间的距离就可知A,B两点间的距离。
4.杨阳同学沿一段笔直的人行道行走,在由A处步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等A,BD相交于点O,OD⊥CD,垂足为点D.已知AB=20m.请根据上述信息求标语CD的长度.
易错点 混淆判定三角形全等的条件,导致判定依据不正确
5.如图,由两根钢丝固定的高压电线杆,按要求当两根钢丝与电线杆的夹角相同时,固定效果最好.现已知钢丝触地点到电线杆的距离相等,那么请你判断图中两根钢丝的固定是否符合要求,并说明理由.(电线杆的粗细忽略不计)
能力提升
6.如图,有两个长度相同的滑梯靠在一面墙上已知AC=DF,AB=DE,则这两个滑梯与地面夹角
∠ABC与∠DFE的度数和是( )
A.60° B.90° C.120° D.150°
7.如图,已知AC=DB,AO=DO=30 m,CD=100 m,则A,B两点间的距离为( )
A.60 m B.70 m C.100 m D.130 m
8.某大学计划为新生配备如图1所示的折叠凳.图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30 cm,则由以上信息可推得CE的长度也为30 cm,其中证明两三角形全等的依据是_____________。
9.如图,沿AC方向开山修路,为了加快施工进度,要在山的另一边同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD并延长,使DF=BD过点F作AB的平行线MF,连接MD并延长,在延长线上取一点E,使DE=DM,在点E处开工就能使点A,C,E成一条直线,你知道其中的道理吗?
10.在湖的两岸A,B间建一座观赏桥,由于条件限制,无法直接测量A,B两点间的距离.请你用学过的数学知识按以下要求设计一测量方案。
(1)画出测量图案;
(2)写出测量步骤(测量数据用字母表示);
(3)计算AB的距离(写出求解或推理过程,结果用字母表示)。
素养提升
11.如图,在△ABC中,D为AB的中点,AD=5 cm,∠B=∠C,BC=8 cm。
(1)若点P在线段BC上以3cm/s的速度从点B向终点C运动,同时点Q在线段CA上从点C向终点A运动。
①若点Q的速度与点P的速度相等,经过1 s后,请说明△BPD≌△CQP;
②若点Q的速度与点P的速度不等,当点Q的速度为多少时,能使△BPD≌△CPQ?
(2)若点P以3 cm/s的速度从点B向点C运动,同时点Q以5 cm/s的速度从点C向点A运动,它们都依次沿△ABC三边运动,则经过多长时间,点Q第一次在△ABC的哪条边上追上点P?
参考答案
1. A 2. B 3. SAS AB
4.解:因为AB∥CD,所以∠ABO=∠CDO.
又因为OD⊥CD,所以∠CDO=90°
所以∠ABO=90°,即BO⊥AB
因为AB∥OH∥CD(相邻两平行线间的距离相等),所以OB=OD.
在△ABO和△CDO中,因为∠ABO=∠CDO,OB=OD,∠AOB=∠COD,
所以△ABO≌△CDO(ASA)所以AB=CD=20m.
即标语CD的长度为20m.
5.解:两根钢丝的固定符合要求。
理由:由题意可知AO⊥BC,OB=OC,所以∠AOB=∠AOC=90°
在△AOB和△AOC中,因为所以△AOB≌△AOC(SAS),
所以∠BAO=∠CAO.故两根钢丝的固定符合要求。
6.B
7.C 【解析】因为AC=DB,AO=DO,所以OB=OC.又因为∠AOB=∠DOC,所以△AOB≌△DOC.所以AB=CD=100 m。
8. SAS
9.解:在△BDE和△FDM中,因为所以△BDE≌△FDM(SAS).
所以∠BED=∠FMD,即∠BEM=∠FME,所以BE∥MF,
因为AB∥MF,所以A,C,E三点在一条直线上。
10.解:(1)如图所示.
(2)在湖岸上选一点O,连接BO并延长到点C,使BO=OC,连接AO并延长到点D,使OD=AO,连接CD,则AB=CD.测量DC的长度即为AB的长度.
(3)设CD=m.
因为BO=CO,∠AOB=∠COD,AO=DO,所以△AOB≌△DOC(SAS)
所以AB=CD=m.
11.解:(1)①因为BP=3×1=3,CQ=3×1=3,所以BP=CQ.
因为D为AB的中点,所以BD=AD=5.
因为CP=BC-BP=5,所以BD=CP.
在△BPD和△CQP中,因为所以△BPD≌△CQP
②设点Q运动时间为t s,运动速度为v cm/s
因为△BPD≌△CPQ,所以BP=CP=4,CQ=5.
所以,所以。
即当点Q的速度为cm/s时,能使△BPD≌△CPQ。
(2)设经过x秒后,点Q第一次追上点P,
由题意得5x-3x=2×10,解得x=10.
所以点P运动的路程为3×10=30.
因为30=28+2,
所以此时点P在BC边上,
所以经过10 s,点Q第一次在△ABC的BC边上追上点P.
_21?????????è?????(www.21cnjy.com)_
