人教版八年级数学上册数学11.2.1三角形的内角课件(共19张PPT)
文档属性
| 名称 | 人教版八年级数学上册数学11.2.1三角形的内角课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-13 14:26:08 | ||
图片预览




文档简介
(共19张PPT)
与三角形有关的角
三角形的内角
11.2
想一想
三角形的三个内角和是多少?
有什么办法可以验证呢?
三角形的三个内角和等于180°
结论对任意三角形都成立吗?
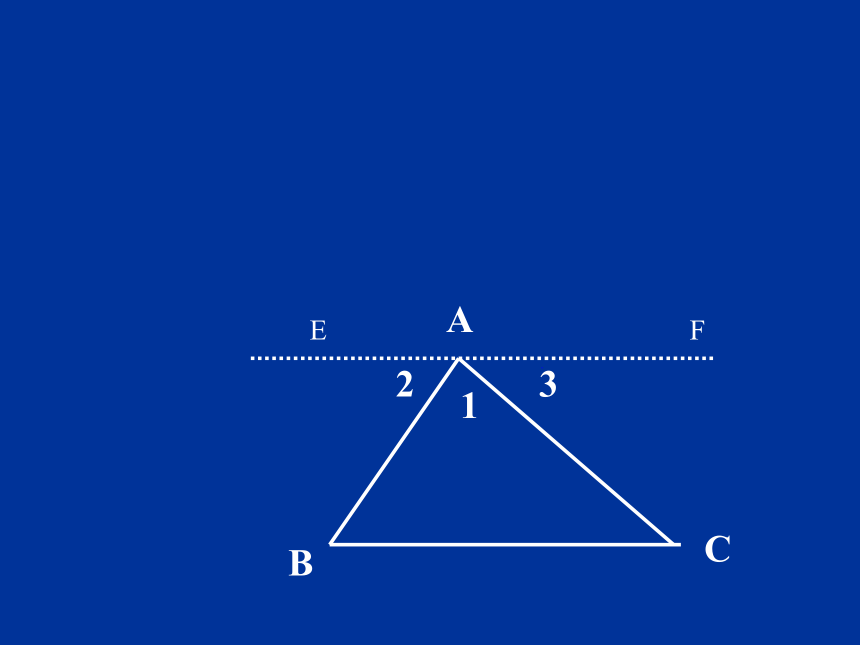
A
B
C
1
2
3
E
F
A
B
C
1
2
3
E
F
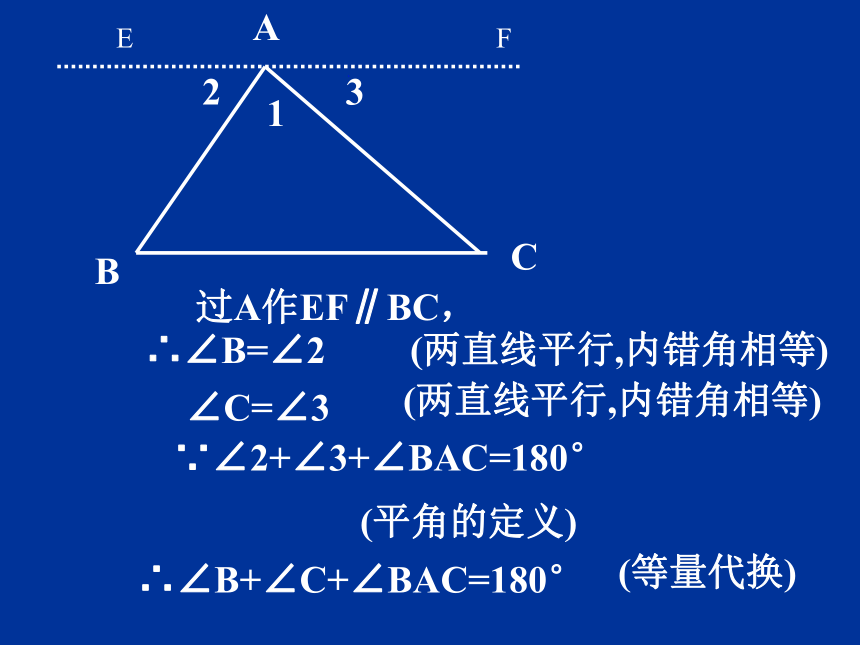
过A作EF∥BC,
∴∠B=∠2
(两直线平行,内错角相等)
∠C=∠3
(两直线平行,内错角相等)
∵∠2+∠3+∠BAC=180°
∴∠B+∠C+∠BAC=180°
(平角的定义)
(等量代换)
A
B
C
A
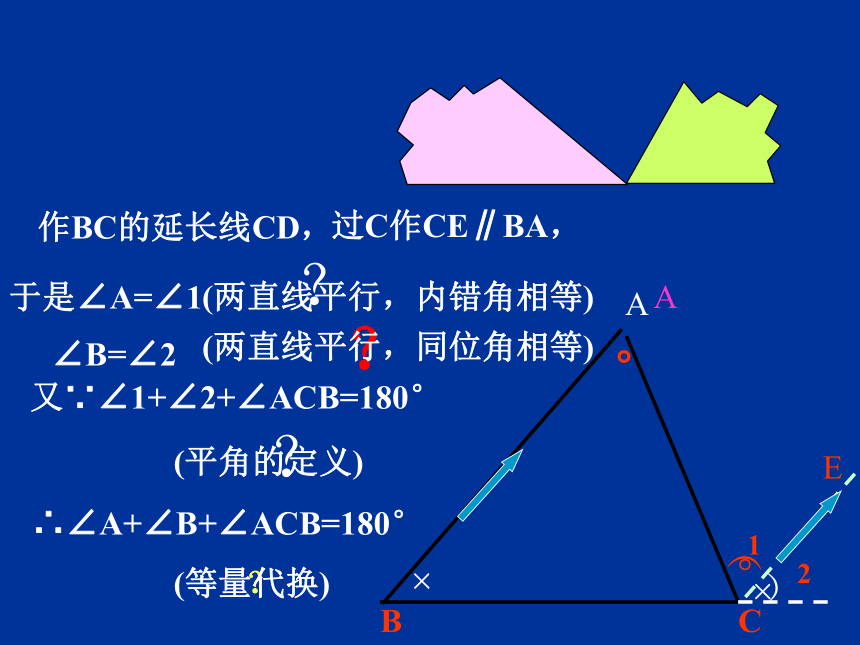
过C作CE∥BA,
)
E
1
)
。
。
于是∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
又∵∠1+∠2+∠ACB=180°
(平角的定义)
∴∠A+∠B+∠ACB=180°
2
×
×
?
?
(两直线平行,同位角相等)
?
?
(等量代换)
作BC的延长线CD,
思路总结
为了说明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
三角形内角和定理:
三角形的内角和等于1800.
(1)在△ABC中,∠A=35°,∠
B=43
°
则∠
C=
.
(2)在△ABC中,
∠A
:∠B:∠C=2:3:4
则∠A
=
∠
B=
∠
C=
.
(1)一个三角形中最多有
个直角?为什么?
(2)一个三角形中最多有
个钝角?为什么?
(3)一个三角形中至少有
个锐角?为什么?
(4)任意
一个三角形中,最大的一个角的度数至少为
.
102
°
80
°
60
°
40
°
60°
2
1
1
复习旧知
讨论
例1:在△ABC中,∠BAC=40度,
∠B=75度,AD是△ABC的角平分线。求∠ADB的度数。
C
D
B
A
例题
2
如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80
°方向,C岛在B岛的北偏西40
°方向。从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
解:
∠CAB=∠BAD-∠CAD=800-500=300
由AD∥BE,可得
∠BAD+∠ABE=1800
所以∠ABE=1800-∠BAD
=1800-800=1000
∠ABC=∠ABE-∠EBC
=1000-400=600
在ΔABC中,
∠ACB=1800-∠ABC-∠CAB
=1800-600-300=900
答:从C岛看A、B两岛的视角∠ACB是900
。
还有其它方法吗?
B
你能想出一个更简捷的方法来求∠C的度数吗?
1
2
50°
40°
解:
过点C画CF∥AD
∴
∠1=∠DAC=50
°,
F
∵
CF∥AD,
又AD
∥BE
∴
CF∥
BE
∴∠2=∠CBE
=40
°
∴
∠ACB=∠1﹢∠2
=50
°﹢
40
°
=90
°
如图,从A处观测C处时仰角∠CAD=30°,从B处观测C处时仰角∠CBD=45°。
从C处观测A、B两处时视角
∠ACB是多少?
练一练
A
B
C
D
解:在△ACD中
∠CAD
=30
°
∠D
=90
°
∴
∠ACD
=180
°
-30
°
-90
°=6
0
°
在△BCD中
∠CBD
=
45
°
∠D
=90
°
∴
∠BCD
=
180
°-90°-45
°=45
°
∴
∠ACB
=
∠ACD
-∠BCD
=
6
0
°-45
°
=15°
2.
如图,一种滑翔伞是左右对称的四边形ABCD,其中∠A=150°,∠B=∠D=40°。求∠C的度数。
D
解:在△ABC中
∠B+∠1+∠BAC=180°
在△ACD中
∠D+∠2+∠DAC=180°
∴∠B+∠D+∠1+∠2+∠BAC+∠CAD=360
°
即
∠B+∠D+
∠BCD
+∠BAD=
360
°
40
°+40
°+
∠BCD
+150
°
=
360
°
∴
∠BCD
=
360
°-40
°-40
°-
150
°
=130
°
1、如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是
(
)
(A)带①去 (B)带②去 (C)带③去 (D)带①和②去
C
练习
例
已知:在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,
求∠DBC的度数.
分析:∠DBC在△BDC中,∠BDC=900,为求∠DBC的度数,只要求出∠C的度数即可.
解:设∠A=
x
,则∠C=∠ABC=2x.
∴x+
2x+
2x=180(三角形内角和定理).
解方程,得x=360.
∴
∠C=2×360=720.
在△BDC中,
∵∠BDC=900(已知),
∴∠DBC=1800-900-720(三角形内角和定理).
∴∠DBC=180.
A
B
C
D
一
、选择题
(1)
在△ABC中,∠A:∠B:∠C
=1:2:3,则∠B
=(
)
A.
300
B.
600
C.
900
D.
1200
(2)
在△ABC中,∠A
=500,
∠B
=800,则∠C
=(
)
A.
400
B.
500
C.
100
D.
1100
(3)在△ABC中,∠A
=800,
∠B
=∠C,则∠B
=(
)
A.
500
B.
400
C.
100
D.
450
二、填空
(1)∠A:∠B:∠C=3:4:5,则∠B
=
(2)∠C
=900,∠A
=300,则∠B
=
(3)∠B
=800,∠A
=3∠C,则∠A
=
B
600
750
B
600
A
3.
在△ABC中,已知∠A-∠C=250,∠B-∠A=100,求∠B的度数.
分析:根据三角形内角和定理可知:
∠A+∠B+∠C=1800,然后结合已知条件便可以求出.
解:在△ABC中,
∠A+∠B+∠C=1800(三角形內角和定理)
联立∠A-∠C=250,∠B-∠A=100可得,
∠A=650,∠B=750,∠C=400
答:∠B的度数是750.
4.如图:已知在△ABC中,EF与AC交于点G,与BC的延长线交于点F,∠B=450
,∠F=300,∠CGF=700,
求∠A的度数.
A
E
G
F
C
B
这节课你有那些收获?
与三角形有关的角
三角形的内角
11.2
想一想
三角形的三个内角和是多少?
有什么办法可以验证呢?
三角形的三个内角和等于180°
结论对任意三角形都成立吗?
A
B
C
1
2
3
E
F
A
B
C
1
2
3
E
F
过A作EF∥BC,
∴∠B=∠2
(两直线平行,内错角相等)
∠C=∠3
(两直线平行,内错角相等)
∵∠2+∠3+∠BAC=180°
∴∠B+∠C+∠BAC=180°
(平角的定义)
(等量代换)
A
B
C
A
过C作CE∥BA,
)
E
1
)
。
。
于是∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
又∵∠1+∠2+∠ACB=180°
(平角的定义)
∴∠A+∠B+∠ACB=180°
2
×
×
?
?
(两直线平行,同位角相等)
?
?
(等量代换)
作BC的延长线CD,
思路总结
为了说明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
三角形内角和定理:
三角形的内角和等于1800.
(1)在△ABC中,∠A=35°,∠
B=43
°
则∠
C=
.
(2)在△ABC中,
∠A
:∠B:∠C=2:3:4
则∠A
=
∠
B=
∠
C=
.
(1)一个三角形中最多有
个直角?为什么?
(2)一个三角形中最多有
个钝角?为什么?
(3)一个三角形中至少有
个锐角?为什么?
(4)任意
一个三角形中,最大的一个角的度数至少为
.
102
°
80
°
60
°
40
°
60°
2
1
1
复习旧知
讨论
例1:在△ABC中,∠BAC=40度,
∠B=75度,AD是△ABC的角平分线。求∠ADB的度数。
C
D
B
A
例题
2
如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80
°方向,C岛在B岛的北偏西40
°方向。从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
解:
∠CAB=∠BAD-∠CAD=800-500=300
由AD∥BE,可得
∠BAD+∠ABE=1800
所以∠ABE=1800-∠BAD
=1800-800=1000
∠ABC=∠ABE-∠EBC
=1000-400=600
在ΔABC中,
∠ACB=1800-∠ABC-∠CAB
=1800-600-300=900
答:从C岛看A、B两岛的视角∠ACB是900
。
还有其它方法吗?
B
你能想出一个更简捷的方法来求∠C的度数吗?
1
2
50°
40°
解:
过点C画CF∥AD
∴
∠1=∠DAC=50
°,
F
∵
CF∥AD,
又AD
∥BE
∴
CF∥
BE
∴∠2=∠CBE
=40
°
∴
∠ACB=∠1﹢∠2
=50
°﹢
40
°
=90
°
如图,从A处观测C处时仰角∠CAD=30°,从B处观测C处时仰角∠CBD=45°。
从C处观测A、B两处时视角
∠ACB是多少?
练一练
A
B
C
D
解:在△ACD中
∠CAD
=30
°
∠D
=90
°
∴
∠ACD
=180
°
-30
°
-90
°=6
0
°
在△BCD中
∠CBD
=
45
°
∠D
=90
°
∴
∠BCD
=
180
°-90°-45
°=45
°
∴
∠ACB
=
∠ACD
-∠BCD
=
6
0
°-45
°
=15°
2.
如图,一种滑翔伞是左右对称的四边形ABCD,其中∠A=150°,∠B=∠D=40°。求∠C的度数。
D
解:在△ABC中
∠B+∠1+∠BAC=180°
在△ACD中
∠D+∠2+∠DAC=180°
∴∠B+∠D+∠1+∠2+∠BAC+∠CAD=360
°
即
∠B+∠D+
∠BCD
+∠BAD=
360
°
40
°+40
°+
∠BCD
+150
°
=
360
°
∴
∠BCD
=
360
°-40
°-40
°-
150
°
=130
°
1、如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是
(
)
(A)带①去 (B)带②去 (C)带③去 (D)带①和②去
C
练习
例
已知:在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,
求∠DBC的度数.
分析:∠DBC在△BDC中,∠BDC=900,为求∠DBC的度数,只要求出∠C的度数即可.
解:设∠A=
x
,则∠C=∠ABC=2x.
∴x+
2x+
2x=180(三角形内角和定理).
解方程,得x=360.
∴
∠C=2×360=720.
在△BDC中,
∵∠BDC=900(已知),
∴∠DBC=1800-900-720(三角形内角和定理).
∴∠DBC=180.
A
B
C
D
一
、选择题
(1)
在△ABC中,∠A:∠B:∠C
=1:2:3,则∠B
=(
)
A.
300
B.
600
C.
900
D.
1200
(2)
在△ABC中,∠A
=500,
∠B
=800,则∠C
=(
)
A.
400
B.
500
C.
100
D.
1100
(3)在△ABC中,∠A
=800,
∠B
=∠C,则∠B
=(
)
A.
500
B.
400
C.
100
D.
450
二、填空
(1)∠A:∠B:∠C=3:4:5,则∠B
=
(2)∠C
=900,∠A
=300,则∠B
=
(3)∠B
=800,∠A
=3∠C,则∠A
=
B
600
750
B
600
A
3.
在△ABC中,已知∠A-∠C=250,∠B-∠A=100,求∠B的度数.
分析:根据三角形内角和定理可知:
∠A+∠B+∠C=1800,然后结合已知条件便可以求出.
解:在△ABC中,
∠A+∠B+∠C=1800(三角形內角和定理)
联立∠A-∠C=250,∠B-∠A=100可得,
∠A=650,∠B=750,∠C=400
答:∠B的度数是750.
4.如图:已知在△ABC中,EF与AC交于点G,与BC的延长线交于点F,∠B=450
,∠F=300,∠CGF=700,
求∠A的度数.
A
E
G
F
C
B
这节课你有那些收获?
