人教版八年级数学上册数学11.1.1 三角形的边课件(共16张PPT)
文档属性
| 名称 | 人教版八年级数学上册数学11.1.1 三角形的边课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 512.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-13 14:13:13 | ||
图片预览





文档简介
(共16张PPT)
第十一章
三角形
11.1.1
三角形的边
学习目标
1.理解、识记三角形的概念及分类;
2.理解并能正确运用“三角形两边的和大于第三边”的性质.
自学指导
认真看课本(第十一章引言--P4练习前)要求:
1.什么是三角形,思考“首尾顺次相接”是什么含义;
2.思考三角形按边的相等关系如何分类;
3.想一想“探究”中的问题,思考为什么“三角形两边的和大于第三边,两边的差小于第三边”
;
4.思考例题(2)中为什么分两种情况讨论,又是如何运用三角形三边关系的.
如有疑问,可小声问同桌或举手问老师.
6分钟后,比谁能准确回答以上问题,并能运用三边关系做对检测题.
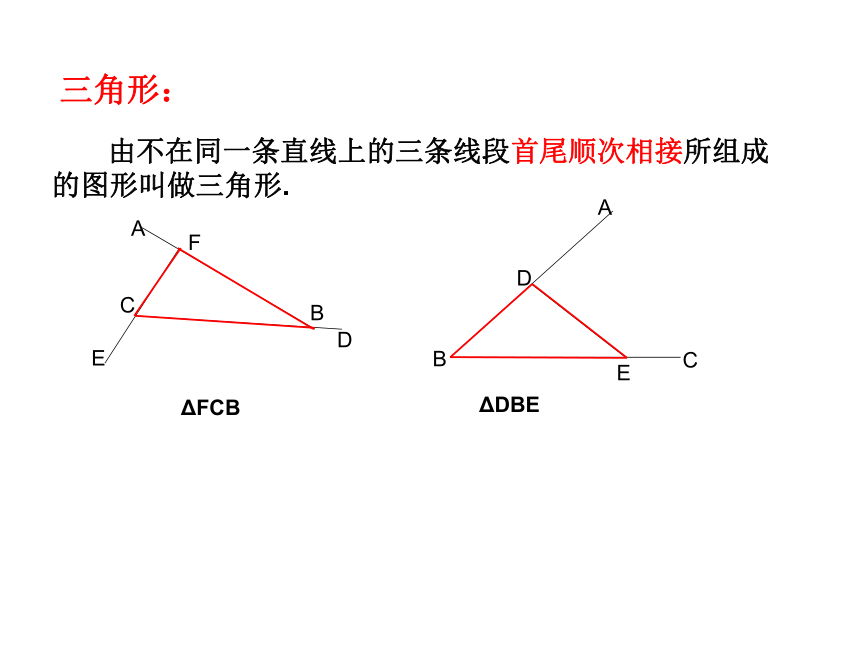
三角形:
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
A
F
C
E
D
B
ΔFCB
D
A
C
B
E
ΔDBE
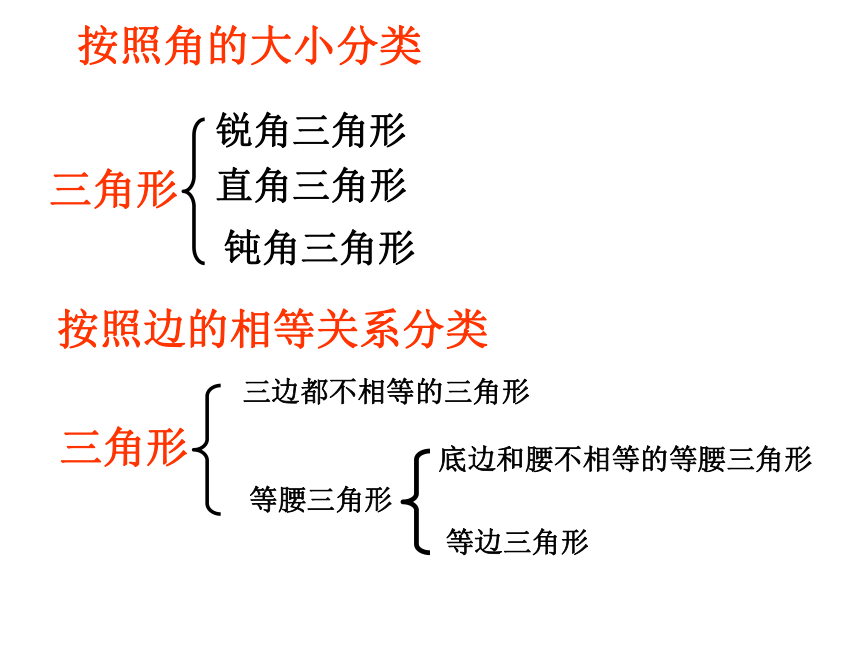
按照角的大小分类
锐角三角形
直角三角形
钝角三角形
三角形
三边都不相等的三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
三角形
按照边的相等关系分类
下列各组数中,不可能成为一个三角形三边长的是(
)
A.2,3,4
B.5,7,7
C.5,6,12
D.6,8,10
C
判断三条线段能否组成三角形的简便方法:
当较小两边的和大于第三边时,能组成三角形
自学检测题
1.图中有几个三角形?用符号表示这些三角形.
2.下列每组数分别是三根木棒的长度,能用它们摆成三角形的是(
)
A
.3,4,8
B.5,6,11
C.5,6,10
D.13,12,30
3.若一个三角形的两条边长分别是3和7,则第三边长可能是(
)
A.6
B.3
C.2
D.11
4.已知等腰三角形的一边长等于4,一边长等于9,求它的周长.
?拓展题:若三角形两边长分别为5和8,则最长边的长x的取值范围
.
要求:1.7分钟独立完成.
2.第4题过程规范,还要求周长.
答案
图中有五个三角形,分别是ΔABE,ΔBCE,ΔCDE,ΔABC,ΔBCD
2.下列每组数分别是三根木棒的长度,能用它们摆成三角形的是(C)
A
.3,4,8
B.5,6,11
C.5,6,10
D.13,12,30
3.若一个三角形的两条边长分别是3和7,则第三边长可能是(A)
A.6
B.3
C.2
D.11
4.已知等腰三角形的一边长等于4,一边长等于9,求它的周长.
解:分两种情况讨论:
①当腰长为4,底边长为9时,4+4<9,不能构成三角形,舍去;
②当腰长为9,底边长为4时,4+9>9,可以构成三角形,此时,
C
=
4+9+9
=
22
∴它的周长为22.
拓展题:若三角形两边长分别为5和8,则最长边的长x的取值范围
8≤X<13
口答题:
1.长为10,7,5,3的四根木条,选其中三根组成三角形,有几种选法?
解:有两种选法,分别是10,7,5;
7,5,3.
当堂训练题
1.已知等腰三角形一边长为5cm,另一边长为10cm,那么第三边长应为
(
)
A.5cm
B.10cm
C.5cm或10cm
D.12cm
2.已知等腰三角形两边长分别为5和6,则这个三角形的周长为(
)
A.11
B.16
C.17
D.16或17
当堂训练题
3.一个等腰三角形的一边长为6cm,周长为20cm,求其他两边的长.
4.已知等腰三角形的一边长为5,一边长为6,求它的周长.
拓展题:
若a,b,c表示ΔABC的三边长,则
=__________.
1.现有两根木棒,它们的长度分别为20cm和30cm,若不改变木棒的长度,要钉成一个三角形木架,应在下列四根木棒中选取
(
)
A.10cm的木棒
B.20cm的木棒
C.50cm的木棒
D.60cm的木棒
2.已知等腰三角形的两边长分别为3和6,则它的周长为(
)
A.9
B.12
C.15
D.12或15
3.已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为(
)
A.2cm
B.3cm
C.4cm
D.5cm
一、选择题:
B
C
B
【跟踪训练】
5.若五条线段的长分别是2cm,3cm,4cm,5cm,则以其中三条线段为边可构成______个三角形。
二、填空题:
6.若等腰三角形的两边长分别为3和7,则它的周长为_______;
若等腰三角形的两边长分别是3和4,则它的周长为
。
7.如果以5cm为等腰三角形的一边,另一边为10cm,则它的周长为________。
3
10或11
17
25cm
8、两根木棒长分别为3厘米和5厘米,要选择第三根木棒钉成三角形,若第三边长是偶数,则第三根长是多少?
9.
已知等腰三角形的一边等于7,一边等于8,
则它的周长是____.
10.等腰三角形的其中一个角是40度,则另两个
角是____.
22或23
40和100度或70和70度
11、如图,点P是⊿ABC内一点,试证明:AB+AC>PB+PC.
作业:
课本P8,第1,2题
第十一章
三角形
11.1.1
三角形的边
学习目标
1.理解、识记三角形的概念及分类;
2.理解并能正确运用“三角形两边的和大于第三边”的性质.
自学指导
认真看课本(第十一章引言--P4练习前)要求:
1.什么是三角形,思考“首尾顺次相接”是什么含义;
2.思考三角形按边的相等关系如何分类;
3.想一想“探究”中的问题,思考为什么“三角形两边的和大于第三边,两边的差小于第三边”
;
4.思考例题(2)中为什么分两种情况讨论,又是如何运用三角形三边关系的.
如有疑问,可小声问同桌或举手问老师.
6分钟后,比谁能准确回答以上问题,并能运用三边关系做对检测题.
三角形:
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
A
F
C
E
D
B
ΔFCB
D
A
C
B
E
ΔDBE
按照角的大小分类
锐角三角形
直角三角形
钝角三角形
三角形
三边都不相等的三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
三角形
按照边的相等关系分类
下列各组数中,不可能成为一个三角形三边长的是(
)
A.2,3,4
B.5,7,7
C.5,6,12
D.6,8,10
C
判断三条线段能否组成三角形的简便方法:
当较小两边的和大于第三边时,能组成三角形
自学检测题
1.图中有几个三角形?用符号表示这些三角形.
2.下列每组数分别是三根木棒的长度,能用它们摆成三角形的是(
)
A
.3,4,8
B.5,6,11
C.5,6,10
D.13,12,30
3.若一个三角形的两条边长分别是3和7,则第三边长可能是(
)
A.6
B.3
C.2
D.11
4.已知等腰三角形的一边长等于4,一边长等于9,求它的周长.
?拓展题:若三角形两边长分别为5和8,则最长边的长x的取值范围
.
要求:1.7分钟独立完成.
2.第4题过程规范,还要求周长.
答案
图中有五个三角形,分别是ΔABE,ΔBCE,ΔCDE,ΔABC,ΔBCD
2.下列每组数分别是三根木棒的长度,能用它们摆成三角形的是(C)
A
.3,4,8
B.5,6,11
C.5,6,10
D.13,12,30
3.若一个三角形的两条边长分别是3和7,则第三边长可能是(A)
A.6
B.3
C.2
D.11
4.已知等腰三角形的一边长等于4,一边长等于9,求它的周长.
解:分两种情况讨论:
①当腰长为4,底边长为9时,4+4<9,不能构成三角形,舍去;
②当腰长为9,底边长为4时,4+9>9,可以构成三角形,此时,
C
=
4+9+9
=
22
∴它的周长为22.
拓展题:若三角形两边长分别为5和8,则最长边的长x的取值范围
8≤X<13
口答题:
1.长为10,7,5,3的四根木条,选其中三根组成三角形,有几种选法?
解:有两种选法,分别是10,7,5;
7,5,3.
当堂训练题
1.已知等腰三角形一边长为5cm,另一边长为10cm,那么第三边长应为
(
)
A.5cm
B.10cm
C.5cm或10cm
D.12cm
2.已知等腰三角形两边长分别为5和6,则这个三角形的周长为(
)
A.11
B.16
C.17
D.16或17
当堂训练题
3.一个等腰三角形的一边长为6cm,周长为20cm,求其他两边的长.
4.已知等腰三角形的一边长为5,一边长为6,求它的周长.
拓展题:
若a,b,c表示ΔABC的三边长,则
=__________.
1.现有两根木棒,它们的长度分别为20cm和30cm,若不改变木棒的长度,要钉成一个三角形木架,应在下列四根木棒中选取
(
)
A.10cm的木棒
B.20cm的木棒
C.50cm的木棒
D.60cm的木棒
2.已知等腰三角形的两边长分别为3和6,则它的周长为(
)
A.9
B.12
C.15
D.12或15
3.已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为(
)
A.2cm
B.3cm
C.4cm
D.5cm
一、选择题:
B
C
B
【跟踪训练】
5.若五条线段的长分别是2cm,3cm,4cm,5cm,则以其中三条线段为边可构成______个三角形。
二、填空题:
6.若等腰三角形的两边长分别为3和7,则它的周长为_______;
若等腰三角形的两边长分别是3和4,则它的周长为
。
7.如果以5cm为等腰三角形的一边,另一边为10cm,则它的周长为________。
3
10或11
17
25cm
8、两根木棒长分别为3厘米和5厘米,要选择第三根木棒钉成三角形,若第三边长是偶数,则第三根长是多少?
9.
已知等腰三角形的一边等于7,一边等于8,
则它的周长是____.
10.等腰三角形的其中一个角是40度,则另两个
角是____.
22或23
40和100度或70和70度
11、如图,点P是⊿ABC内一点,试证明:AB+AC>PB+PC.
作业:
课本P8,第1,2题
