人教版数学八年级上册 11.1 与三角形有关的线段课件(第1课时 共19张PPT)
文档属性
| 名称 | 人教版数学八年级上册 11.1 与三角形有关的线段课件(第1课时 共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 484.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-13 14:17:49 | ||
图片预览






文档简介
(共19张PPT)
11.1.1三角形的边
人教版八年级数学上册
观察图片,都有什么样的形象?在我们生活中有这样的形象吗?能举一些例子吗?
读一读
什么样的图形叫三角形?
什么是三角形的边,顶点,内角。
如何用符号语言表示一个三角形。
课本2页,并回答以下问题:
你认识三角形了吗?
自主预习
三角形的定义
:
由不在同一条直线上的三条线段首尾顺次相接所组成的图形,叫做三角形。
注意点:
(1)三条线段(2)不在同一直线上
(3)首尾顺次相接
A
C
B
1.线段AB、BC、CA
2.点A、B、C
3.∠
A、
∠
B、
∠
C
三角形ABC的三边,有时也用a、b、c来表示.
一般的顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作c
a
b
c
叫做三角形的边
叫做三角形的顶点
叫做三角形的内角,简称三角形的角。
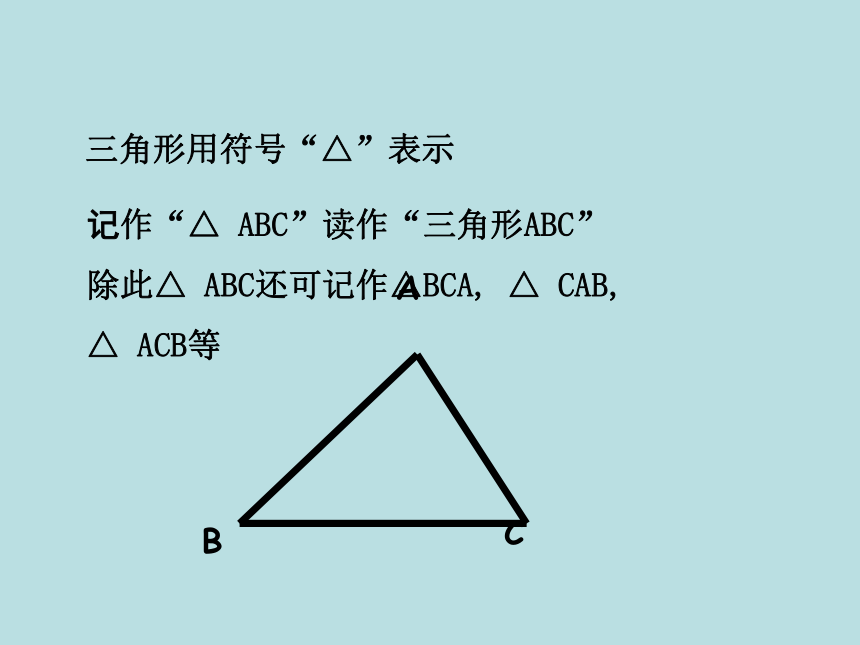
三角形用符号“△”表示
记作“△
ABC”读作“三角形ABC”
除此△
ABC还可记作△BCA,
△
CAB,
△
ACB等
1.图中有几个三角形?用符号表示这些三角形。
2.以AB为边的三角形有哪些?
△ABC、△ABE
3.以E为顶点的三角形有哪些?
△
ABE
、△BCE、
△CDE
试一试
ΔABEΔABC
ΔBECΔBCD
ΔECD
4.说出其中ΔBCD的三个角
∠BCD
、CBD
、∠D
想一想
三角形按照三个角的大小都有哪些三角形呢?
(锐角三角形
直角三角形
钝角三角形)
三角形按照三条边长的大小关系又有哪些三角形呢?
(等边三角形
等腰三角形
不等边三角形)
思考:等腰三角形与等边三角形有什么共同之处?
三角形都可以怎样进行分类?
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
三角形的分类
相等的两条边都叫腰,另一边叫做底,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
腰
腰
底
顶角
底角
底角
如图三角形中,假设有一只小虫要从点B点发
沿着三角形的边爬到点C,它有几条路线可以
选择?各条路线的长一样吗?
路线1:由点B到点C
路线2:由点B到点A,再由点A到点C。
两条路线长分别是BC,AB+AC.
由“两点之间,线段最短”可以得到AB+AC>BC
同理可得:AC+BC>AB,AB+BC>AC
三角形的三边有这样的关系:
三角形两边的和大于第三边
自主探究
三角形两边的差小于第三边.
在一个三角形中,任何两边之差与第三边有什么关系?
(请同学们自己在本子上任意画一个三角形,量出三边的长,再用任何两边的差与第三边比较,得出什么样的结论?)
注意:
1.一个三角形的三边关系可以归纳成如下一句话:三角形的任何两边之和大于第三边,任何两边之差小于第三边.
2.在做题时,不仅要考虑到两边之和大于第三边,还必须考虑到两边之差小于第三边.
练习1.以长为3㎝,5㎝,7㎝,10㎝的四条线段中的三条为边,可以构成三角形的个数是(
)
A、1个
B、
2个
C、
3个
D、4个
B
随堂练习
练习2.下列长度的三条线段能否组成三角形?为什么?
(1)
3,4,8
(
)
(2)
2,5,6
(
)
(3)
4,6,10
(
)
能
不能
不能
练习3.
已知等腰三角形的一边等于7,一边等于8,求它的周长。
已知等腰三角形的一边等于6,一边等于13,求它的周长。
你有什么收获?
这节课你印象最深的是什么?
还有什么不明白的吗?
知识梳理
宇宙之大,粒子之微,火箭之速,化工之
巧,地球之变,生物之谜,日用之繁,无处
不用数学。
——华罗庚
结束语
11.1.1三角形的边
人教版八年级数学上册
观察图片,都有什么样的形象?在我们生活中有这样的形象吗?能举一些例子吗?
读一读
什么样的图形叫三角形?
什么是三角形的边,顶点,内角。
如何用符号语言表示一个三角形。
课本2页,并回答以下问题:
你认识三角形了吗?
自主预习
三角形的定义
:
由不在同一条直线上的三条线段首尾顺次相接所组成的图形,叫做三角形。
注意点:
(1)三条线段(2)不在同一直线上
(3)首尾顺次相接
A
C
B
1.线段AB、BC、CA
2.点A、B、C
3.∠
A、
∠
B、
∠
C
三角形ABC的三边,有时也用a、b、c来表示.
一般的顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作c
a
b
c
叫做三角形的边
叫做三角形的顶点
叫做三角形的内角,简称三角形的角。
三角形用符号“△”表示
记作“△
ABC”读作“三角形ABC”
除此△
ABC还可记作△BCA,
△
CAB,
△
ACB等
1.图中有几个三角形?用符号表示这些三角形。
2.以AB为边的三角形有哪些?
△ABC、△ABE
3.以E为顶点的三角形有哪些?
△
ABE
、△BCE、
△CDE
试一试
ΔABEΔABC
ΔBECΔBCD
ΔECD
4.说出其中ΔBCD的三个角
∠BCD
、CBD
、∠D
想一想
三角形按照三个角的大小都有哪些三角形呢?
(锐角三角形
直角三角形
钝角三角形)
三角形按照三条边长的大小关系又有哪些三角形呢?
(等边三角形
等腰三角形
不等边三角形)
思考:等腰三角形与等边三角形有什么共同之处?
三角形都可以怎样进行分类?
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
三角形的分类
相等的两条边都叫腰,另一边叫做底,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
腰
腰
底
顶角
底角
底角
如图三角形中,假设有一只小虫要从点B点发
沿着三角形的边爬到点C,它有几条路线可以
选择?各条路线的长一样吗?
路线1:由点B到点C
路线2:由点B到点A,再由点A到点C。
两条路线长分别是BC,AB+AC.
由“两点之间,线段最短”可以得到AB+AC>BC
同理可得:AC+BC>AB,AB+BC>AC
三角形的三边有这样的关系:
三角形两边的和大于第三边
自主探究
三角形两边的差小于第三边.
在一个三角形中,任何两边之差与第三边有什么关系?
(请同学们自己在本子上任意画一个三角形,量出三边的长,再用任何两边的差与第三边比较,得出什么样的结论?)
注意:
1.一个三角形的三边关系可以归纳成如下一句话:三角形的任何两边之和大于第三边,任何两边之差小于第三边.
2.在做题时,不仅要考虑到两边之和大于第三边,还必须考虑到两边之差小于第三边.
练习1.以长为3㎝,5㎝,7㎝,10㎝的四条线段中的三条为边,可以构成三角形的个数是(
)
A、1个
B、
2个
C、
3个
D、4个
B
随堂练习
练习2.下列长度的三条线段能否组成三角形?为什么?
(1)
3,4,8
(
)
(2)
2,5,6
(
)
(3)
4,6,10
(
)
能
不能
不能
练习3.
已知等腰三角形的一边等于7,一边等于8,求它的周长。
已知等腰三角形的一边等于6,一边等于13,求它的周长。
你有什么收获?
这节课你印象最深的是什么?
还有什么不明白的吗?
知识梳理
宇宙之大,粒子之微,火箭之速,化工之
巧,地球之变,生物之谜,日用之繁,无处
不用数学。
——华罗庚
结束语
