1.3 勾股定理的应用(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 1.3 勾股定理的应用(知识清单+经典例题+夯实基础+提优特训+中考链接) |

|
|
| 格式 | zip | ||
| 文件大小 | 510.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-13 00:00:00 | ||
图片预览


文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
北师大版八年级数学上册第一章勾股定理
1.3
勾股定理的应用
【知识清单】
1、能应用勾股定理和勾股定理的逆定理解决一些简单的实际问题;
2、学会构建适当的数学模型应用数形结合的思想,从实际问题中寻找可应用的直角三角形,然后运用直角三角形的性质解决问题.
(1)解决线路最短问题的依据:两点之间线段最短;
(2)几何体上两点之间最短路线的求解策略是:将立体的展开成平面图形.
3、应用勾股定理应该注意的事项:
(1)运用勾股定理的前提是三角形一定是直角三角形初学者往往忽视只有直角三角形才能使用勾股定理这一前提条件而用勾股定理.
(2)运用勾股定理或逆定理解决问题时在没明确直角边及斜边的前提下,不慎重就会造成结果的遗漏.
(3)在一个题目中既要用到勾股定理又要运用勾股定理的逆定理时,要理清所给条件确定两个定理的使用的先后顺序.
【经典例题】
例题1、如图1是我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:
如图所示,把枯木看作一个圆柱体,因一丈是十尺,
则该圆柱的高为20尺,底面周长为3尺,有葛藤自
点A处缠绕而上,绕五周后其末端恰好到达点B处,
则问题中葛藤的最短长度是多少
尺.
【考点】平面展开,最短路径问题,勾股定理的应用.
【分析】这种立体图形求最短路径问题,可以展开成为平面内的问题解决,展开后可转化下图,所以是个直角三角形求斜边的问题,根据勾股定理可求出.
【解答】如图2,一条直角边(即枯木的高)长20尺,
另一条直角边长5×3=15(尺),
所以葛藤长的平方=202+152=625=252
所以葛藤长=25(尺).故答案为:25.
【点评】本题考查了平面展开最短路径问题,关键是把立体图形展成平面图形,本题是展成平面图形后为直角三角形按照勾股定理可求出解.
例题2、如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,已知AC=200米,BD=600米,且CD=600米.
(1)牧童从A处放牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短?
(2)最短路程是多少?
【考点】勾股定理的应用.
【分析】(1)要求牧童行驶距离最短的饮水点P,
只有AP、BP的和为两定点之间的距离,也即是P在
两定点、B的连线上.
(2)作点A关于l的对称点,过作⊥BD交
BD的延长线于点E,求得=CD=600m,BE=BD+DE
=600+200=800(m),然后在Rt中根据勾股定理
求出的长即可.
【解答】(1)作点A关于l的对称点,连接交CD于点P,则点P为所求的点,此时PA+PB=+PB=,就是最短路程.
(2)过作⊥BD的延长线于点E,如图所示,
由题意得=600m,=DE,
所以BE=BD+DE=
BD+=
600+200=800m,
在Rt中,由勾股定理得2=2+BE2
=6002+8002=10002,
所以B=1000
m.
所以最短路程为1000
m.
【点评】本题考查了最短路径的数学问题.这类问题的解答依据是“两点之间,线段最短”,可以利用对称的性质,通过线段等量代换,将所求路线长转化为两定点之间的距离.
【夯实基础】
1、如图,点A和点B分别是棱长为40cm的正方体盒子上相邻面的两个中心,一只蚂蚁在盒子表面由A处向B处爬行,所走最短路程是
(
)
A.40
cm?
B.50?cm?
C.60
cm?
D.70?cm
2、下列满足条件的三角形中,不是直角三角形的是( )
A.三内角之比为1︰3︰4
B.三边长的平方之比为1︰2︰3
C.三边长之比为7︰24:25
D.三内角之比为2︰3︰7
3、如图是某宾馆的一段楼梯,楼梯高9m,楼梯的最高点A与最低点B的距离是15m,且楼梯宽度为2m.若要给此段楼梯铺地毯,已知地毯单价为50元/m2,则铺完该楼梯表面至少需要
(
)元钱?
A.1500
B.2100??
C.2400?
??D.2600
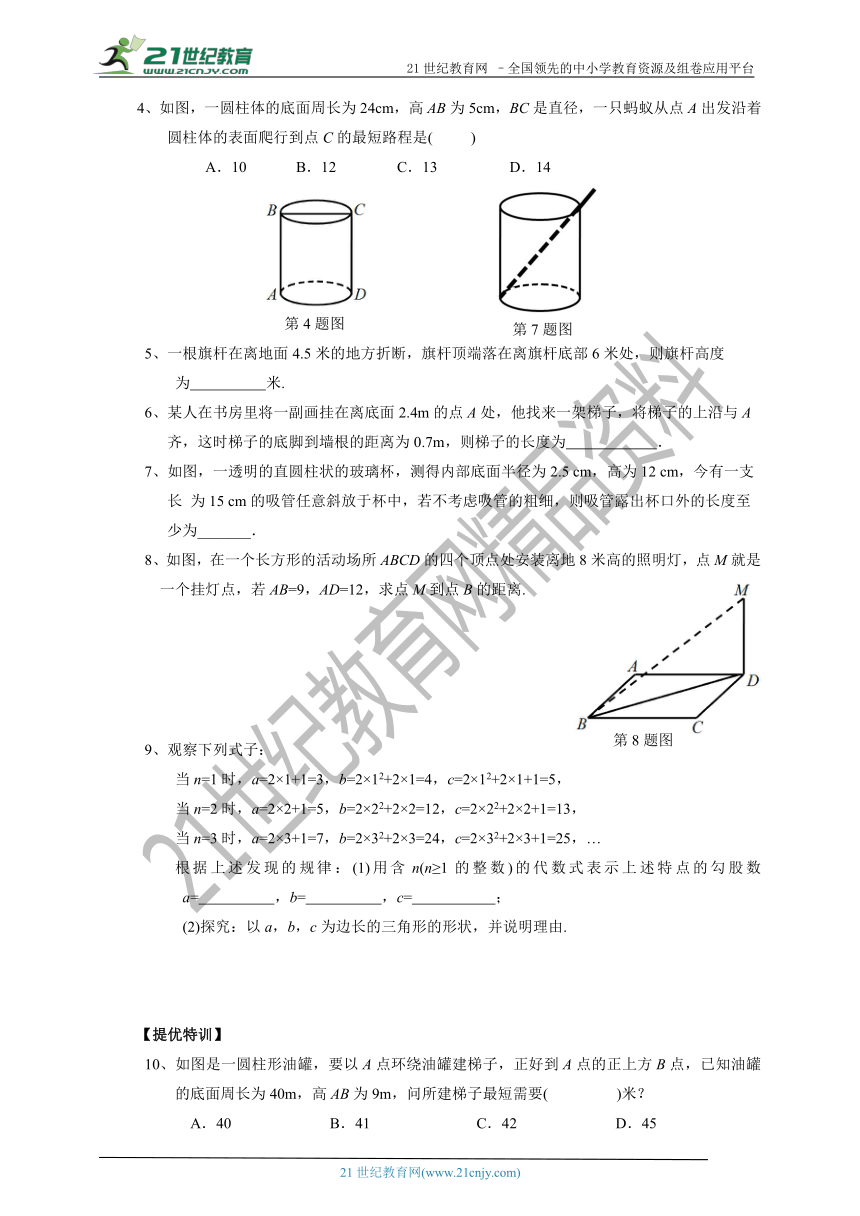
4、如图,一圆柱体的底面周长为24cm,高AB为5cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是(
)
A.10?
B.12??
C.13?
??D.14
5、一根旗杆在离地面4.5米的地方折断,旗杆顶端落在离旗杆底部6米处,则旗杆高度
为
米.
6、某人在书房里将一副画挂在离底面2.4m的点A处,他找来一架梯子,将梯子的上沿与A
齐,这时梯子的底脚到墙根的距离为0.7m,则梯子的长度为
.
7、如图,一透明的直圆柱状的玻璃杯,测得内部底面半径为2.5
cm,高为12
cm,今有一支
长
为15
cm的吸管任意斜放于杯中,若不考虑吸管的粗细,则吸管露出杯口外的长度至
少为_______.
8、如图,在一个长方形的活动场所ABCD的四个顶点处安装离地8米高的照明灯,点M就是一个挂灯点,若AB=9,AD=12,求点M到点B的距离.
9、观察下列式子:
当n=1时,a=2×1+1=3,b=2×12+2×1=4,c=2×12+2×1+1=5,
当n=2时,a=2×2+1=5,b=2×22+2×2=12,c=2×22+2×2+1=13,
当n=3时,a=2×3+1=7,b=2×32+2×3=24,c=2×32+2×3+1=25,…
根据上述发现的规律:(1)用含n(n≥1的整数)的代数式表示上述特点的勾股数
a=
,b=
,c=
;
(2)探究:以a,b,c为边长的三角形的形状,并说明理由.
?
【提优特训】
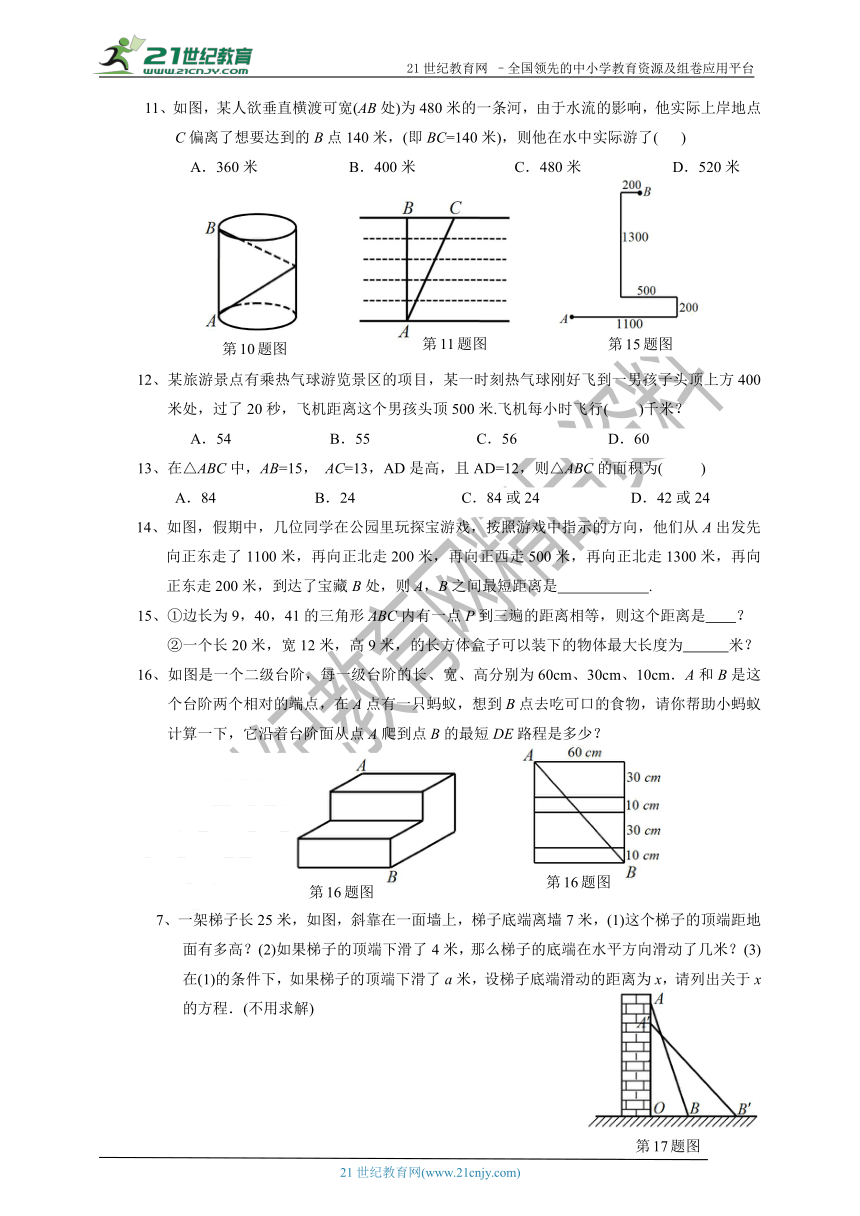
10、如图是一圆柱形油罐,要以A点环绕油罐建梯子,正好到A点的正上方B点,已知油罐的底面周长为40m,高AB为9m,问所建梯子最短需要(
)米?
A.40
B.41
C.42
D.45
11、如图,某人欲垂直横渡可宽(AB处)为480米的一条河,由于水流的影响,他实际上岸地点C偏离了想要达到的B点140米,(即BC=140米),则他在水中实际游了(
)
A.360米
B.400米
C.480米
D.520米
12、某旅游景点有乘热气球游览景区的项目,某一时刻热气球刚好飞到一男孩子头顶上方400米处,过了20秒,飞机距离这个男孩头顶500米.飞机每小时飞行( )千米?
A.54
B.55
C.56
D.60
13、在△ABC中,AB=15,
AC=13,AD是高,且AD=12,则△ABC的面积为(
)
A.84
B.24
C.84或24
D.42或24
14、如图,假期中,几位同学在公园里玩探宝游戏,按照游戏中指示的方向,他们从A出发先向正东走了1100米,再向正北走200米,再向正西走500米,再向正北走1300米,再向正东走200米,到达了宝藏B处,则A,B之间最短距离是
.
15、①边长为9,40,41的三角形ABC内有一点P到三遍的距离相等,则这个距离是
?
②一个长20米,宽12米,高9米,的长方体盒子可以装下的物体最大长度为
米?
16、如图是一个二级台阶,每一级台阶的长、宽、高分别为60cm、30cm、10cm.A和B是这个台阶两个相对的端点,在A点有一只蚂蚁,想到B点去吃可口的食物,请你帮助小蚂蚁计算一下,它沿着台阶面从点A爬到点B的最短DE路程是多少?
?7、一架梯子长25米,如图,斜靠在一面墙上,梯子底端离墙7米,(1)这个梯子的顶端距地面有多高?(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?(3)在(1)的条件下,如果梯子的顶端下滑了a米,设梯子底端滑动的距离为x,请列出关于x的方程.(不用求解)
18、如图所示,A、B两村在一条公路l的同侧,A、B两村到公路的距离分别为AC=3km,BD=5km,又CD=6km,为将A、B两村绿色农产品及时运出去,现要在公路l上建一货运中转站P,使P点到A、B两村的距离的和最短,请你在l上选择货运中转站P的位置,并求出最短距离.
【中考链接】
19、(2018?湘潭)《九章算术》是我国古代最重要的数学著作之一,在“匀股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,则可列方程为
.
20、(2019?宜宾)
如图,已知直角三角形ABC中,CD是斜边AB上的高,AC=4,BC=3,则AD=
.
21、(2019年四川巴中)如图,等腰直角三角板如图放置,直角顶点C在直线m上,分别过点A、B作AE⊥直线m于点E,BD⊥直线m于点D.
①求证:EC=BD.
②若设△AEC三边分别为a、b、c,
利用此图证明勾股定理.
参考答案
1、A
2、D
3、B
4、C
5、12
6、2.5m
7、2
10、B
11、D
12、A
13、C
14、1500米
15、4,
25
19、x2+32=(10﹣x)2
20、
8、如图,在一个长方形的活动场所ABCD的四个顶点处安装离地8米高的照明灯,点M就是一个挂灯点,若AB=9,AD=12,求点M到点B的距离.
解:在Rt△ABD中,
BD2=AB2+AD2=92+122=225=152,
∴BD=15,
在Rt△BMD中,DM=8,
BM2=BD2+DM2=152+82=289=172,
∴BM=17,
答:点M到点B的距离17m.
9、观察下列式子:
当n=1时,a=2×1+1=3,b=2×12+2×1=4,c=2×12+2×1+1=5,
当n=2时,a=2×2+1=5,b=2×22+2×2=12,c=2×22+2×2+1=13,
当n=3时,a=2×3+1=7,b=2×32+2×3=24,c=2×32+2×3+1=25,…
根据上述发现的规律:(1)用含n(n≥1的整数)的代数式表示上述特点的勾股数
a=
,b=
,c=
;
(2)探究:以a,b,c为边长的三角形的形状,并说明理由.
?
解:(1)a=2n+1,b=2n2+2n,c=2n2+2n
+1.
答案为:2n+1,
2n2+2n,
2n2+2n
+1;
(2)以a,b,c为边长的三角形是直角三角形,理由如下:
∵a2+b2=(2n+1)2+(2n2+2n)2=4n2+4n+1+4n4+8n3+4n2=4n4+8n3+8n2+4n+
1,
c2=(2n2+2n
+1)2=(2n2+2n)2+2(2n2+2n)
+1=4n4+8n3+4n2+4n2+4n+1=4n4+8n3+8n2+4n+
1,
∴a2+b2=
c2.
∴以a,b,c为边长的三角形是直角三角形.
16、如图是一个二级台阶,每一级台阶的长、宽、高分别为60cm、30cm、10cm.A和B是这个台阶两个相对的端点,在A点有一只蚂蚁,想到B点去吃可口的食物,请你帮助小蚂蚁计算一下,它沿着台阶面从点A爬到点B的最短DE路程是多少?
?解:如图所示,将二级台阶立体图形展成平面图形:
则有AB2=602+(30+30+10+10)2=1002,
所以AB=100cm,
答:它沿着台阶面从点A爬到点B的最短路程是100cm.
17、一架梯子长25米,如图,斜靠在一面墙上,梯子底端离墙7米,(1)这个梯子的顶端距地面有多高?(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?(3)在(1)的条件下,如果梯子的顶端下滑了a米,设梯子底端滑动的距离为x,请列出关于x的方程.(不用求解)
解:(1)由题意得:
BO=7米,
AB=25米,
在RtABO中,根据勾股定理可得:
AO2=
AB2﹣BO2
=625﹣49=
576=242,
AO=24米;
所以这个梯子的顶端距地面有24米高.
(2)由题意得:AA′=4米,则A′O=24﹣4=20米,
在Rt△A′OB′中:(OB′)2=
A′B′
2﹣A′O2
=
625﹣400
=225=152,
OB′=15(米),
BB′=B′O﹣BO=15﹣7=8(米);
答:梯子底部在水平方向不是滑动了4米,而是8米.
(3)AA′=a米,则A′O=24﹣a(米),OB′=7+x,
在Rt△A′OB′中:
OB′2=A′B
′
2﹣A′O
2,
即:(7+x)2=
252﹣(24﹣a
)
2
18、如图所示,A、B两村在一条公路l的同侧,A、B两村到公路的距离分别为AC=3km,BD=5km,又CD=6km,为将A、B两村绿色农产品及时运出去,现要在公路l上建一货运中转站P,使P点到A、B两村的距离的和最短,请你在l上选择货运中转站P的位置,并求出最短距离.
解答:作出点A关于l的对称点,连接交l于点P,
连接AP,根据对称性可知,在点P处建货运中转站能使P
点到A、B两村的距离的和最短.
过点作∥l,交BD的延长线于点E,
∴=CD,=DE,
∵=
AC
=3km,BD=5km,CD=6km,
∴=CD=6km,BE=BD+DE=BD+=5+3=8(km),
在Rt△中,(km),
P点到A、B两村的距离最短为10
km.
21、(2019年四川巴中)如图,等腰直角三角板如图放置,直角顶点C在直线m上,分别过点A、B作AE⊥直线m于点E,BD⊥直线m于点D.
①求证:EC=BD.
②若设△AEC三边分别为a、b、c,
利用此图证明勾股定理.
解:①∵∠ACB=90°,∴∠ACE+∠BCD=90°.
∵BD⊥m,AE⊥m,∴∠CDB=90°,∠AEC=90°,
∴∠ACE+∠CAE=90°.∴∠CAE=∠BCD.
在△AEC和△CDB中,
∵∠AEC=∠CDB=90°,∠CAE=∠BCD,AC=CB,
∴△AEC≌△CDB(AAS),∴EC=BD.
②由①知BD=CE=a,CD=AE=b,∴S梯形ABDE=(a+b)(a+b)=a2+ab+b2.
又∵S梯形ABDE=S△AEC+
S△BCD+S△ABC=ab+ab+c2=ab+c2,
∴a2+ab+b2=ab+c2,∴a2+b2=c2.
即直角三角形两条直角边的平方和等于斜边的平方.
第11题图
第19题图
第20题图
第10题图
第8题图
第4题图
第22题图
第18题图
第1题图
第17题图
第22题图
第15题图
第3题图
第16题图
第8题图
例题2图
第7题图
例题2图
第16题图
例题1图2
第17题图
第16题图
第16题图
例题1图1
第18题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
北师大版八年级数学上册第一章勾股定理
1.3
勾股定理的应用
【知识清单】
1、能应用勾股定理和勾股定理的逆定理解决一些简单的实际问题;
2、学会构建适当的数学模型应用数形结合的思想,从实际问题中寻找可应用的直角三角形,然后运用直角三角形的性质解决问题.
(1)解决线路最短问题的依据:两点之间线段最短;
(2)几何体上两点之间最短路线的求解策略是:将立体的展开成平面图形.
3、应用勾股定理应该注意的事项:
(1)运用勾股定理的前提是三角形一定是直角三角形初学者往往忽视只有直角三角形才能使用勾股定理这一前提条件而用勾股定理.
(2)运用勾股定理或逆定理解决问题时在没明确直角边及斜边的前提下,不慎重就会造成结果的遗漏.
(3)在一个题目中既要用到勾股定理又要运用勾股定理的逆定理时,要理清所给条件确定两个定理的使用的先后顺序.
【经典例题】
例题1、如图1是我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:
如图所示,把枯木看作一个圆柱体,因一丈是十尺,
则该圆柱的高为20尺,底面周长为3尺,有葛藤自
点A处缠绕而上,绕五周后其末端恰好到达点B处,
则问题中葛藤的最短长度是多少
尺.
【考点】平面展开,最短路径问题,勾股定理的应用.
【分析】这种立体图形求最短路径问题,可以展开成为平面内的问题解决,展开后可转化下图,所以是个直角三角形求斜边的问题,根据勾股定理可求出.
【解答】如图2,一条直角边(即枯木的高)长20尺,
另一条直角边长5×3=15(尺),
所以葛藤长的平方=202+152=625=252
所以葛藤长=25(尺).故答案为:25.
【点评】本题考查了平面展开最短路径问题,关键是把立体图形展成平面图形,本题是展成平面图形后为直角三角形按照勾股定理可求出解.
例题2、如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,已知AC=200米,BD=600米,且CD=600米.
(1)牧童从A处放牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短?
(2)最短路程是多少?
【考点】勾股定理的应用.
【分析】(1)要求牧童行驶距离最短的饮水点P,
只有AP、BP的和为两定点之间的距离,也即是P在
两定点、B的连线上.
(2)作点A关于l的对称点,过作⊥BD交
BD的延长线于点E,求得=CD=600m,BE=BD+DE
=600+200=800(m),然后在Rt中根据勾股定理
求出的长即可.
【解答】(1)作点A关于l的对称点,连接交CD于点P,则点P为所求的点,此时PA+PB=+PB=,就是最短路程.
(2)过作⊥BD的延长线于点E,如图所示,
由题意得=600m,=DE,
所以BE=BD+DE=
BD+=
600+200=800m,
在Rt中,由勾股定理得2=2+BE2
=6002+8002=10002,
所以B=1000
m.
所以最短路程为1000
m.
【点评】本题考查了最短路径的数学问题.这类问题的解答依据是“两点之间,线段最短”,可以利用对称的性质,通过线段等量代换,将所求路线长转化为两定点之间的距离.
【夯实基础】
1、如图,点A和点B分别是棱长为40cm的正方体盒子上相邻面的两个中心,一只蚂蚁在盒子表面由A处向B处爬行,所走最短路程是
(
)
A.40
cm?
B.50?cm?
C.60
cm?
D.70?cm
2、下列满足条件的三角形中,不是直角三角形的是( )
A.三内角之比为1︰3︰4
B.三边长的平方之比为1︰2︰3
C.三边长之比为7︰24:25
D.三内角之比为2︰3︰7
3、如图是某宾馆的一段楼梯,楼梯高9m,楼梯的最高点A与最低点B的距离是15m,且楼梯宽度为2m.若要给此段楼梯铺地毯,已知地毯单价为50元/m2,则铺完该楼梯表面至少需要
(
)元钱?
A.1500
B.2100??
C.2400?
??D.2600
4、如图,一圆柱体的底面周长为24cm,高AB为5cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是(
)
A.10?
B.12??
C.13?
??D.14
5、一根旗杆在离地面4.5米的地方折断,旗杆顶端落在离旗杆底部6米处,则旗杆高度
为
米.
6、某人在书房里将一副画挂在离底面2.4m的点A处,他找来一架梯子,将梯子的上沿与A
齐,这时梯子的底脚到墙根的距离为0.7m,则梯子的长度为
.
7、如图,一透明的直圆柱状的玻璃杯,测得内部底面半径为2.5
cm,高为12
cm,今有一支
长
为15
cm的吸管任意斜放于杯中,若不考虑吸管的粗细,则吸管露出杯口外的长度至
少为_______.
8、如图,在一个长方形的活动场所ABCD的四个顶点处安装离地8米高的照明灯,点M就是一个挂灯点,若AB=9,AD=12,求点M到点B的距离.
9、观察下列式子:
当n=1时,a=2×1+1=3,b=2×12+2×1=4,c=2×12+2×1+1=5,
当n=2时,a=2×2+1=5,b=2×22+2×2=12,c=2×22+2×2+1=13,
当n=3时,a=2×3+1=7,b=2×32+2×3=24,c=2×32+2×3+1=25,…
根据上述发现的规律:(1)用含n(n≥1的整数)的代数式表示上述特点的勾股数
a=
,b=
,c=
;
(2)探究:以a,b,c为边长的三角形的形状,并说明理由.
?
【提优特训】
10、如图是一圆柱形油罐,要以A点环绕油罐建梯子,正好到A点的正上方B点,已知油罐的底面周长为40m,高AB为9m,问所建梯子最短需要(
)米?
A.40
B.41
C.42
D.45
11、如图,某人欲垂直横渡可宽(AB处)为480米的一条河,由于水流的影响,他实际上岸地点C偏离了想要达到的B点140米,(即BC=140米),则他在水中实际游了(
)
A.360米
B.400米
C.480米
D.520米
12、某旅游景点有乘热气球游览景区的项目,某一时刻热气球刚好飞到一男孩子头顶上方400米处,过了20秒,飞机距离这个男孩头顶500米.飞机每小时飞行( )千米?
A.54
B.55
C.56
D.60
13、在△ABC中,AB=15,
AC=13,AD是高,且AD=12,则△ABC的面积为(
)
A.84
B.24
C.84或24
D.42或24
14、如图,假期中,几位同学在公园里玩探宝游戏,按照游戏中指示的方向,他们从A出发先向正东走了1100米,再向正北走200米,再向正西走500米,再向正北走1300米,再向正东走200米,到达了宝藏B处,则A,B之间最短距离是
.
15、①边长为9,40,41的三角形ABC内有一点P到三遍的距离相等,则这个距离是
?
②一个长20米,宽12米,高9米,的长方体盒子可以装下的物体最大长度为
米?
16、如图是一个二级台阶,每一级台阶的长、宽、高分别为60cm、30cm、10cm.A和B是这个台阶两个相对的端点,在A点有一只蚂蚁,想到B点去吃可口的食物,请你帮助小蚂蚁计算一下,它沿着台阶面从点A爬到点B的最短DE路程是多少?
?7、一架梯子长25米,如图,斜靠在一面墙上,梯子底端离墙7米,(1)这个梯子的顶端距地面有多高?(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?(3)在(1)的条件下,如果梯子的顶端下滑了a米,设梯子底端滑动的距离为x,请列出关于x的方程.(不用求解)
18、如图所示,A、B两村在一条公路l的同侧,A、B两村到公路的距离分别为AC=3km,BD=5km,又CD=6km,为将A、B两村绿色农产品及时运出去,现要在公路l上建一货运中转站P,使P点到A、B两村的距离的和最短,请你在l上选择货运中转站P的位置,并求出最短距离.
【中考链接】
19、(2018?湘潭)《九章算术》是我国古代最重要的数学著作之一,在“匀股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,则可列方程为
.
20、(2019?宜宾)
如图,已知直角三角形ABC中,CD是斜边AB上的高,AC=4,BC=3,则AD=
.
21、(2019年四川巴中)如图,等腰直角三角板如图放置,直角顶点C在直线m上,分别过点A、B作AE⊥直线m于点E,BD⊥直线m于点D.
①求证:EC=BD.
②若设△AEC三边分别为a、b、c,
利用此图证明勾股定理.
参考答案
1、A
2、D
3、B
4、C
5、12
6、2.5m
7、2
10、B
11、D
12、A
13、C
14、1500米
15、4,
25
19、x2+32=(10﹣x)2
20、
8、如图,在一个长方形的活动场所ABCD的四个顶点处安装离地8米高的照明灯,点M就是一个挂灯点,若AB=9,AD=12,求点M到点B的距离.
解:在Rt△ABD中,
BD2=AB2+AD2=92+122=225=152,
∴BD=15,
在Rt△BMD中,DM=8,
BM2=BD2+DM2=152+82=289=172,
∴BM=17,
答:点M到点B的距离17m.
9、观察下列式子:
当n=1时,a=2×1+1=3,b=2×12+2×1=4,c=2×12+2×1+1=5,
当n=2时,a=2×2+1=5,b=2×22+2×2=12,c=2×22+2×2+1=13,
当n=3时,a=2×3+1=7,b=2×32+2×3=24,c=2×32+2×3+1=25,…
根据上述发现的规律:(1)用含n(n≥1的整数)的代数式表示上述特点的勾股数
a=
,b=
,c=
;
(2)探究:以a,b,c为边长的三角形的形状,并说明理由.
?
解:(1)a=2n+1,b=2n2+2n,c=2n2+2n
+1.
答案为:2n+1,
2n2+2n,
2n2+2n
+1;
(2)以a,b,c为边长的三角形是直角三角形,理由如下:
∵a2+b2=(2n+1)2+(2n2+2n)2=4n2+4n+1+4n4+8n3+4n2=4n4+8n3+8n2+4n+
1,
c2=(2n2+2n
+1)2=(2n2+2n)2+2(2n2+2n)
+1=4n4+8n3+4n2+4n2+4n+1=4n4+8n3+8n2+4n+
1,
∴a2+b2=
c2.
∴以a,b,c为边长的三角形是直角三角形.
16、如图是一个二级台阶,每一级台阶的长、宽、高分别为60cm、30cm、10cm.A和B是这个台阶两个相对的端点,在A点有一只蚂蚁,想到B点去吃可口的食物,请你帮助小蚂蚁计算一下,它沿着台阶面从点A爬到点B的最短DE路程是多少?
?解:如图所示,将二级台阶立体图形展成平面图形:
则有AB2=602+(30+30+10+10)2=1002,
所以AB=100cm,
答:它沿着台阶面从点A爬到点B的最短路程是100cm.
17、一架梯子长25米,如图,斜靠在一面墙上,梯子底端离墙7米,(1)这个梯子的顶端距地面有多高?(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?(3)在(1)的条件下,如果梯子的顶端下滑了a米,设梯子底端滑动的距离为x,请列出关于x的方程.(不用求解)
解:(1)由题意得:
BO=7米,
AB=25米,
在RtABO中,根据勾股定理可得:
AO2=
AB2﹣BO2
=625﹣49=
576=242,
AO=24米;
所以这个梯子的顶端距地面有24米高.
(2)由题意得:AA′=4米,则A′O=24﹣4=20米,
在Rt△A′OB′中:(OB′)2=
A′B′
2﹣A′O2
=
625﹣400
=225=152,
OB′=15(米),
BB′=B′O﹣BO=15﹣7=8(米);
答:梯子底部在水平方向不是滑动了4米,而是8米.
(3)AA′=a米,则A′O=24﹣a(米),OB′=7+x,
在Rt△A′OB′中:
OB′2=A′B
′
2﹣A′O
2,
即:(7+x)2=
252﹣(24﹣a
)
2
18、如图所示,A、B两村在一条公路l的同侧,A、B两村到公路的距离分别为AC=3km,BD=5km,又CD=6km,为将A、B两村绿色农产品及时运出去,现要在公路l上建一货运中转站P,使P点到A、B两村的距离的和最短,请你在l上选择货运中转站P的位置,并求出最短距离.
解答:作出点A关于l的对称点,连接交l于点P,
连接AP,根据对称性可知,在点P处建货运中转站能使P
点到A、B两村的距离的和最短.
过点作∥l,交BD的延长线于点E,
∴=CD,=DE,
∵=
AC
=3km,BD=5km,CD=6km,
∴=CD=6km,BE=BD+DE=BD+=5+3=8(km),
在Rt△中,(km),
P点到A、B两村的距离最短为10
km.
21、(2019年四川巴中)如图,等腰直角三角板如图放置,直角顶点C在直线m上,分别过点A、B作AE⊥直线m于点E,BD⊥直线m于点D.
①求证:EC=BD.
②若设△AEC三边分别为a、b、c,
利用此图证明勾股定理.
解:①∵∠ACB=90°,∴∠ACE+∠BCD=90°.
∵BD⊥m,AE⊥m,∴∠CDB=90°,∠AEC=90°,
∴∠ACE+∠CAE=90°.∴∠CAE=∠BCD.
在△AEC和△CDB中,
∵∠AEC=∠CDB=90°,∠CAE=∠BCD,AC=CB,
∴△AEC≌△CDB(AAS),∴EC=BD.
②由①知BD=CE=a,CD=AE=b,∴S梯形ABDE=(a+b)(a+b)=a2+ab+b2.
又∵S梯形ABDE=S△AEC+
S△BCD+S△ABC=ab+ab+c2=ab+c2,
∴a2+ab+b2=ab+c2,∴a2+b2=c2.
即直角三角形两条直角边的平方和等于斜边的平方.
第11题图
第19题图
第20题图
第10题图
第8题图
第4题图
第22题图
第18题图
第1题图
第17题图
第22题图
第15题图
第3题图
第16题图
第8题图
例题2图
第7题图
例题2图
第16题图
例题1图2
第17题图
第16题图
第16题图
例题1图1
第18题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
