人教版八年级上册数学课件:11.3.2 多边形的内角和(共18张PPT)
文档属性
| 名称 | 人教版八年级上册数学课件:11.3.2 多边形的内角和(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 473.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-13 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
多边形的内角和
1.三角形的内角和是多少度?
2.如果两个三角形能够拼成四边形,你能求出四边形的内角和吗?
180°
360°
创设情境
温故探新
问题1
是否所有的四边形的内角和都可以“转化”为两个三角形的内角来求得呢?如何“转化”?
如图,在四边形ABCD中,连接对角线AC,则四边形ABCD被分成△ABC和△ACD两个三角形.
这种转化方法我们不妨称其为“对角线分割转化法”.
合作交流探究新知
问题2
类比推导四边形内角和的方法,你能推导出五边形和六边形的内角和各是多少吗?
观察上图填:(1)从五边形的一个顶点出发,可以作
条对角线,它们将五边形分为
个三角形,五边形的内角和等于180°×
.
(2)从六边形的一个顶点出发,可以作
条对角线,它们将六边形分为
个三角形,六边形的内角和等于180°×
.
2
3
3
3
4
4
问题3
n边形的内角和是否也可以用上面的方法?试一试.
一般地,从n边形的一个顶点出发,可以作(n-3)条对角线,它们将n边形分为(n-2)个三角形,n边形的内角和等于180
°×(n-2).
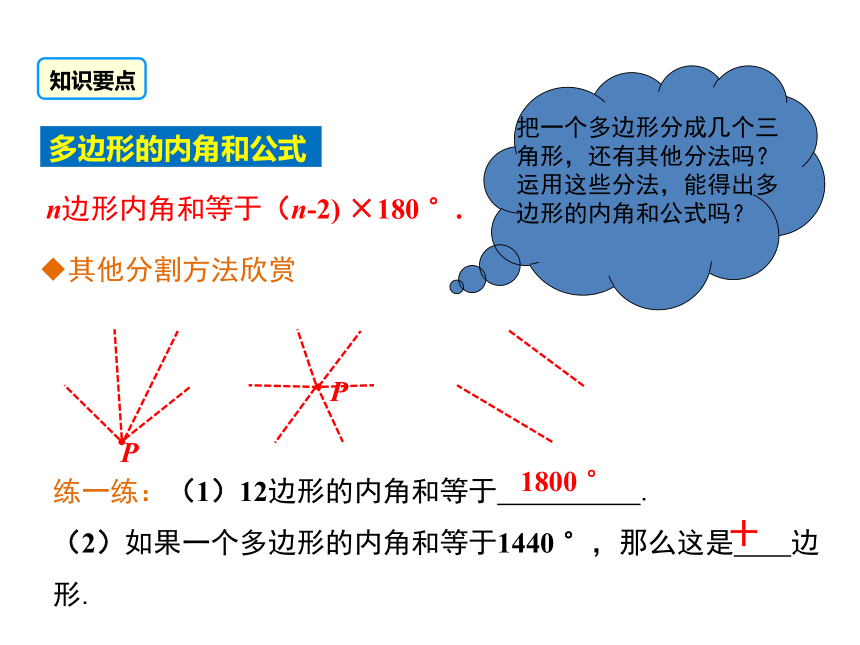
多边形的内角和公式
n边形内角和等于(n-2)
×180
°.
其他分割方法欣赏
练一练:(1)12边形的内角和等于
.
(2)如果一个多边形的内角和等于1440
°,那么这是
边形.
1800
°
十
P
P
想一想:如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
解:
如图,四边形ABCD中,∠A+
∠C
=180°.
∠A+∠B+∠C+∠D=(4-2)
×180
°=
360
°,
因为
∠B+∠D=
360°-(∠A+∠C)
=
360°-
180°
=180°.
所以
如果一个四边形的一组对角互补,那么另一组对角互补.
问题
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
互补
900°
五个平角和(900°)-五边形的内角和(540°)=外角和(360°)
五边形外角和
=360
°
=5个平角
-五边形内角和
=5×180°
-(5-2)
×
180°
结论:五边形的外角和等于360°.
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
n边形的外角和等于360°.
-(n-2)
×
180°
=360
°
=n个平角-n边形内角和
=
n×180
°
多边形的外角和公式
回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
练一练:(1)若一个正多边形的内角是120
°,那么这是正____边形.
(2)已知多边形的每个外角都是45°,则这个多边形是______边形.
六
正八
例1
已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解:
设多边形的边数为n.
∵它的内角和等于
(n-2)?180°,
多边形外角和等于360°,
∴
(n-2)?180°=2×
360?.
解得
n=6.
∴这个多边形的边数为6.
12
范例研讨运用新知
例2
已知一个多边形的每个内角与外角的比都是7:2,求这个多边形的边数.
解:设这个多边形的内角为7x
°,外角为2x°,根据题意得
7x+2x=180,
解得x=20.
即每个内角是140
°,每个外角是40
°.
360°
÷40
°=9.
答:这个多边形是九边形.
还有其他解法吗?
解:设这个多边形的边数为x
,根据题意得
解得x=9.
答:这个多边形是九边形.
1.判断.
(1)当多边形边数增加时,它的内角和也随着增加.
(
)
(2)当多边形边数增加时,它的外角和也随着增加.
(
)
(3)三角形的外角和与八边形的外角和相等.
(
)
(4)从n边形一个顶点出发,可以引出(n-2)条对角线,得到(n-2)个三角形.
(
)
2.五边形的内角和为
,它的对角线有
条.
540°
5
3.如果一个多边形的边数增加一条,那么这个多边形的内角和增加________,外角和增加_______.
180°
0°
反馈练习巩固新知
4.一个多边形的内角和不可能是(
)
A.1800°
B.540
°
C.720
°
D.810
°
D
5.一个多边形从一个顶点可引对角线3条,这个多边形内角和等于(
)
A.360°
B.540
°
C.720
°
D.900
°
D
能力提升:
一个多边形所有内角与一个外角的和是2380°,则这个多边形的边数为___.
15
解析:设这个多边形的边数为x(x为正整数),则这个多边形的内角和为(x-2)×180°,由题意可得:
2380-180<(x-2)×180°<2380,
解得:4.22因为x为正整数,所以x=15,即这个多边形的边数为13.
多边形的内角和
内角和计算公式
(n-2)
×
180
°(n
≥3的整数)
外角和
多边形的外角和等于360°
特别注意:与边数无关。
正多
边形
课堂小结
多边形的内角和
1.三角形的内角和是多少度?
2.如果两个三角形能够拼成四边形,你能求出四边形的内角和吗?
180°
360°
创设情境
温故探新
问题1
是否所有的四边形的内角和都可以“转化”为两个三角形的内角来求得呢?如何“转化”?
如图,在四边形ABCD中,连接对角线AC,则四边形ABCD被分成△ABC和△ACD两个三角形.
这种转化方法我们不妨称其为“对角线分割转化法”.
合作交流探究新知
问题2
类比推导四边形内角和的方法,你能推导出五边形和六边形的内角和各是多少吗?
观察上图填:(1)从五边形的一个顶点出发,可以作
条对角线,它们将五边形分为
个三角形,五边形的内角和等于180°×
.
(2)从六边形的一个顶点出发,可以作
条对角线,它们将六边形分为
个三角形,六边形的内角和等于180°×
.
2
3
3
3
4
4
问题3
n边形的内角和是否也可以用上面的方法?试一试.
一般地,从n边形的一个顶点出发,可以作(n-3)条对角线,它们将n边形分为(n-2)个三角形,n边形的内角和等于180
°×(n-2).
多边形的内角和公式
n边形内角和等于(n-2)
×180
°.
其他分割方法欣赏
练一练:(1)12边形的内角和等于
.
(2)如果一个多边形的内角和等于1440
°,那么这是
边形.
1800
°
十
P
P
想一想:如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
解:
如图,四边形ABCD中,∠A+
∠C
=180°.
∠A+∠B+∠C+∠D=(4-2)
×180
°=
360
°,
因为
∠B+∠D=
360°-(∠A+∠C)
=
360°-
180°
=180°.
所以
如果一个四边形的一组对角互补,那么另一组对角互补.
问题
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
互补
900°
五个平角和(900°)-五边形的内角和(540°)=外角和(360°)
五边形外角和
=360
°
=5个平角
-五边形内角和
=5×180°
-(5-2)
×
180°
结论:五边形的外角和等于360°.
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
n边形的外角和等于360°.
-(n-2)
×
180°
=360
°
=n个平角-n边形内角和
=
n×180
°
多边形的外角和公式
回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
练一练:(1)若一个正多边形的内角是120
°,那么这是正____边形.
(2)已知多边形的每个外角都是45°,则这个多边形是______边形.
六
正八
例1
已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解:
设多边形的边数为n.
∵它的内角和等于
(n-2)?180°,
多边形外角和等于360°,
∴
(n-2)?180°=2×
360?.
解得
n=6.
∴这个多边形的边数为6.
12
范例研讨运用新知
例2
已知一个多边形的每个内角与外角的比都是7:2,求这个多边形的边数.
解:设这个多边形的内角为7x
°,外角为2x°,根据题意得
7x+2x=180,
解得x=20.
即每个内角是140
°,每个外角是40
°.
360°
÷40
°=9.
答:这个多边形是九边形.
还有其他解法吗?
解:设这个多边形的边数为x
,根据题意得
解得x=9.
答:这个多边形是九边形.
1.判断.
(1)当多边形边数增加时,它的内角和也随着增加.
(
)
(2)当多边形边数增加时,它的外角和也随着增加.
(
)
(3)三角形的外角和与八边形的外角和相等.
(
)
(4)从n边形一个顶点出发,可以引出(n-2)条对角线,得到(n-2)个三角形.
(
)
2.五边形的内角和为
,它的对角线有
条.
540°
5
3.如果一个多边形的边数增加一条,那么这个多边形的内角和增加________,外角和增加_______.
180°
0°
反馈练习巩固新知
4.一个多边形的内角和不可能是(
)
A.1800°
B.540
°
C.720
°
D.810
°
D
5.一个多边形从一个顶点可引对角线3条,这个多边形内角和等于(
)
A.360°
B.540
°
C.720
°
D.900
°
D
能力提升:
一个多边形所有内角与一个外角的和是2380°,则这个多边形的边数为___.
15
解析:设这个多边形的边数为x(x为正整数),则这个多边形的内角和为(x-2)×180°,由题意可得:
2380-180<(x-2)×180°<2380,
解得:4.22
多边形的内角和
内角和计算公式
(n-2)
×
180
°(n
≥3的整数)
外角和
多边形的外角和等于360°
特别注意:与边数无关。
正多
边形
课堂小结
