五年级下册数学教案- 6.2.2 两步计算的分数除法问题 冀教版
文档属性
| 名称 | 五年级下册数学教案- 6.2.2 两步计算的分数除法问题 冀教版 |  | |
| 格式 | doc | ||
| 文件大小 | 93.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-13 07:33:04 | ||
图片预览

文档简介
《两步计算的分数除法问题》教学设计
一、教学内容
冀教版小学数学五年级下册第六单元《分数除法》第四课时(P78、79)
二、教材分析
本单元分数除法是在学生掌握了整数的四则运算和分数乘法、倒数的基础上学习的,除此之外,分数除法还与整数除法的意义、解方程有比较直接的关系。通过本单元的学习,学生能比较系统地掌握分数的四则运算,加深对乘除法关系的理解,体会数学知识间的内在联系,也为后面学习比和比例、百分数打下坚实的基础。
本节课内容是分数除法相关实际问题的第二课时——两步计算的分数除法问题。这类应用题历来是学生学习的难点。传统教学中,一般用算术方法解答分数除法问题:“已知部分和所对应的分率求整体,用除法。”这样无论如何也找不到学生能够理解和说明算理的数量关系,只能机械地“照葫芦画瓢”按照这一模式来计算,还经常因为单位“1”难以判断出现错误,既影响学生小学阶段的学习,而且还对学生升入初中后学习方程造成负面影响。所以教材首先抓住“求一个数的几分之几是多少用乘法”这一核心知识点,把单位“1”看做,找出题中的等量关系并列出方程,让学生掌握数量关系形如或的实际问题的解决方法,进一步让学生体会并掌握数学模型思想、方程思想,促进学生问题解决能力的发展。
三、学情分析
了解学生才能更好的因材施教。此时的学生具有整数四则运算、分数乘法、倒数、方程等知识储备,具有合情推理能力、借助图形分析问题能力、动手操作能力和一定的生活经验。
四、教学目标
1.结合具体事例,经历画线段图分析问题、列方程解答稍复杂的分数应用问题的过程;
2.能用方程解答稍复杂的分数应用问题,经历与他人交流的过程;
3.体会线段图在分析问题中的价值,获得用不同思路列方程解答分数应用问题的经验。
目标分解:
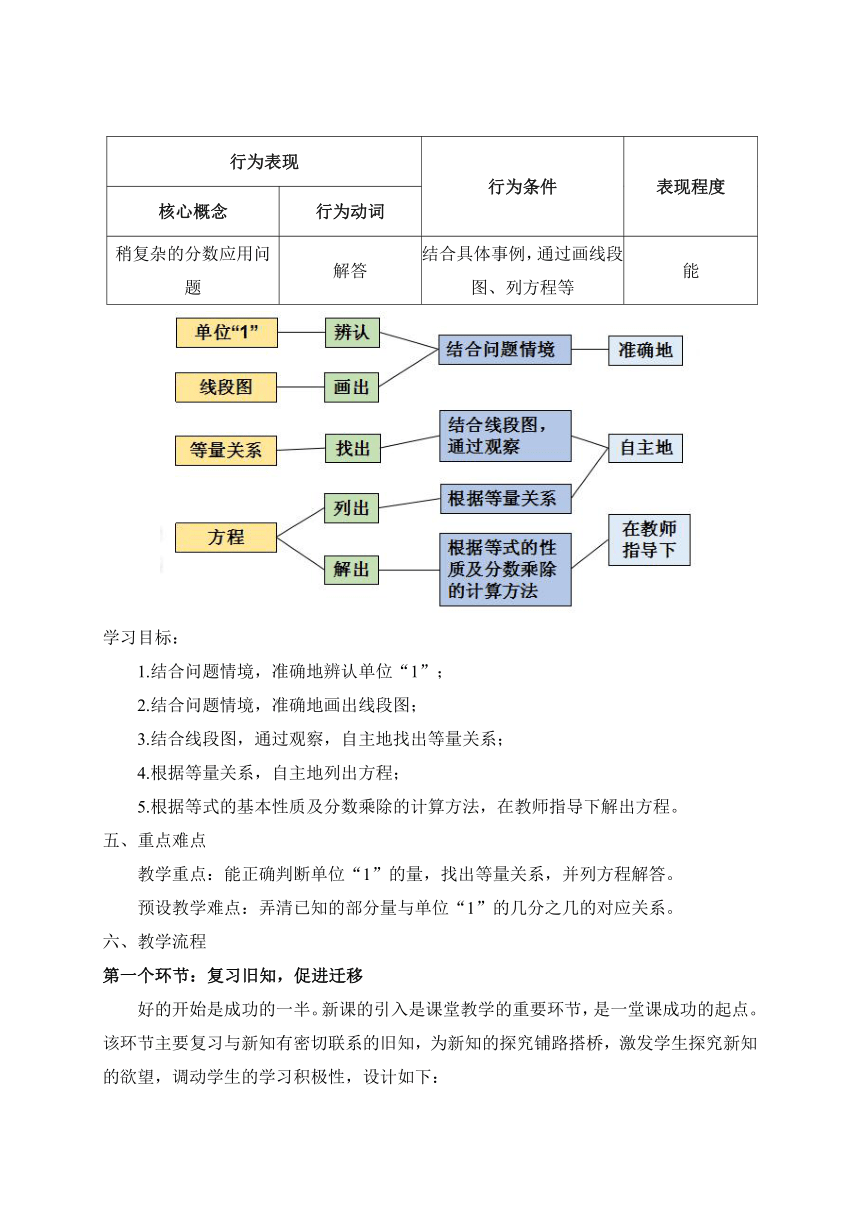
行为表现 行为条件 表现程度
核心概念 行为动词
稍复杂的分数应用问题 解答 结合具体事例,通过画线段图、列方程等 能
学习目标:
1.结合问题情境,准确地辨认单位“1”;
2.结合问题情境,准确地画出线段图;
3.结合线段图,通过观察,自主地找出等量关系;
4.根据等量关系,自主地列出方程;
5.根据等式的基本性质及分数乘除的计算方法,在教师指导下解出方程。
五、重点难点
教学重点:能正确判断单位“1”的量,找出等量关系,并列方程解答。
预设教学难点:弄清已知的部分量与单位“1”的几分之几的对应关系。
六、教学流程
第一个环节:复习旧知,促进迁移?
好的开始是成功的一半。新课的引入是课堂教学的重要环节,是一堂课成功的起点。该环节主要复习与新知有密切联系的旧知,为新知的探究铺路搭桥,激发学生探究新知的欲望,调动学生的学习积极性,设计如下:?
1.找出下面问题中的单位“1”。
(1)一本书已经看了 (2)一条绳子剪下一段后还剩
(3)实际比计划节约投资 (4)今年产量比去年提高
2.分数应用题练习
玩具厂计划为客户生产一批玩具车950辆,已经完成计划的,还剩多少辆没有完成?
(1)画图分析并列式解答。
(2)交流做法。
意图:本题是例题的一个变形,关键是找出单位“1”和题目中的等量关系,安排这一环节,一是回顾,二是为突破重点做好铺垫,因为这道题的数量关系与接下来例题的数量关系是完全相同的。
第二个环节:创设情境,探究新知?
出示例题:玩具厂计划为客户生产一批玩具车,已经完成计划的,还剩190辆没有完成,这批玩具车有多少辆?
对小学生来说,通过自己的探索获取新知,就是一种再创造,第二个环节的教学,设计如下五个层次展开:?
第一层次:比较异同
比较本题与上题的异同,通过比较学生会发现这里的等量关系不变,变的是其中的已知量与未知量,所以我们仍然可以顺着刚才的思路进行分析。
第二层次:独立探索?
思考以下几个问题,独立试做。
把哪个量看作单位“1”?怎样画出线段图?等量关系是什么?你想怎么做?
第三层次:合作探索?
在学生计算出结果后,组织学生分组合作,讨论交流是怎么做的?还有什么疑问??
第四层次:全班交流。在这一环节中,教师主要把握以下几点:
(1)凸显数形结合的思想,培养学生利用画图策略帮助思考的能力。指导学生画线段图时,引导学生思考单位1是谁,学生指出计划生产的玩具车总量就是单位1,所以先画出来,已经完成了计划的,而还要生产的190辆是未完成的,应占原计划的,于是190辆与原计划的建立了对应关系,这样边思考边把条件和问题简单明了地标注在图上,既突破难点:弄清已知的部分量与单位1的几分之几的对应关系,又清晰直观地把接下来要找的数量关系呈现出来。
(2)交流做法的多样性。在这里学生可能会出现两种做法,一种是方程法,一种是算术法。我们先看方程法,也是鼓励和提倡的。学生根据线段图找出两种等量关系:计划生产的-已经生产的=还要生产的,计划生产的×(1-)=还要生产的,根据不同的等量关系,列出两种不同的方程。在解方程的过程中,出现,无论学生想到方程两边同时除以,还是两边同时乘5,都是值得肯定的。在这个过程中,学生可能会根据等量关系推导出除法算式,也是可以的,但是我仍然认为方程是解决这类问题最重要的方法,这也是我想跟大家分享的第三点。
(3)列方程解决这类问题最大的优势在于思维的顺向性,通过线段图找出等量关系式,再把关系式中的数量分别用未知数和已知数代替,列出方程,学生会看到解决这一问题的思路与以前所学的乘法问题完全一致,感受方程解法的重要意义。
第五层次:检验结果。
既检验解答是否正确,又是对乘法数量关系的二次应用,也有助于学生养成严谨的数学态度。
第三个环节:变式练习,巩固深化
练习的设计要抓基础知识与发展创新能力紧密结合起来,以达到发展思维,形成技能的目标。在此环节我设计了如下练习:
让学生独立完成教材78页试一试(一个日用化工厂6月份生产洗衣皂9800箱,比原计划多生产3/7,这个日用化工厂原计划6月份生产洗衣皂多少箱?)
本题与例题类似,但已知的数量比单位“1”大,提示学生找出单位“1”,画出线段图,深入理解题里的等量关系,并列出方程解答,个别学生板演,教师在学生完成后集体点评。
第四个环节 课后作业,反馈信息
为了巩固所学知识,发展学生思维,在顺利完成了以上内容的教学之后,接下来我用两道作业题来反馈信息。
1、画出线段图,指出下列各题的“单位1”,并找出等量关系。以此来检验目标1、3的达成。
(1)一辆汽车从承德到北京,已行全程的3/4,此时距北京还有64千米,承德到北京有多少千米?
(2)学校去年上半年用电8640千瓦时,比下半年多用了1/8,去年下半年用电多少千瓦时?
2、小明的体重是35千克,他的体重比爸爸的体重轻8/15,小明爸爸的体重是多少千克?以此来检验目标1-5的达成效果。
一、教学内容
冀教版小学数学五年级下册第六单元《分数除法》第四课时(P78、79)
二、教材分析
本单元分数除法是在学生掌握了整数的四则运算和分数乘法、倒数的基础上学习的,除此之外,分数除法还与整数除法的意义、解方程有比较直接的关系。通过本单元的学习,学生能比较系统地掌握分数的四则运算,加深对乘除法关系的理解,体会数学知识间的内在联系,也为后面学习比和比例、百分数打下坚实的基础。
本节课内容是分数除法相关实际问题的第二课时——两步计算的分数除法问题。这类应用题历来是学生学习的难点。传统教学中,一般用算术方法解答分数除法问题:“已知部分和所对应的分率求整体,用除法。”这样无论如何也找不到学生能够理解和说明算理的数量关系,只能机械地“照葫芦画瓢”按照这一模式来计算,还经常因为单位“1”难以判断出现错误,既影响学生小学阶段的学习,而且还对学生升入初中后学习方程造成负面影响。所以教材首先抓住“求一个数的几分之几是多少用乘法”这一核心知识点,把单位“1”看做,找出题中的等量关系并列出方程,让学生掌握数量关系形如或的实际问题的解决方法,进一步让学生体会并掌握数学模型思想、方程思想,促进学生问题解决能力的发展。
三、学情分析
了解学生才能更好的因材施教。此时的学生具有整数四则运算、分数乘法、倒数、方程等知识储备,具有合情推理能力、借助图形分析问题能力、动手操作能力和一定的生活经验。
四、教学目标
1.结合具体事例,经历画线段图分析问题、列方程解答稍复杂的分数应用问题的过程;
2.能用方程解答稍复杂的分数应用问题,经历与他人交流的过程;
3.体会线段图在分析问题中的价值,获得用不同思路列方程解答分数应用问题的经验。
目标分解:
行为表现 行为条件 表现程度
核心概念 行为动词
稍复杂的分数应用问题 解答 结合具体事例,通过画线段图、列方程等 能
学习目标:
1.结合问题情境,准确地辨认单位“1”;
2.结合问题情境,准确地画出线段图;
3.结合线段图,通过观察,自主地找出等量关系;
4.根据等量关系,自主地列出方程;
5.根据等式的基本性质及分数乘除的计算方法,在教师指导下解出方程。
五、重点难点
教学重点:能正确判断单位“1”的量,找出等量关系,并列方程解答。
预设教学难点:弄清已知的部分量与单位“1”的几分之几的对应关系。
六、教学流程
第一个环节:复习旧知,促进迁移?
好的开始是成功的一半。新课的引入是课堂教学的重要环节,是一堂课成功的起点。该环节主要复习与新知有密切联系的旧知,为新知的探究铺路搭桥,激发学生探究新知的欲望,调动学生的学习积极性,设计如下:?
1.找出下面问题中的单位“1”。
(1)一本书已经看了 (2)一条绳子剪下一段后还剩
(3)实际比计划节约投资 (4)今年产量比去年提高
2.分数应用题练习
玩具厂计划为客户生产一批玩具车950辆,已经完成计划的,还剩多少辆没有完成?
(1)画图分析并列式解答。
(2)交流做法。
意图:本题是例题的一个变形,关键是找出单位“1”和题目中的等量关系,安排这一环节,一是回顾,二是为突破重点做好铺垫,因为这道题的数量关系与接下来例题的数量关系是完全相同的。
第二个环节:创设情境,探究新知?
出示例题:玩具厂计划为客户生产一批玩具车,已经完成计划的,还剩190辆没有完成,这批玩具车有多少辆?
对小学生来说,通过自己的探索获取新知,就是一种再创造,第二个环节的教学,设计如下五个层次展开:?
第一层次:比较异同
比较本题与上题的异同,通过比较学生会发现这里的等量关系不变,变的是其中的已知量与未知量,所以我们仍然可以顺着刚才的思路进行分析。
第二层次:独立探索?
思考以下几个问题,独立试做。
把哪个量看作单位“1”?怎样画出线段图?等量关系是什么?你想怎么做?
第三层次:合作探索?
在学生计算出结果后,组织学生分组合作,讨论交流是怎么做的?还有什么疑问??
第四层次:全班交流。在这一环节中,教师主要把握以下几点:
(1)凸显数形结合的思想,培养学生利用画图策略帮助思考的能力。指导学生画线段图时,引导学生思考单位1是谁,学生指出计划生产的玩具车总量就是单位1,所以先画出来,已经完成了计划的,而还要生产的190辆是未完成的,应占原计划的,于是190辆与原计划的建立了对应关系,这样边思考边把条件和问题简单明了地标注在图上,既突破难点:弄清已知的部分量与单位1的几分之几的对应关系,又清晰直观地把接下来要找的数量关系呈现出来。
(2)交流做法的多样性。在这里学生可能会出现两种做法,一种是方程法,一种是算术法。我们先看方程法,也是鼓励和提倡的。学生根据线段图找出两种等量关系:计划生产的-已经生产的=还要生产的,计划生产的×(1-)=还要生产的,根据不同的等量关系,列出两种不同的方程。在解方程的过程中,出现,无论学生想到方程两边同时除以,还是两边同时乘5,都是值得肯定的。在这个过程中,学生可能会根据等量关系推导出除法算式,也是可以的,但是我仍然认为方程是解决这类问题最重要的方法,这也是我想跟大家分享的第三点。
(3)列方程解决这类问题最大的优势在于思维的顺向性,通过线段图找出等量关系式,再把关系式中的数量分别用未知数和已知数代替,列出方程,学生会看到解决这一问题的思路与以前所学的乘法问题完全一致,感受方程解法的重要意义。
第五层次:检验结果。
既检验解答是否正确,又是对乘法数量关系的二次应用,也有助于学生养成严谨的数学态度。
第三个环节:变式练习,巩固深化
练习的设计要抓基础知识与发展创新能力紧密结合起来,以达到发展思维,形成技能的目标。在此环节我设计了如下练习:
让学生独立完成教材78页试一试(一个日用化工厂6月份生产洗衣皂9800箱,比原计划多生产3/7,这个日用化工厂原计划6月份生产洗衣皂多少箱?)
本题与例题类似,但已知的数量比单位“1”大,提示学生找出单位“1”,画出线段图,深入理解题里的等量关系,并列出方程解答,个别学生板演,教师在学生完成后集体点评。
第四个环节 课后作业,反馈信息
为了巩固所学知识,发展学生思维,在顺利完成了以上内容的教学之后,接下来我用两道作业题来反馈信息。
1、画出线段图,指出下列各题的“单位1”,并找出等量关系。以此来检验目标1、3的达成。
(1)一辆汽车从承德到北京,已行全程的3/4,此时距北京还有64千米,承德到北京有多少千米?
(2)学校去年上半年用电8640千瓦时,比下半年多用了1/8,去年下半年用电多少千瓦时?
2、小明的体重是35千克,他的体重比爸爸的体重轻8/15,小明爸爸的体重是多少千克?以此来检验目标1-5的达成效果。
