江苏省连云港市2019-2020学年高一下学期期末调研考试数学试题(word解析版)
文档属性
| 名称 | 江苏省连云港市2019-2020学年高一下学期期末调研考试数学试题(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 837.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-14 00:00:00 | ||
图片预览




文档简介
江苏省连云港市2019~2020学年第二学期高一年级期末调研考试
数学试题
2020.7
一、单项选择题(本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一个是符合题目要求的,请把答案添涂在答题卡相应位置上)
1.=
A.
B.
C.
D.
2.不等式的解集是
A.(,)
B.(,)(,)
C.(,)
D.(,)(,)
3.若从甲,乙,丙,丁4位同学中选出3名代表参加学校会议,则甲被选中的概率是
A.
B.
C.
D.
4.某校为了了解教科研工作开展状况与教师年龄
之间的关系,将该校不小于35岁的80名教师
按年龄分组,分组区间为[35,40),[40,45),
[45,50),[50,55),[55,60],由此得到频率
分布直方图如图,则这80名教师中年龄小于45
岁的人数有
第4题
A.45
B.46
C.48
D.50
5.过圆x2+y2=5上一点M(﹣1,2)作圆的切线l,则l的方程是
A.
B.
C.
D.
6.两条平行直线6x﹣4y+5=0与y=x的距离是
A.
B.
C.
D.
7.如图,在三棱锥S—ABC中,SB=SC=AB=AC=BC=4,SA
=,则异面直线SB与AC所成角的余弦值是
A.
B.
C.
D.
第7题
8.圆的圆心为C,直线l过点(0,3)且与圆C交于A,B两点,若△ABC的面积为,则满足条件的直线l的条数为
A.1
B.2
C.3
D.4
二、?多项选择题(本大题共4小题,每小题5分,?共计20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,请把答案添涂在答题卡相应位置上)
9.在4件产品中,有一等品2件,二等品1件(一等品与二等品都是正品),次品1件,现从中任取2件,则下列说法正确的是
A.两件都是一等品的概率是
B.两件中有1件是次品的概率是
C.两件都是正品的概率是
D.两件中至少有1件是一等品的概率是
10.关于异面直线a,b,下列四个命题正确的有
A.过直线a有且仅有一个平面,使b⊥
B.过直线a有且仅有一个平面,使b∥
C.在空间存在平面,使a∥,?b∥
D.在空间不存在平面,使a⊥,b⊥
11.正方体的外接球与内切球上各有一个动点M,N,若线段MN的最小值为,则
A.正方体的外接球的表面积为
B.正方体的内切球的体积为
C.正方体的棱长为1
D.线段MN的最大值为
12.瑞士著名数学家欧拉在1765?年提出定理:三角形的外心、重心、垂心位于同一直线上.这条直线被后人称为三角形的“欧拉线”.在平面直角坐标系中作△ABC,AB=AC=4,点B(﹣1,3),点C(4,﹣2),且其“欧拉线”与圆M:相切,则下列结论正确的是
A.圆M上点到直线x﹣y+3=0的最小距离为
B.圆M上点到直线x﹣y+3=0的最大距离为
C.若点(x,y)在圆M上,则x+y的最小值是3﹣
D.圆与圆M有公共点,则a取值范围是[,]
三、填空题(本大题共4小题,?每小题5分,共计20分.其中第16题共有2空,第一个空2分,第二个空3分;其余题均为一空,?每空5分.请把答案填写在答题卡相应位置上)
13.已知两点A(3,2),B(8,12),则直线AB的一般式方程为
.
14.用半圆形纸片卷成一个圆锥筒,该圆锥筒的高为,则半圆形纸片的半径为
.
15.设cosx=t,用t的代数式表示cos2x=
,用t的代数式表示cos3x=
.
16.在△ABC中,角A,B,C的对边分别为a,b,c,面积为S,且满足a2﹣(b﹣c)2=S,b+c=2,则S的最大值是
.
四、解答题(本大题共6小题,共计70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)
在△ABC中,角A,B,C的对边分别为a,b,c,若A=60°,b=1,S△ABC=.
(1)求c的值;
(2)求sinC的值.
18.(本小题满分12分)
已知tan(+)=,tan=﹣2.
(1)求tan;
(2)求sin2.
19.(本小题满分12分)
已知函数(其中aR).
(1)当a=﹣1时,解关于x的不等式;
(2)若的解集为R,求实数a的取值范围.
20.(本小题满分12分)
如图,在正方体ABCD—A1B1C1D1中,E为棱DD1的中点,求证:
(1)BD1∥平面EAC;
(2)平面EAC⊥平面AB1C.
21.(本小题满分12分)
在平面直角坐标系xOy中,圆C:x2+y2+4x﹣2ay+a2=0.
(1)若圆C与x轴相切,求实数a的值;
(2)若M,N为圆C上不同的两点,过点M,N分别作圆C的切线l1,l2,若l1与l2相交于点P,圆C上异于M,N另有一点Q,满足∠MQN=60°,若直线l:x﹣y﹣6=0上存在唯一的一个点T,使得,求实数a的值.
22.(本小题满分12分)
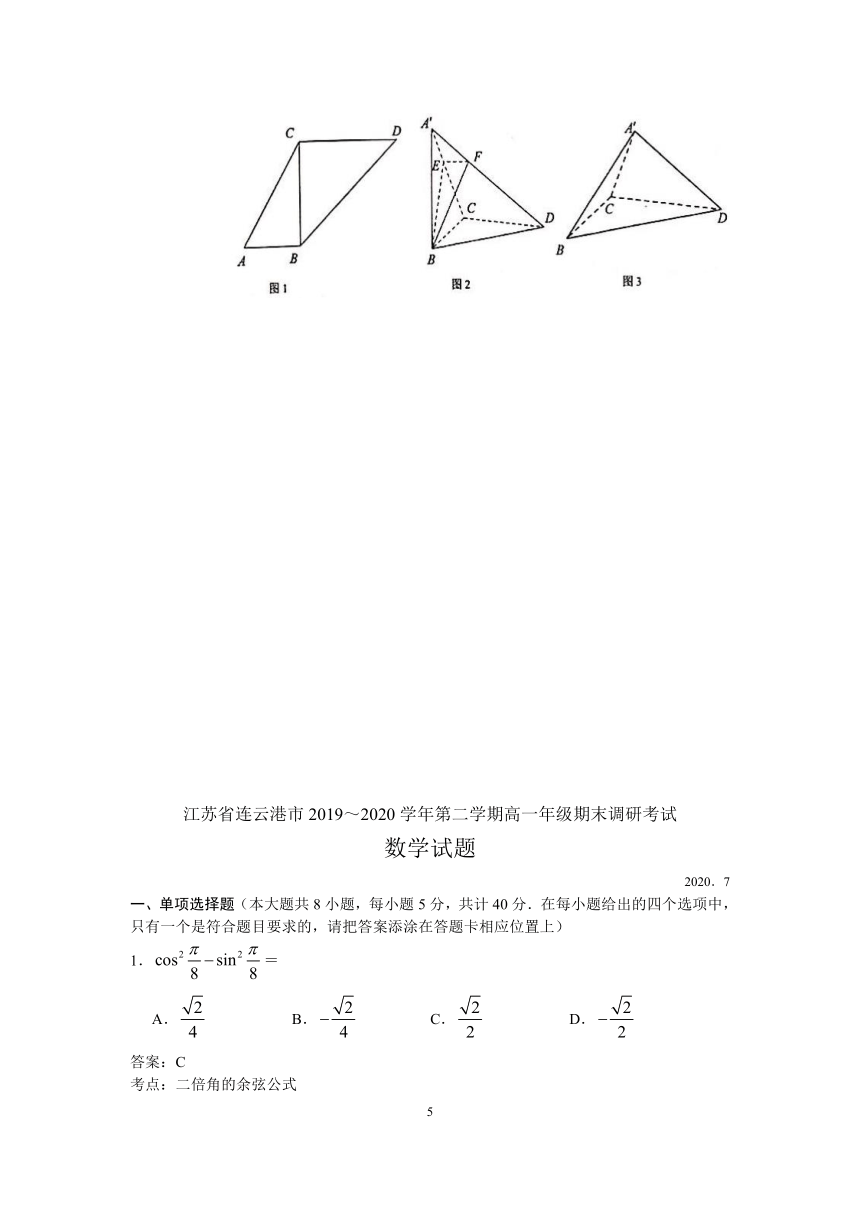
已知梯形ABCD中,AB=1,∠A=60°,∠ABC=90°,∠CBD=45°,如图(1)所示.现将△ABC沿边BC翻折至△A′BC,记二面角A′—BC—D的大小为.
(1)当=90°时,如图(2)所示,过点B作平面与A′D垂直,分别交A′C,A′D于点E,F,求点E到平面A′BF的距离;
(2)当=30°时,如图(3)所示,求二面角A′—CD—B的正切值.
江苏省连云港市2019~2020学年第二学期高一年级期末调研考试
数学试题
2020.7
一、单项选择题(本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一个是符合题目要求的,请把答案添涂在答题卡相应位置上)
1.=
A.
B.
C.
D.
答案:C
考点:二倍角的余弦公式
解析:,故选C.
2.不等式的解集是
A.(,)
B.(,)(,)
C.(,)
D.(,)(,)
答案:B
考点:一元二次不等式
解析:∵,∴或,故选B.
3.若从甲,乙,丙,丁4位同学中选出3名代表参加学校会议,则甲被选中的概率是
A.
B.
C.
D.
答案:D
考点:古典概型
解析:P=,故选D.
4.某校为了了解教科研工作开展状况与教师年龄
之间的关系,将该校不小于35岁的80名教师
按年龄分组,分组区间为[35,40),[40,45),
[45,50),[50,55),[55,60],由此得到频率
分布直方图如图,则这80名教师中年龄小于45
岁的人数有
第4题
A.45
B.46
C.48
D.50
答案:C
考点:频率分布直方图
解析:,故选C.
5.过圆x2+y2=5上一点M(﹣1,2)作圆的切线l,则l的方程是
A.
B.
C.
D.
答案:B
考点:圆的切线方程
解析:根据切线方程公式可得切线方程为,即,故选B.
6.两条平行直线6x﹣4y+5=0与y=x的距离是
A.
B.
C.
D.
答案:D
考点:两平行直线间的距离公式
解析:根据两平行间的距离公式可得,故选D.
7.如图,在三棱锥S—ABC中,SB=SC=AB=AC=BC=4,SA
=,则异面直线SB与AC所成角的余弦值是
A.
B.
C.
D.
第7题
答案:A
考点:异面直线所成的角
解析:取AB、BC、SC、SA的中点分别为D、E、F、G,
则∠EFG就是异面直线SB与AC所成的角或补角,
首先可判断出三角形SAE是等边三角形,求得三角形SAE高EG=3,
FG=FE=2,
所以,
故异面直线SB与AC所成角的余弦值是,故选A.
8.圆的圆心为C,直线l过点(0,3)且与圆C交于A,B两点,若△ABC的面积为,则满足条件的直线l的条数为
A.1
B.2
C.3
D.4
答案:D
考点:直线与圆相交
解析:圆化为标准方程为,
则,∴∠ACB=60°或120°,
故圆心到直线AB的距离为1或,当l斜率不存在时,符合题意,
当l斜率为k时,设直线为,1或,
解得k=,或,综上所述,共有4条,故选D.
二、?多项选择题(本大题共4小题,每小题5分,?共计20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,请把答案添涂在答题卡相应位置上)
9.在4件产品中,有一等品2件,二等品1件(一等品与二等品都是正品),次品1件,现从中任取2件,则下列说法正确的是
A.两件都是一等品的概率是
B.两件中有1件是次品的概率是
C.两件都是正品的概率是
D.两件中至少有1件是一等品的概率是
答案:BD
考点:几何概型
解析:两件都是一等品的概率,故A错误;两件中有1件是次品的概率为,故B正确;
两件都是正品的概率是,故C错误;两件中至少有1件是一等品的概率是,故D正确.故选BD.
10.关于异面直线a,b,下列四个命题正确的有
A.过直线a有且仅有一个平面,使b⊥
B.过直线a有且仅有一个平面,使b∥
C.在空间存在平面,使a∥,?b∥
D.在空间不存在平面,使a⊥,b⊥
答案:BCD
考点:空间中的位置关系
解析:当直线a⊥b,过直线a有无数个平面,能使b⊥,故A错误;
异面直线a,b,过直线a有且仅有一个平面,使b∥,故B正确;
异面直线a,b,在空间存在平面,使a∥,?b∥,故C正确;
如果a⊥,b⊥,则a∥b,即直线a,b共面,反之异面直线a,b,在空间不存在平面,使a⊥,b⊥故D正确.故选BCD.
11.正方体的外接球与内切球上各有一个动点M,N,若线段MN的最小值为,则
A.正方体的外接球的表面积为
B.正方体的内切球的体积为
C.正方体的棱长为1
D.线段MN的最大值为
答案:AD
考点:正方体的外接球与内切球
解析:设正方体棱长为a,则,解得a=2,
正方体外接球半径为,内切球半径为1,
正方体外接球表面积为,故A正确;
内切球体积为,故B错误;
正方体的棱长为2,故C错误;
线段MN的最大值为,故D正确.故选AD.
12.瑞士著名数学家欧拉在1765?年提出定理:三角形的外心、重心、垂心位于同一直线上.这条直线被后人称为三角形的“欧拉线”.在平面直角坐标系中作△ABC,AB=AC=4,点B(﹣1,3),点C(4,﹣2),且其“欧拉线”与圆M:相切,则下列结论正确的是
A.圆M上点到直线x﹣y+3=0的最小距离为
B.圆M上点到直线x﹣y+3=0的最大距离为
C.若点(x,y)在圆M上,则x+y的最小值是3﹣
D.圆与圆M有公共点,则a取值范围是[,]
答案:ACD
考点:与圆有关的位置关系
解析:取BC中点D(,),,,故直线AD为x﹣y﹣1=0,
故,求得圆心M到直线x﹣y+3=0的距离为,
故圆M上点到直线x﹣y+3=0的最小距离为,最大距离为,所以A正确,B错误;
设,,则
,
则x+y的最小值是3﹣,故C正确;
,解得,故D正确.故选ACD.
三、填空题(本大题共4小题,?每小题5分,共计20分.其中第16题共有2空,第一个空2分,第二个空3分;其余题均为一空,?每空5分.请把答案填写在答题卡相应位置上)
13.已知两点A(3,2),B(8,12),则直线AB的一般式方程为
.
答案:
考点:直线的两点式、一般式
解析:,化为一般式为.
14.用半圆形纸片卷成一个圆锥筒,该圆锥筒的高为,则半圆形纸片的半径为
.
答案:2
考点:圆锥的侧面展开图
解析:半圆形纸片做成的圆锥,母线是底面半径的2倍,由于圆锥筒的高为,故半圆形纸片的半径为2.
15.设cosx=t,用t的代数式表示cos2x=
,用t的代数式表示cos3x=
.
答案:,
考点:三角恒等变换
解析:,
.
16.在△ABC中,角A,B,C的对边分别为a,b,c,面积为S,且满足a2﹣(b﹣c)2=S,b+c=2,则S的最大值是
.
答案:
考点:余弦定理,解三角形
解析:,
化简得,又,
解得(舍),或,则,
,
当b=1时,S有最大值为.
四、解答题(本大题共6小题,共计70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)
在△ABC中,角A,B,C的对边分别为a,b,c,若A=60°,b=1,S△ABC=.
(1)求c的值;
(2)求sinC的值.
解:(1)在中,,
所以,所以;
(2)在中,由余弦定理得:
所以,所以,
在中,由正弦定理得:,
所以.
18.(本小题满分12分)
已知tan(+)=,tan=﹣2.
(1)求tan;
(2)求sin2.
解:(1),
因为,,所以
(2),
因为,所以
19.(本小题满分12分)
已知函数(其中aR).
(1)当a=﹣1时,解关于x的不等式;
(2)若的解集为R,求实数a的取值范围.
解:(1)当时,由得,,
所以,所以不等式的解集为;
(2)因为解集为,所以在恒成立,
当时,得,不合题意;
当时,由在恒成立,
得,
所以
20.(本小题满分12分)
如图,在正方体ABCD—A1B1C1D1中,E为棱DD1的中点,求证:
(1)BD1∥平面EAC;
(2)平面EAC⊥平面AB1C.
证明:(1)连接BD交AC与O,连接OE,
因为O是BD中点,是棱的中点,
所以OE∥BD1,又BD1平面,OE?平面,
所以∥平面;
(2)方法一:连接,设正方体边长为1
在△中,,是中点,得,同理,故为所成二面角的平面角,
在△中,,,
得
故
故平面平面
法二:连接,在正方体中,
面,面,得
是正方形,得,又,
得面,面,故
∥得,
在△中,,是中点,得
又,得面,平面
故平面平面.
21.(本小题满分12分)
在平面直角坐标系xOy中,圆C:x2+y2+4x﹣2ay+a2=0.
(1)若圆C与x轴相切,求实数a的值;
(2)若M,N为圆C上不同的两点,过点M,N分别作圆C的切线l1,l2,若l1与l2相交于点P,圆C上异于M,N另有一点Q,满足∠MQN=60°,若直线l:x﹣y﹣6=0上存在唯一的一个点T,使得,求实数a的值.
解:(1)圆的方程可以化为:,
所以圆心,半径为2,
因为圆与轴相切,所以,所以
(2)因为点在圆上,且,
所以,
因为分别是圆的切线,
所以,即点在以为圆心,为半径的圆上,
所以点的轨迹方程为,
设,,
由得,
所以,即,所以,
因为直线上一存在唯一点,使得,
所以只有一组解,
所以,所以
22.(本小题满分12分)
已知梯形ABCD中,AB=1,∠A=60°,∠ABC=90°,∠CBD=45°,如图(1)所示.现将△ABC沿边BC翻折至△A′BC,记二面角A′—BC—D的大小为.
(1)当=90°时,如图(2)所示,过点B作平面与A′D垂直,分别交A′C,A′D于点E,F,求点E到平面A′BF的距离;
(2)当=30°时,如图(3)所示,求二面角A′—CD—B的正切值.
解:(1)因为平面平面,平面平面,
,平面,
所以平面,又平面,所以,
因为,,所以
又,,
所以,又,所以,
在中,,
又,,,
所以,又,所以,
在中,,所以,
在中,,
设点到平面的距离为,因为,所以,
所以;
(2)过点作直线//,过作交于点.因为,所以,又因为,所以就是二面角的平面角,
所以,因为,所以,
过点作交于点,连接,
因为,,,所以,
又,所以
又因为,,
所以,
因为,所以,
因为,所以,
所以是二面角的平面角,
在中,,
所以二面角的正切值为.
2
数学试题
2020.7
一、单项选择题(本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一个是符合题目要求的,请把答案添涂在答题卡相应位置上)
1.=
A.
B.
C.
D.
2.不等式的解集是
A.(,)
B.(,)(,)
C.(,)
D.(,)(,)
3.若从甲,乙,丙,丁4位同学中选出3名代表参加学校会议,则甲被选中的概率是
A.
B.
C.
D.
4.某校为了了解教科研工作开展状况与教师年龄
之间的关系,将该校不小于35岁的80名教师
按年龄分组,分组区间为[35,40),[40,45),
[45,50),[50,55),[55,60],由此得到频率
分布直方图如图,则这80名教师中年龄小于45
岁的人数有
第4题
A.45
B.46
C.48
D.50
5.过圆x2+y2=5上一点M(﹣1,2)作圆的切线l,则l的方程是
A.
B.
C.
D.
6.两条平行直线6x﹣4y+5=0与y=x的距离是
A.
B.
C.
D.
7.如图,在三棱锥S—ABC中,SB=SC=AB=AC=BC=4,SA
=,则异面直线SB与AC所成角的余弦值是
A.
B.
C.
D.
第7题
8.圆的圆心为C,直线l过点(0,3)且与圆C交于A,B两点,若△ABC的面积为,则满足条件的直线l的条数为
A.1
B.2
C.3
D.4
二、?多项选择题(本大题共4小题,每小题5分,?共计20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,请把答案添涂在答题卡相应位置上)
9.在4件产品中,有一等品2件,二等品1件(一等品与二等品都是正品),次品1件,现从中任取2件,则下列说法正确的是
A.两件都是一等品的概率是
B.两件中有1件是次品的概率是
C.两件都是正品的概率是
D.两件中至少有1件是一等品的概率是
10.关于异面直线a,b,下列四个命题正确的有
A.过直线a有且仅有一个平面,使b⊥
B.过直线a有且仅有一个平面,使b∥
C.在空间存在平面,使a∥,?b∥
D.在空间不存在平面,使a⊥,b⊥
11.正方体的外接球与内切球上各有一个动点M,N,若线段MN的最小值为,则
A.正方体的外接球的表面积为
B.正方体的内切球的体积为
C.正方体的棱长为1
D.线段MN的最大值为
12.瑞士著名数学家欧拉在1765?年提出定理:三角形的外心、重心、垂心位于同一直线上.这条直线被后人称为三角形的“欧拉线”.在平面直角坐标系中作△ABC,AB=AC=4,点B(﹣1,3),点C(4,﹣2),且其“欧拉线”与圆M:相切,则下列结论正确的是
A.圆M上点到直线x﹣y+3=0的最小距离为
B.圆M上点到直线x﹣y+3=0的最大距离为
C.若点(x,y)在圆M上,则x+y的最小值是3﹣
D.圆与圆M有公共点,则a取值范围是[,]
三、填空题(本大题共4小题,?每小题5分,共计20分.其中第16题共有2空,第一个空2分,第二个空3分;其余题均为一空,?每空5分.请把答案填写在答题卡相应位置上)
13.已知两点A(3,2),B(8,12),则直线AB的一般式方程为
.
14.用半圆形纸片卷成一个圆锥筒,该圆锥筒的高为,则半圆形纸片的半径为
.
15.设cosx=t,用t的代数式表示cos2x=
,用t的代数式表示cos3x=
.
16.在△ABC中,角A,B,C的对边分别为a,b,c,面积为S,且满足a2﹣(b﹣c)2=S,b+c=2,则S的最大值是
.
四、解答题(本大题共6小题,共计70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)
在△ABC中,角A,B,C的对边分别为a,b,c,若A=60°,b=1,S△ABC=.
(1)求c的值;
(2)求sinC的值.
18.(本小题满分12分)
已知tan(+)=,tan=﹣2.
(1)求tan;
(2)求sin2.
19.(本小题满分12分)
已知函数(其中aR).
(1)当a=﹣1时,解关于x的不等式;
(2)若的解集为R,求实数a的取值范围.
20.(本小题满分12分)
如图,在正方体ABCD—A1B1C1D1中,E为棱DD1的中点,求证:
(1)BD1∥平面EAC;
(2)平面EAC⊥平面AB1C.
21.(本小题满分12分)
在平面直角坐标系xOy中,圆C:x2+y2+4x﹣2ay+a2=0.
(1)若圆C与x轴相切,求实数a的值;
(2)若M,N为圆C上不同的两点,过点M,N分别作圆C的切线l1,l2,若l1与l2相交于点P,圆C上异于M,N另有一点Q,满足∠MQN=60°,若直线l:x﹣y﹣6=0上存在唯一的一个点T,使得,求实数a的值.
22.(本小题满分12分)
已知梯形ABCD中,AB=1,∠A=60°,∠ABC=90°,∠CBD=45°,如图(1)所示.现将△ABC沿边BC翻折至△A′BC,记二面角A′—BC—D的大小为.
(1)当=90°时,如图(2)所示,过点B作平面与A′D垂直,分别交A′C,A′D于点E,F,求点E到平面A′BF的距离;
(2)当=30°时,如图(3)所示,求二面角A′—CD—B的正切值.
江苏省连云港市2019~2020学年第二学期高一年级期末调研考试
数学试题
2020.7
一、单项选择题(本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一个是符合题目要求的,请把答案添涂在答题卡相应位置上)
1.=
A.
B.
C.
D.
答案:C
考点:二倍角的余弦公式
解析:,故选C.
2.不等式的解集是
A.(,)
B.(,)(,)
C.(,)
D.(,)(,)
答案:B
考点:一元二次不等式
解析:∵,∴或,故选B.
3.若从甲,乙,丙,丁4位同学中选出3名代表参加学校会议,则甲被选中的概率是
A.
B.
C.
D.
答案:D
考点:古典概型
解析:P=,故选D.
4.某校为了了解教科研工作开展状况与教师年龄
之间的关系,将该校不小于35岁的80名教师
按年龄分组,分组区间为[35,40),[40,45),
[45,50),[50,55),[55,60],由此得到频率
分布直方图如图,则这80名教师中年龄小于45
岁的人数有
第4题
A.45
B.46
C.48
D.50
答案:C
考点:频率分布直方图
解析:,故选C.
5.过圆x2+y2=5上一点M(﹣1,2)作圆的切线l,则l的方程是
A.
B.
C.
D.
答案:B
考点:圆的切线方程
解析:根据切线方程公式可得切线方程为,即,故选B.
6.两条平行直线6x﹣4y+5=0与y=x的距离是
A.
B.
C.
D.
答案:D
考点:两平行直线间的距离公式
解析:根据两平行间的距离公式可得,故选D.
7.如图,在三棱锥S—ABC中,SB=SC=AB=AC=BC=4,SA
=,则异面直线SB与AC所成角的余弦值是
A.
B.
C.
D.
第7题
答案:A
考点:异面直线所成的角
解析:取AB、BC、SC、SA的中点分别为D、E、F、G,
则∠EFG就是异面直线SB与AC所成的角或补角,
首先可判断出三角形SAE是等边三角形,求得三角形SAE高EG=3,
FG=FE=2,
所以,
故异面直线SB与AC所成角的余弦值是,故选A.
8.圆的圆心为C,直线l过点(0,3)且与圆C交于A,B两点,若△ABC的面积为,则满足条件的直线l的条数为
A.1
B.2
C.3
D.4
答案:D
考点:直线与圆相交
解析:圆化为标准方程为,
则,∴∠ACB=60°或120°,
故圆心到直线AB的距离为1或,当l斜率不存在时,符合题意,
当l斜率为k时,设直线为,1或,
解得k=,或,综上所述,共有4条,故选D.
二、?多项选择题(本大题共4小题,每小题5分,?共计20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,请把答案添涂在答题卡相应位置上)
9.在4件产品中,有一等品2件,二等品1件(一等品与二等品都是正品),次品1件,现从中任取2件,则下列说法正确的是
A.两件都是一等品的概率是
B.两件中有1件是次品的概率是
C.两件都是正品的概率是
D.两件中至少有1件是一等品的概率是
答案:BD
考点:几何概型
解析:两件都是一等品的概率,故A错误;两件中有1件是次品的概率为,故B正确;
两件都是正品的概率是,故C错误;两件中至少有1件是一等品的概率是,故D正确.故选BD.
10.关于异面直线a,b,下列四个命题正确的有
A.过直线a有且仅有一个平面,使b⊥
B.过直线a有且仅有一个平面,使b∥
C.在空间存在平面,使a∥,?b∥
D.在空间不存在平面,使a⊥,b⊥
答案:BCD
考点:空间中的位置关系
解析:当直线a⊥b,过直线a有无数个平面,能使b⊥,故A错误;
异面直线a,b,过直线a有且仅有一个平面,使b∥,故B正确;
异面直线a,b,在空间存在平面,使a∥,?b∥,故C正确;
如果a⊥,b⊥,则a∥b,即直线a,b共面,反之异面直线a,b,在空间不存在平面,使a⊥,b⊥故D正确.故选BCD.
11.正方体的外接球与内切球上各有一个动点M,N,若线段MN的最小值为,则
A.正方体的外接球的表面积为
B.正方体的内切球的体积为
C.正方体的棱长为1
D.线段MN的最大值为
答案:AD
考点:正方体的外接球与内切球
解析:设正方体棱长为a,则,解得a=2,
正方体外接球半径为,内切球半径为1,
正方体外接球表面积为,故A正确;
内切球体积为,故B错误;
正方体的棱长为2,故C错误;
线段MN的最大值为,故D正确.故选AD.
12.瑞士著名数学家欧拉在1765?年提出定理:三角形的外心、重心、垂心位于同一直线上.这条直线被后人称为三角形的“欧拉线”.在平面直角坐标系中作△ABC,AB=AC=4,点B(﹣1,3),点C(4,﹣2),且其“欧拉线”与圆M:相切,则下列结论正确的是
A.圆M上点到直线x﹣y+3=0的最小距离为
B.圆M上点到直线x﹣y+3=0的最大距离为
C.若点(x,y)在圆M上,则x+y的最小值是3﹣
D.圆与圆M有公共点,则a取值范围是[,]
答案:ACD
考点:与圆有关的位置关系
解析:取BC中点D(,),,,故直线AD为x﹣y﹣1=0,
故,求得圆心M到直线x﹣y+3=0的距离为,
故圆M上点到直线x﹣y+3=0的最小距离为,最大距离为,所以A正确,B错误;
设,,则
,
则x+y的最小值是3﹣,故C正确;
,解得,故D正确.故选ACD.
三、填空题(本大题共4小题,?每小题5分,共计20分.其中第16题共有2空,第一个空2分,第二个空3分;其余题均为一空,?每空5分.请把答案填写在答题卡相应位置上)
13.已知两点A(3,2),B(8,12),则直线AB的一般式方程为
.
答案:
考点:直线的两点式、一般式
解析:,化为一般式为.
14.用半圆形纸片卷成一个圆锥筒,该圆锥筒的高为,则半圆形纸片的半径为
.
答案:2
考点:圆锥的侧面展开图
解析:半圆形纸片做成的圆锥,母线是底面半径的2倍,由于圆锥筒的高为,故半圆形纸片的半径为2.
15.设cosx=t,用t的代数式表示cos2x=
,用t的代数式表示cos3x=
.
答案:,
考点:三角恒等变换
解析:,
.
16.在△ABC中,角A,B,C的对边分别为a,b,c,面积为S,且满足a2﹣(b﹣c)2=S,b+c=2,则S的最大值是
.
答案:
考点:余弦定理,解三角形
解析:,
化简得,又,
解得(舍),或,则,
,
当b=1时,S有最大值为.
四、解答题(本大题共6小题,共计70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)
在△ABC中,角A,B,C的对边分别为a,b,c,若A=60°,b=1,S△ABC=.
(1)求c的值;
(2)求sinC的值.
解:(1)在中,,
所以,所以;
(2)在中,由余弦定理得:
所以,所以,
在中,由正弦定理得:,
所以.
18.(本小题满分12分)
已知tan(+)=,tan=﹣2.
(1)求tan;
(2)求sin2.
解:(1),
因为,,所以
(2),
因为,所以
19.(本小题满分12分)
已知函数(其中aR).
(1)当a=﹣1时,解关于x的不等式;
(2)若的解集为R,求实数a的取值范围.
解:(1)当时,由得,,
所以,所以不等式的解集为;
(2)因为解集为,所以在恒成立,
当时,得,不合题意;
当时,由在恒成立,
得,
所以
20.(本小题满分12分)
如图,在正方体ABCD—A1B1C1D1中,E为棱DD1的中点,求证:
(1)BD1∥平面EAC;
(2)平面EAC⊥平面AB1C.
证明:(1)连接BD交AC与O,连接OE,
因为O是BD中点,是棱的中点,
所以OE∥BD1,又BD1平面,OE?平面,
所以∥平面;
(2)方法一:连接,设正方体边长为1
在△中,,是中点,得,同理,故为所成二面角的平面角,
在△中,,,
得
故
故平面平面
法二:连接,在正方体中,
面,面,得
是正方形,得,又,
得面,面,故
∥得,
在△中,,是中点,得
又,得面,平面
故平面平面.
21.(本小题满分12分)
在平面直角坐标系xOy中,圆C:x2+y2+4x﹣2ay+a2=0.
(1)若圆C与x轴相切,求实数a的值;
(2)若M,N为圆C上不同的两点,过点M,N分别作圆C的切线l1,l2,若l1与l2相交于点P,圆C上异于M,N另有一点Q,满足∠MQN=60°,若直线l:x﹣y﹣6=0上存在唯一的一个点T,使得,求实数a的值.
解:(1)圆的方程可以化为:,
所以圆心,半径为2,
因为圆与轴相切,所以,所以
(2)因为点在圆上,且,
所以,
因为分别是圆的切线,
所以,即点在以为圆心,为半径的圆上,
所以点的轨迹方程为,
设,,
由得,
所以,即,所以,
因为直线上一存在唯一点,使得,
所以只有一组解,
所以,所以
22.(本小题满分12分)
已知梯形ABCD中,AB=1,∠A=60°,∠ABC=90°,∠CBD=45°,如图(1)所示.现将△ABC沿边BC翻折至△A′BC,记二面角A′—BC—D的大小为.
(1)当=90°时,如图(2)所示,过点B作平面与A′D垂直,分别交A′C,A′D于点E,F,求点E到平面A′BF的距离;
(2)当=30°时,如图(3)所示,求二面角A′—CD—B的正切值.
解:(1)因为平面平面,平面平面,
,平面,
所以平面,又平面,所以,
因为,,所以
又,,
所以,又,所以,
在中,,
又,,,
所以,又,所以,
在中,,所以,
在中,,
设点到平面的距离为,因为,所以,
所以;
(2)过点作直线//,过作交于点.因为,所以,又因为,所以就是二面角的平面角,
所以,因为,所以,
过点作交于点,连接,
因为,,,所以,
又,所以
又因为,,
所以,
因为,所以,
因为,所以,
所以是二面角的平面角,
在中,,
所以二面角的正切值为.
2
同课章节目录
