冀教版数学九年级上册 25.3 相似三角形 课件 (共19张PPT)
文档属性
| 名称 | 冀教版数学九年级上册 25.3 相似三角形 课件 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 282.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-13 14:41:30 | ||
图片预览



文档简介
(共19张PPT)
25.3.1
相似三角形
蓦然回首
1、什么叫做全等三角形?
能够完全重合的两个三角形叫做全等三角形.
(如右图△ABC≌DEF)
2、全等三角形的对应边、对应角之间各有什么关系?
性质:对应边相等、对应角相等.
A
B
C
D
E
F
1
探究新知
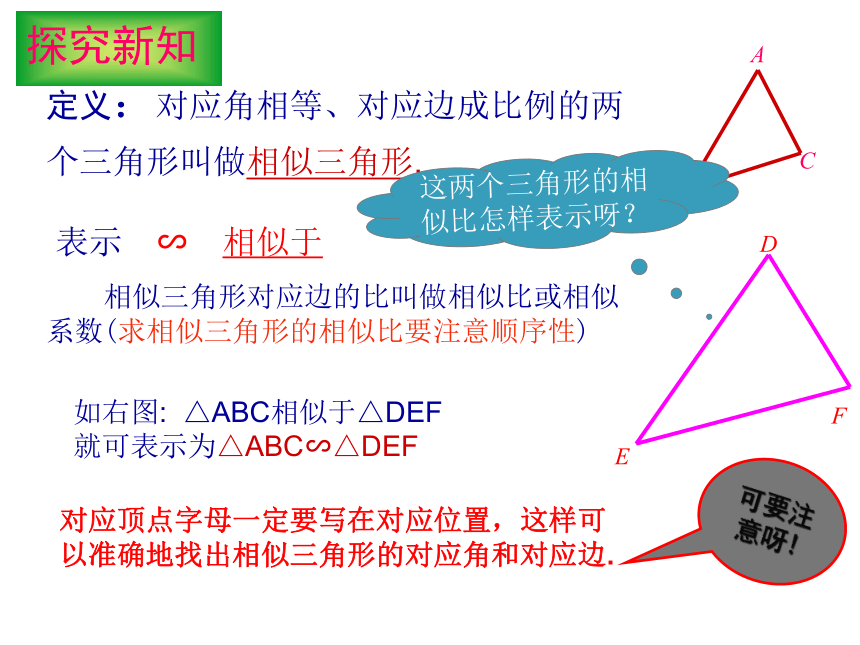
定义:对应角相等、对应边成比例的两个三角形叫做相似三角形.
A
B
C
E
D
F
表示:∽,相似于”
如右图:
△ABC相似于△DEF
就可表示为△ABC∽△DEF
对应顶点字母一定要写在对应位置,这样可以准确地找出相似三角形的对应角和对应边.
可要注意呀!
相似相似三角形对应边的比叫做相似比或相似系数(求相似三角形的相似比要注意顺序性)
这两个三角形的相似比怎样表示呀?
想一想
对应角相等、对应边成比例
相似三角形具有传递性
A
B
C
D
E
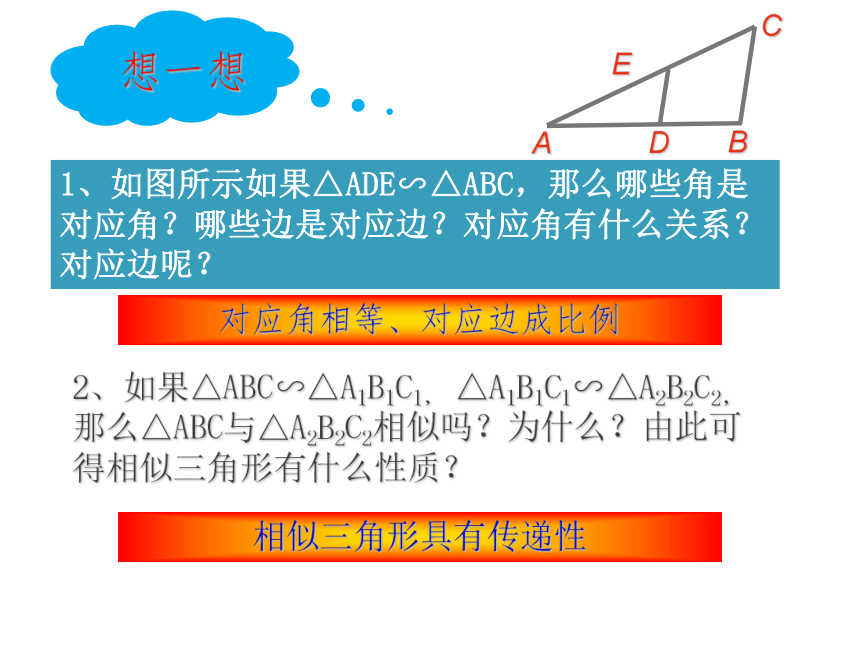
1、如图所示如果△ADE∽△ABC,那么哪些角是对应角?哪些边是对应边?对应角有什么关系?对应边呢?
2、如果△ABC∽△A1B1C1,
△A1B1C1∽△A2B2C2,那么△ABC与△A2B2C2相似吗?为什么?由此可得相似三角形有什么性质?
【1】两个全等三角形一定相似吗?为什么?它与相似三角形有什么关系?
两个全等三角形的对应边相等,对应角相等,由对应边相等可知对应边一定成比例,且相似比为1,因此满足相似三角形的两个条件,所以两个全等三角形一定相似.全等三角形是相似三角形的特殊形式.
议一议
【2】两个直角三角形一定相似吗?两个等腰直角三角形呢?为什么?
1、所有的直角三角形不都相似,如左图中的两个直角三角形就不相似;
2、所有的等腰直角三角形都相似。因为每个等腰直角三角形中都有一个直角,
两个45°的角,且两条直角边相等,斜边等于直角边的根号2倍,所以任意两个
等腰直角三角形的对应角相等,对应边
成比例。因此所有的等腰直角
三角形都相似.
议一议
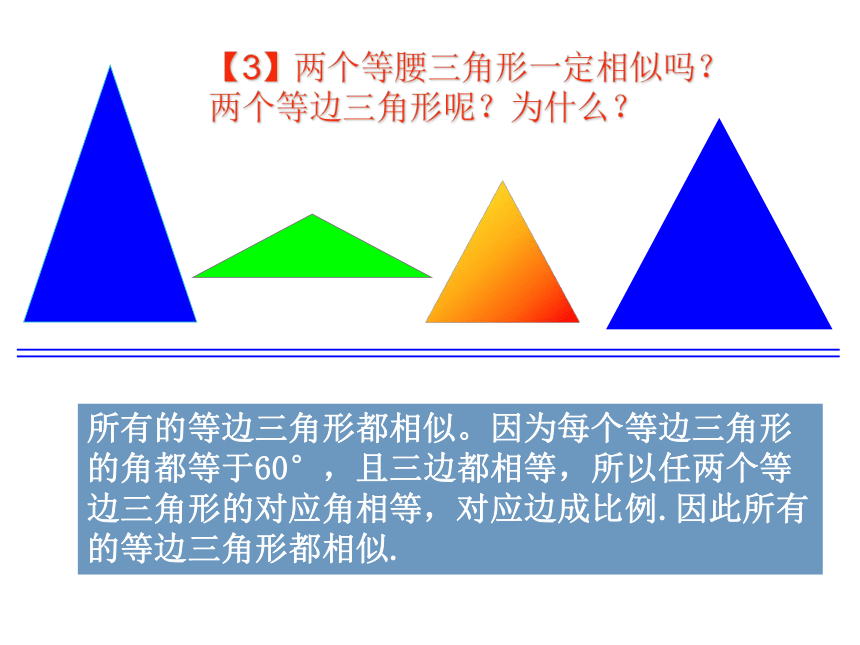
【3】两个等腰三角形一定相似吗?两个等边三角形呢?为什么?
所有的等边三角形都相似。因为每个等边三角形的角都等于60°,且三边都相等,所以任两个等边三角形的对应角相等,对应边成比例.因此所有的等边三角形都相似.
【1】两个全等三角形一定相似
【2】两个等腰直角三角形一定相似
【3】两个等边三角形一定相似
【4】两个直角三角形和两个等腰
三角形不一定相似
例题讲解
A
B
C
E
F
例:△AEF∽△ABC,
(1)若AE=3,AB=5,EF=2.4,求BC的长.
(2)求证:EF∥BC.
解:(1)∵
△AEF∽△ABC
又∵
AE=3,AB=5,EF=2.4,
∴
(2)∵
△AEF∽△ABC,
∴
∠AEF=∠B.
∴
EF∥BC.
平行于三角形一边,并且和其他两边相交的直线,所截得的三角形与原三角形对应边成比例.
A
B
C
D
E
A
B
C
E
D
截得的三角形与原三角形相似
已知:如图,
EF//BC
,
与AB、AC(它们的延长线)相交于点E、F.
平行于三角形一边的直线和其他两边(或它们的延长线)相交,所截得的三角形与原三角形相似.
F
B
A
C
E
∵∠A=∠A
△AEF∽△ABC
证明:如图,在△AEF和△ABC中
∵EF∥BC
∴∠AEF=∠B,∠AFE=∠C,
且
∴
△AEF∽△ABC
二、请同学们细心判一判
1、如果两个三角形全等,则它们必相似.
√
2、若两个三角形相似,且相似比为1,则它们必全等.
√
3、如果两个三角形与第三个三角形相似,则这两个三角形必相似.
√
4、相似的两个三角形一定大小不等.
×
试一试身手
一、填
一填
:
1、如果两个三角形的相似比为1,那么这两个三角形_____
2、若△ABC与△A′B′C′相似,一组对应边的长为AB=3
cm,A′B′=4
cm,那么△A′B′C′与△ABC的相似比是____
3、若△ABC的三条边长的比为3cm、5cm、6cm,与其相似的另一个△A′B′C′的最小边长为12
cm,那么A′B′C′的最大边长是_____
4、已知△ABC的三条边长3cm,4cm,5cm,△ABC∽△A1B1C1,那么△A1B1C1的形状是______,又知△A1B1C1的最大边长为25cm,那么△A1B1C1的面积为
全等
4︰3
24cm
直角三角形
150cm2
二、认真选一选
1、下列命题错误的是(
)
A.两个全等的三角形一定相似
B.两个直角三角形一定相似
C.两个相似三角形的对应角相等,对应边成比例
D.相似的两个三角形不一定全等
2、若△ABC∽△DEF,它们的周长分别为6
cm和8
cm,那么下式中一定成立的是(
)
A.
3AB=4DE
B.
4AC=3DE
C.
3∠A=4∠D
D.
4(AB+BC+AC)=
3(DE+EF+DF)
3、若△ABC与△A′B′C′相似,∠A=55°,∠B=100°,那么∠C’的度数是(
)
A.55°
B.100°
C.250
D.不能确定
4、把△ABC的各边分别扩大为原来的3倍,得到△A′B′C′,下列结论不能成立的是(
)
A.△ABC∽△A′B′C′
B.△ABC与△A′B′C′的各对应角相等
C.△ABC与△A′B′C′的相似比为
D.△ABC与△A′B′C′的相似比为
B
D
C
C
练习2:如图,已知△ABC∽ADE,AE=50cm,EC=30cm,BC=70cm,∠BAC=450,∠ACB=400,求⑴∠ADE和∠AED的度数;⑵DE的长
A
B
C
D
E
练习
50cm
30cm
70cm
450
400
?
解:⑴因为△ABC∽ADE,
所以由相似三角形对应角相等,
得∠AED=∠ACB=400
而在△ADE中
∠AED+∠ADE+∠A=1800,
所以∠ADE=1800-400-450=950
⑵因为△ABC∽△ADE,
所以由相似三角形
对应边成比例,
得AE∶AC=DE∶BC,
即50∶(50+30)=DE∶70,
所以DE=43.75cm
A
B
C
D
E
想一想:在上述的条件下,图中有哪些线段成比例?
线段DE与BC平行吗?为什么?
我们学了些什么?
相似三角形
定义
对应角相等
对应边成比例
表示法:
∽
相似比:
对应边的比
课外作业
见课本第63页练习第1,2题.
谢谢各位
再见
25.3.1
相似三角形
蓦然回首
1、什么叫做全等三角形?
能够完全重合的两个三角形叫做全等三角形.
(如右图△ABC≌DEF)
2、全等三角形的对应边、对应角之间各有什么关系?
性质:对应边相等、对应角相等.
A
B
C
D
E
F
1
探究新知
定义:对应角相等、对应边成比例的两个三角形叫做相似三角形.
A
B
C
E
D
F
表示:∽,相似于”
如右图:
△ABC相似于△DEF
就可表示为△ABC∽△DEF
对应顶点字母一定要写在对应位置,这样可以准确地找出相似三角形的对应角和对应边.
可要注意呀!
相似相似三角形对应边的比叫做相似比或相似系数(求相似三角形的相似比要注意顺序性)
这两个三角形的相似比怎样表示呀?
想一想
对应角相等、对应边成比例
相似三角形具有传递性
A
B
C
D
E
1、如图所示如果△ADE∽△ABC,那么哪些角是对应角?哪些边是对应边?对应角有什么关系?对应边呢?
2、如果△ABC∽△A1B1C1,
△A1B1C1∽△A2B2C2,那么△ABC与△A2B2C2相似吗?为什么?由此可得相似三角形有什么性质?
【1】两个全等三角形一定相似吗?为什么?它与相似三角形有什么关系?
两个全等三角形的对应边相等,对应角相等,由对应边相等可知对应边一定成比例,且相似比为1,因此满足相似三角形的两个条件,所以两个全等三角形一定相似.全等三角形是相似三角形的特殊形式.
议一议
【2】两个直角三角形一定相似吗?两个等腰直角三角形呢?为什么?
1、所有的直角三角形不都相似,如左图中的两个直角三角形就不相似;
2、所有的等腰直角三角形都相似。因为每个等腰直角三角形中都有一个直角,
两个45°的角,且两条直角边相等,斜边等于直角边的根号2倍,所以任意两个
等腰直角三角形的对应角相等,对应边
成比例。因此所有的等腰直角
三角形都相似.
议一议
【3】两个等腰三角形一定相似吗?两个等边三角形呢?为什么?
所有的等边三角形都相似。因为每个等边三角形的角都等于60°,且三边都相等,所以任两个等边三角形的对应角相等,对应边成比例.因此所有的等边三角形都相似.
【1】两个全等三角形一定相似
【2】两个等腰直角三角形一定相似
【3】两个等边三角形一定相似
【4】两个直角三角形和两个等腰
三角形不一定相似
例题讲解
A
B
C
E
F
例:△AEF∽△ABC,
(1)若AE=3,AB=5,EF=2.4,求BC的长.
(2)求证:EF∥BC.
解:(1)∵
△AEF∽△ABC
又∵
AE=3,AB=5,EF=2.4,
∴
(2)∵
△AEF∽△ABC,
∴
∠AEF=∠B.
∴
EF∥BC.
平行于三角形一边,并且和其他两边相交的直线,所截得的三角形与原三角形对应边成比例.
A
B
C
D
E
A
B
C
E
D
截得的三角形与原三角形相似
已知:如图,
EF//BC
,
与AB、AC(它们的延长线)相交于点E、F.
平行于三角形一边的直线和其他两边(或它们的延长线)相交,所截得的三角形与原三角形相似.
F
B
A
C
E
∵∠A=∠A
△AEF∽△ABC
证明:如图,在△AEF和△ABC中
∵EF∥BC
∴∠AEF=∠B,∠AFE=∠C,
且
∴
△AEF∽△ABC
二、请同学们细心判一判
1、如果两个三角形全等,则它们必相似.
√
2、若两个三角形相似,且相似比为1,则它们必全等.
√
3、如果两个三角形与第三个三角形相似,则这两个三角形必相似.
√
4、相似的两个三角形一定大小不等.
×
试一试身手
一、填
一填
:
1、如果两个三角形的相似比为1,那么这两个三角形_____
2、若△ABC与△A′B′C′相似,一组对应边的长为AB=3
cm,A′B′=4
cm,那么△A′B′C′与△ABC的相似比是____
3、若△ABC的三条边长的比为3cm、5cm、6cm,与其相似的另一个△A′B′C′的最小边长为12
cm,那么A′B′C′的最大边长是_____
4、已知△ABC的三条边长3cm,4cm,5cm,△ABC∽△A1B1C1,那么△A1B1C1的形状是______,又知△A1B1C1的最大边长为25cm,那么△A1B1C1的面积为
全等
4︰3
24cm
直角三角形
150cm2
二、认真选一选
1、下列命题错误的是(
)
A.两个全等的三角形一定相似
B.两个直角三角形一定相似
C.两个相似三角形的对应角相等,对应边成比例
D.相似的两个三角形不一定全等
2、若△ABC∽△DEF,它们的周长分别为6
cm和8
cm,那么下式中一定成立的是(
)
A.
3AB=4DE
B.
4AC=3DE
C.
3∠A=4∠D
D.
4(AB+BC+AC)=
3(DE+EF+DF)
3、若△ABC与△A′B′C′相似,∠A=55°,∠B=100°,那么∠C’的度数是(
)
A.55°
B.100°
C.250
D.不能确定
4、把△ABC的各边分别扩大为原来的3倍,得到△A′B′C′,下列结论不能成立的是(
)
A.△ABC∽△A′B′C′
B.△ABC与△A′B′C′的各对应角相等
C.△ABC与△A′B′C′的相似比为
D.△ABC与△A′B′C′的相似比为
B
D
C
C
练习2:如图,已知△ABC∽ADE,AE=50cm,EC=30cm,BC=70cm,∠BAC=450,∠ACB=400,求⑴∠ADE和∠AED的度数;⑵DE的长
A
B
C
D
E
练习
50cm
30cm
70cm
450
400
?
解:⑴因为△ABC∽ADE,
所以由相似三角形对应角相等,
得∠AED=∠ACB=400
而在△ADE中
∠AED+∠ADE+∠A=1800,
所以∠ADE=1800-400-450=950
⑵因为△ABC∽△ADE,
所以由相似三角形
对应边成比例,
得AE∶AC=DE∶BC,
即50∶(50+30)=DE∶70,
所以DE=43.75cm
A
B
C
D
E
想一想:在上述的条件下,图中有哪些线段成比例?
线段DE与BC平行吗?为什么?
我们学了些什么?
相似三角形
定义
对应角相等
对应边成比例
表示法:
∽
相似比:
对应边的比
课外作业
见课本第63页练习第1,2题.
谢谢各位
再见
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
