冀教版数学九年级上册 25.4 相似三角形的判定 课件(第2课时 共18张PPT)
文档属性
| 名称 | 冀教版数学九年级上册 25.4 相似三角形的判定 课件(第2课时 共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 233.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-13 14:40:00 | ||
图片预览



文档简介
(共18张PPT)
25.4.2相似三角形的判定(2)
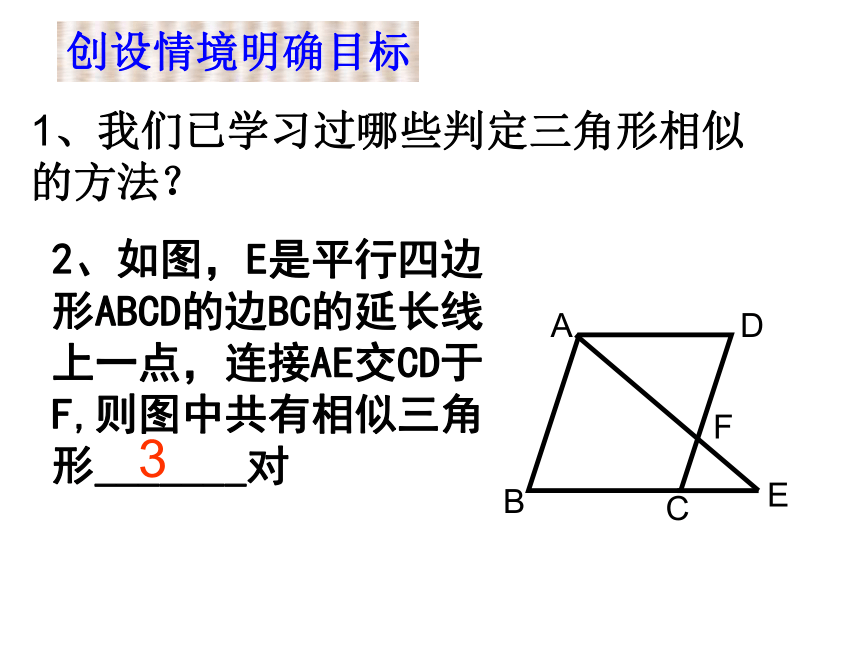
A
B
C
D
E
F
2、如图,E是平行四边形ABCD的边BC的延长线上一点,连接AE交CD于F,则图中共有相似三角形_______对
3
创设情境明确目标
1、我们已学习过哪些判定三角形相似的方法?
A
B
D
C
图
1
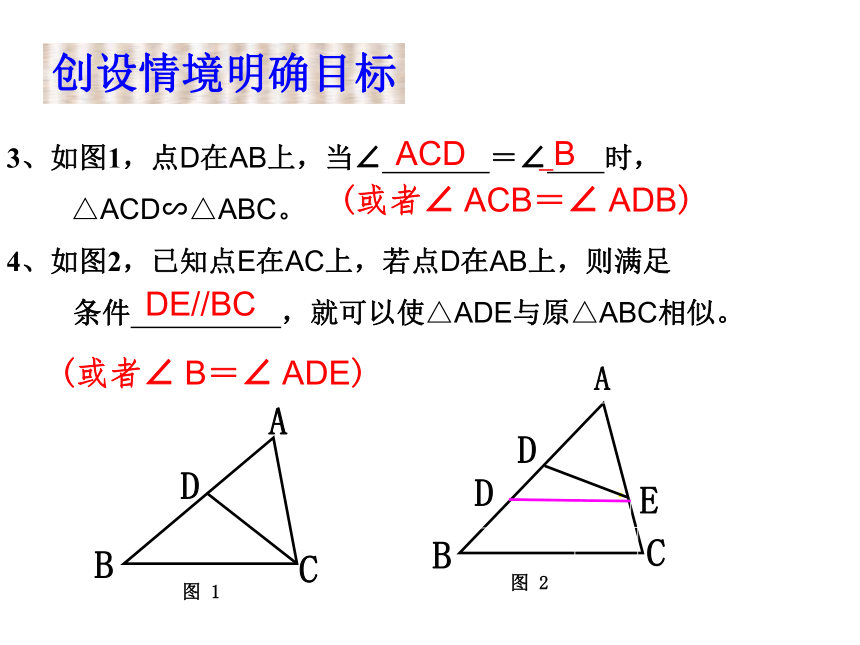
3、如图1,点D在AB上,当∠
=∠
时,
△ACD∽△ABC。
4、如图2,已知点E在AC上,若点D在AB上,则满足
条件
,就可以使△ADE与原△ABC相似。
●
A
B
C
E
图
2
ACD
B
(或者∠
ACB=∠
ADB)
DE//BC
D
(或者∠
B=∠
ADE)
D
创设情境明确目标
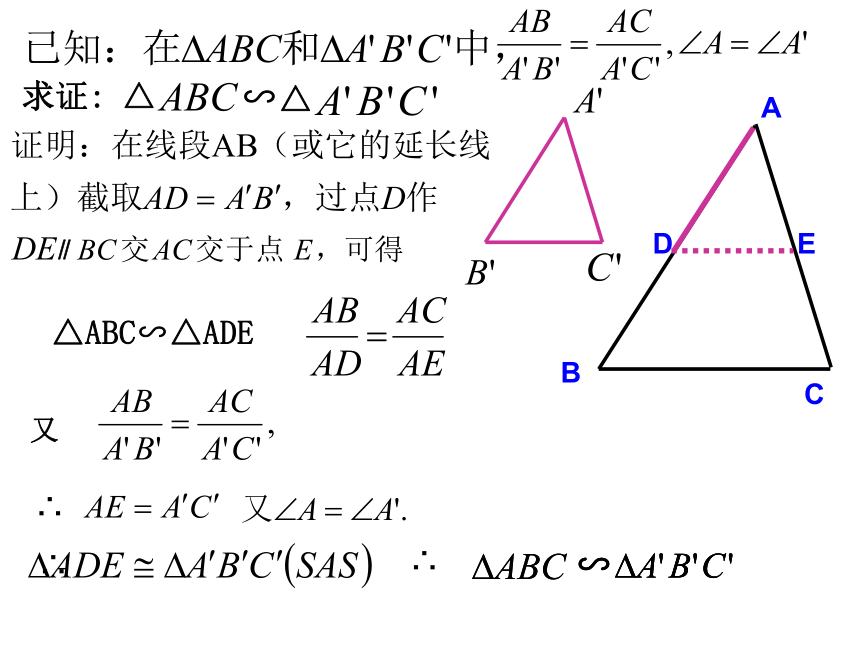
类似于判定三角形全等的SAS方法,我们能不能通过两边及其夹角来判定两个三角形相似呢?
三角形的判定全等有SSS、SAS
ASA、AAS
猜想
改变k和∠A的值的大小,是否有同样的结论?
探究
求证:
△
∽△
A
B
C
D
E
又
∴
∴
∥
∽
∴
∽
∽
△ABC∽△ADE
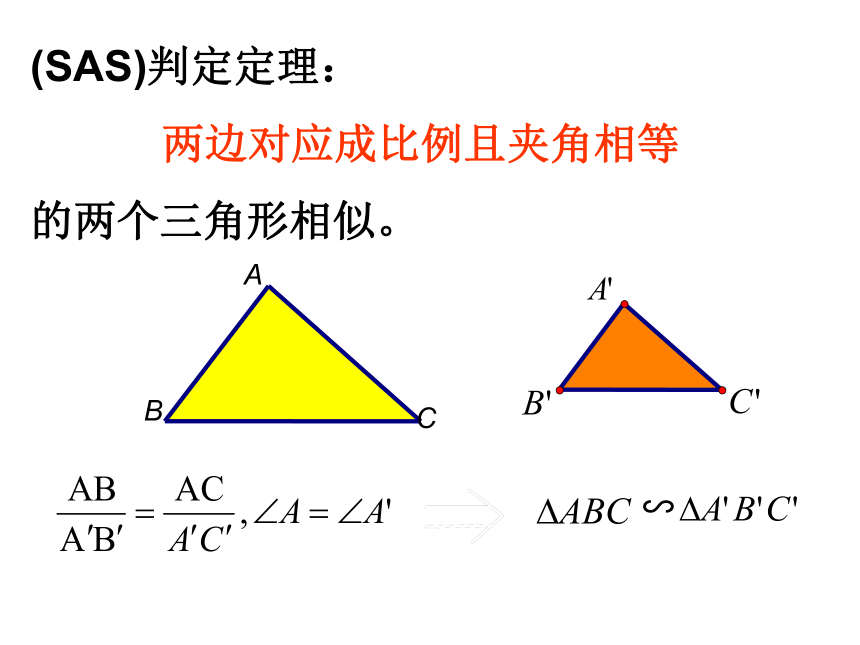
(SAS)判定定理:
两边对应成比例且夹角相等
的两个三角形相似。
A
B
C
∽
猜想:
对于△ABC和△A`B`C`
如果
AB:A`B`=
AC:A`C`.
∠B=
∠B`,这两个三角形一定会相似吗?
不会,因为不能证明构造的三角形和原三角形全等
A
B
C
解
∵
AB/A’B’=7/3
AC/A’C’=14/6=7/3
∴
AB/A’B’=
AC/A’C’
又
∠A=
∠A’=60°
∴
△ABC∽△A`B`C`
AB=7,
AC=14,
∠A=60°
A’B’=3,A’C’=6,
∠A’=
60°
AB=7,
AC=14,
∠A=60°
A’B’=6,A’C’=3,
∠A’=
60°
例2:根据下列条件,判断△ABC和△A’B’C’
是否相似,并说明理由。
变式
理解
练习:
1.
2.图中两个三角形是否相似?
6
3
10
5
C
A
B
E
E
不相似
相似
2、如图,AB?AE=AD?AC,且∠1=∠2,
求证:△ABC∽△AED.
3.已知:如图,P为△ABC中线AD上
的一点,且
求证:△ADC∽△CDP.
方法2:
平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似;
方法3:两角对应相等,两三角形相似。
相似三角形的判定方法
方法4:两边对应成比例且夹角相等,两三角形相似.
方法1:通过定义(不常用)
小结
达标测评
1.如图,△ABC中,DE∥BC,F是AB上的点,AD?=AB·AF,请问:EF是否与CD平行?说明理由.
2.已知:如图,D、E分别是AB、AC上两点,CD、BE交于O,如果AD·AB=AE·AC,请问△ODB与△OEC相似吗?为什么?
达标测评
3.(2014?碑林区一模)下列五幅图均是由边长为1的16个小正方形组成的正方形网格,网格中的三角形的顶点都在小正方形的顶点上,那么在下列右边四幅图中的三角形,与左图中的△ABC相似的个数有( )
A.1个
B.2个
C.3个
D.4个
达标测评
B
见课本第70页第1,2,3题.
课后作业
如图,AB⊥BC,DC⊥BC,垂足分别为B、C,且AB=8,DC=6,BC=14,BC上是否存在点P使△ABP与△DCP相似?若有,有几个?并求出此时BP的长,若没有,请说明理由.
8
6
14
思考
25.4.2相似三角形的判定(2)
A
B
C
D
E
F
2、如图,E是平行四边形ABCD的边BC的延长线上一点,连接AE交CD于F,则图中共有相似三角形_______对
3
创设情境明确目标
1、我们已学习过哪些判定三角形相似的方法?
A
B
D
C
图
1
3、如图1,点D在AB上,当∠
=∠
时,
△ACD∽△ABC。
4、如图2,已知点E在AC上,若点D在AB上,则满足
条件
,就可以使△ADE与原△ABC相似。
●
A
B
C
E
图
2
ACD
B
(或者∠
ACB=∠
ADB)
DE//BC
D
(或者∠
B=∠
ADE)
D
创设情境明确目标
类似于判定三角形全等的SAS方法,我们能不能通过两边及其夹角来判定两个三角形相似呢?
三角形的判定全等有SSS、SAS
ASA、AAS
猜想
改变k和∠A的值的大小,是否有同样的结论?
探究
求证:
△
∽△
A
B
C
D
E
又
∴
∴
∥
∽
∴
∽
∽
△ABC∽△ADE
(SAS)判定定理:
两边对应成比例且夹角相等
的两个三角形相似。
A
B
C
∽
猜想:
对于△ABC和△A`B`C`
如果
AB:A`B`=
AC:A`C`.
∠B=
∠B`,这两个三角形一定会相似吗?
不会,因为不能证明构造的三角形和原三角形全等
A
B
C
解
∵
AB/A’B’=7/3
AC/A’C’=14/6=7/3
∴
AB/A’B’=
AC/A’C’
又
∠A=
∠A’=60°
∴
△ABC∽△A`B`C`
AB=7,
AC=14,
∠A=60°
A’B’=3,A’C’=6,
∠A’=
60°
AB=7,
AC=14,
∠A=60°
A’B’=6,A’C’=3,
∠A’=
60°
例2:根据下列条件,判断△ABC和△A’B’C’
是否相似,并说明理由。
变式
理解
练习:
1.
2.图中两个三角形是否相似?
6
3
10
5
C
A
B
E
E
不相似
相似
2、如图,AB?AE=AD?AC,且∠1=∠2,
求证:△ABC∽△AED.
3.已知:如图,P为△ABC中线AD上
的一点,且
求证:△ADC∽△CDP.
方法2:
平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似;
方法3:两角对应相等,两三角形相似。
相似三角形的判定方法
方法4:两边对应成比例且夹角相等,两三角形相似.
方法1:通过定义(不常用)
小结
达标测评
1.如图,△ABC中,DE∥BC,F是AB上的点,AD?=AB·AF,请问:EF是否与CD平行?说明理由.
2.已知:如图,D、E分别是AB、AC上两点,CD、BE交于O,如果AD·AB=AE·AC,请问△ODB与△OEC相似吗?为什么?
达标测评
3.(2014?碑林区一模)下列五幅图均是由边长为1的16个小正方形组成的正方形网格,网格中的三角形的顶点都在小正方形的顶点上,那么在下列右边四幅图中的三角形,与左图中的△ABC相似的个数有( )
A.1个
B.2个
C.3个
D.4个
达标测评
B
见课本第70页第1,2,3题.
课后作业
如图,AB⊥BC,DC⊥BC,垂足分别为B、C,且AB=8,DC=6,BC=14,BC上是否存在点P使△ABP与△DCP相似?若有,有几个?并求出此时BP的长,若没有,请说明理由.
8
6
14
思考
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
