人教版数学七年级上册 1.3.1 有理数的加法课件(共20张PPT)
文档属性
| 名称 | 人教版数学七年级上册 1.3.1 有理数的加法课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 944.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-13 00:00:00 | ||
图片预览


文档简介
(共20张PPT)
有理数的加法
初中数学
七年级
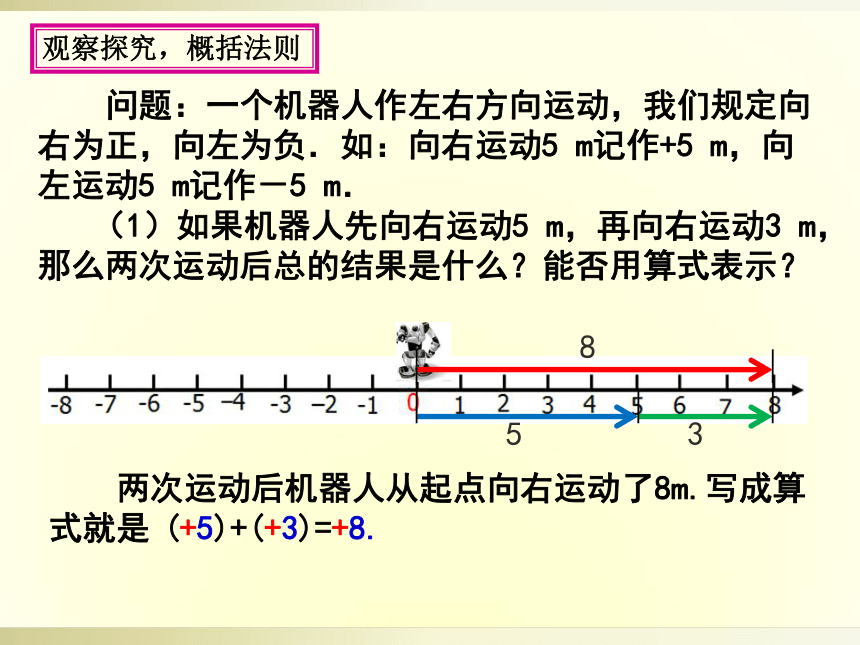
问题:一个机器人作左右方向运动,我们规定向右为正,向左为负.如:向右运动5
m记作+5
m,向左运动5
m记作-5
m.
(1)如果机器人先向右运动5
m,再向右运动3
m,那么两次运动后总的结果是什么?能否用算式表示?
5
3
8
两次运动后机器人从起点向右运动了8m.写成算式就是
(+5)+(+3)=+8.
观察探究,概括法则
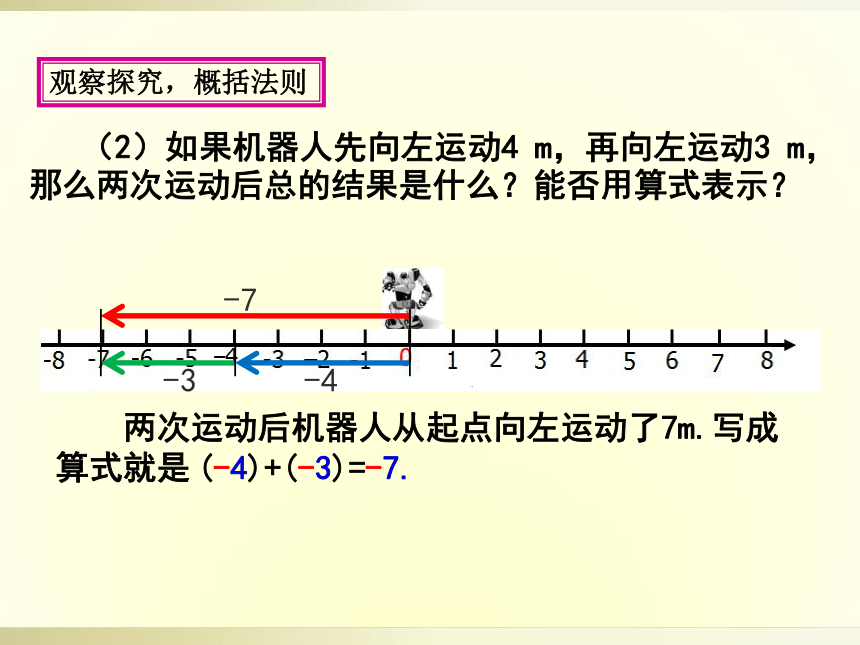
(-4)+(-3)=-7.
(2)如果机器人先向左运动4
m,再向左运动3
m,那么两次运动后总的结果是什么?能否用算式表示?
-4
-3
-7
两次运动后机器人从起点向左运动了7m.写成算式就是
观察探究,概括法则
(+5)+(+3)=
(-4)+(-3)=
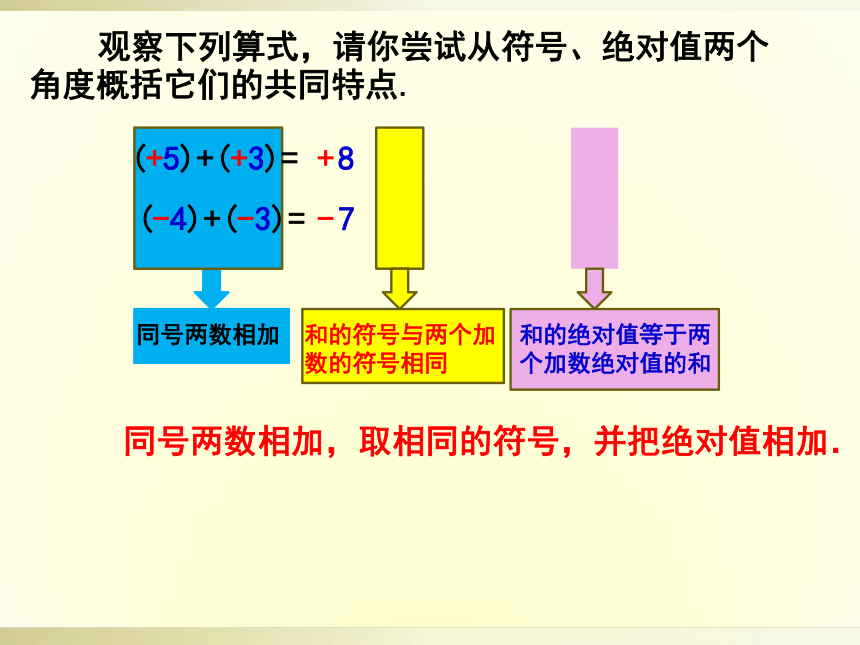
观察下列算式,请你尝试从符号、绝对值两个角度概括它们的共同特点.
同号两数相加,取相同的符号,并把绝对值相加.
同号两数相加
和的符号与两个加数的符号相同
和的绝对值等于两个加数绝对值的和
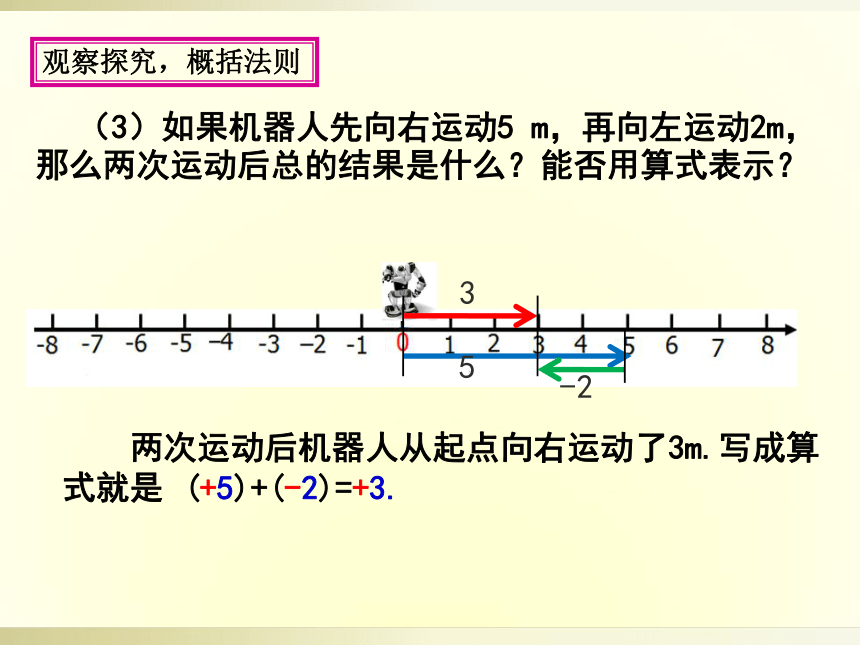
(+5)+(-2)=+3.
(3)如果机器人先向右运动5
m,再向左运动2m,那么两次运动后总的结果是什么?能否用算式表示?
5
-2
3
两次运动后机器人从起点向右运动了3m.写成算式就是
观察探究,概括法则
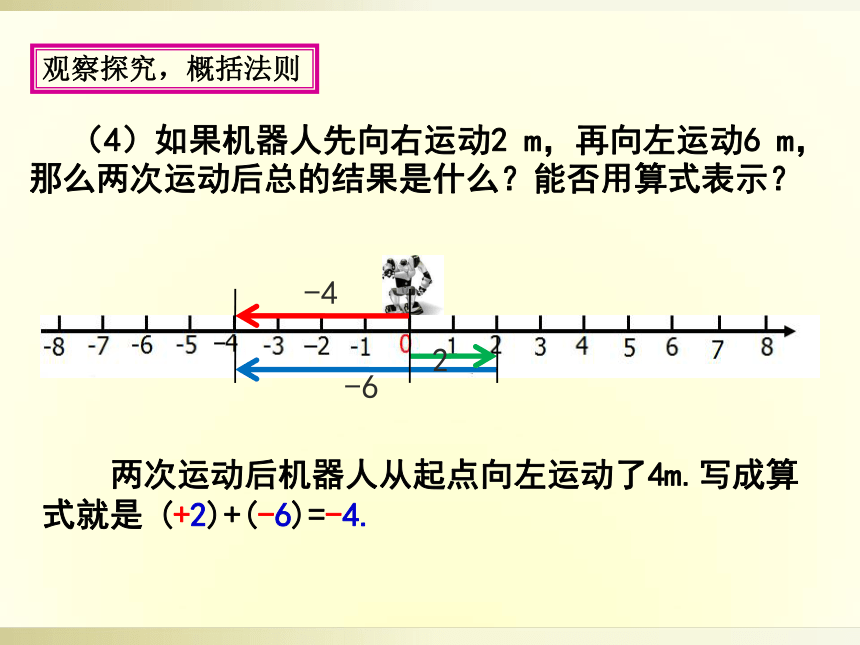
(+2)+(-6)=-4.
(4)如果机器人先向右运动2
m,再向左运动6
m,那么两次运动后总的结果是什么?能否用算式表示?
-6
2
-4
两次运动后机器人从起点向左运动了4m.写成算式就是
观察探究,概括法则
(+5)+(-2)=
(+2)+(-6)=
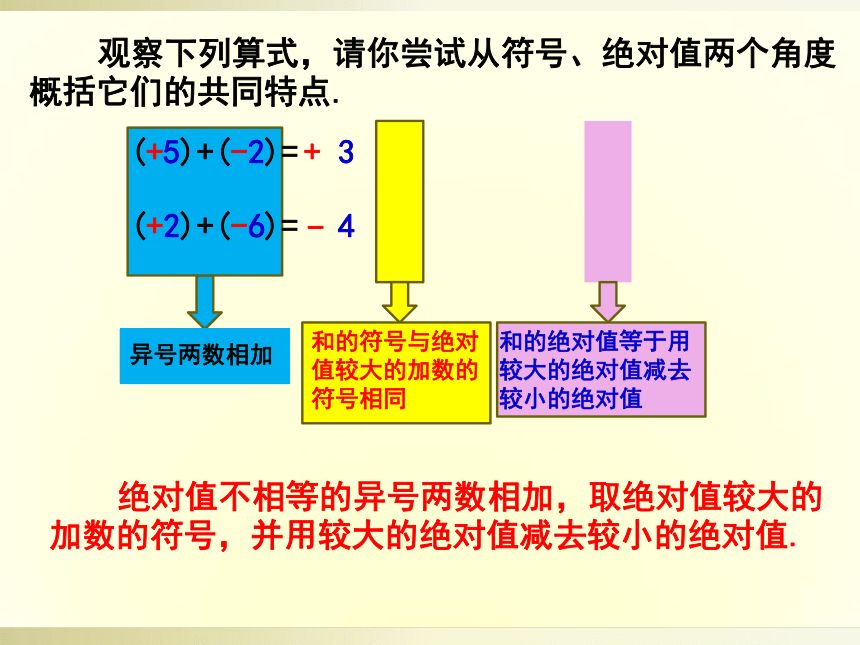
观察下列算式,请你尝试从符号、绝对值两个角度概括它们的共同特点.
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
异号两数相加
和的符号与绝对值较大的加数的符号相同
和的绝对值等于用较大的绝对值减去较小的绝对值
(+5)+(-5
)=0.
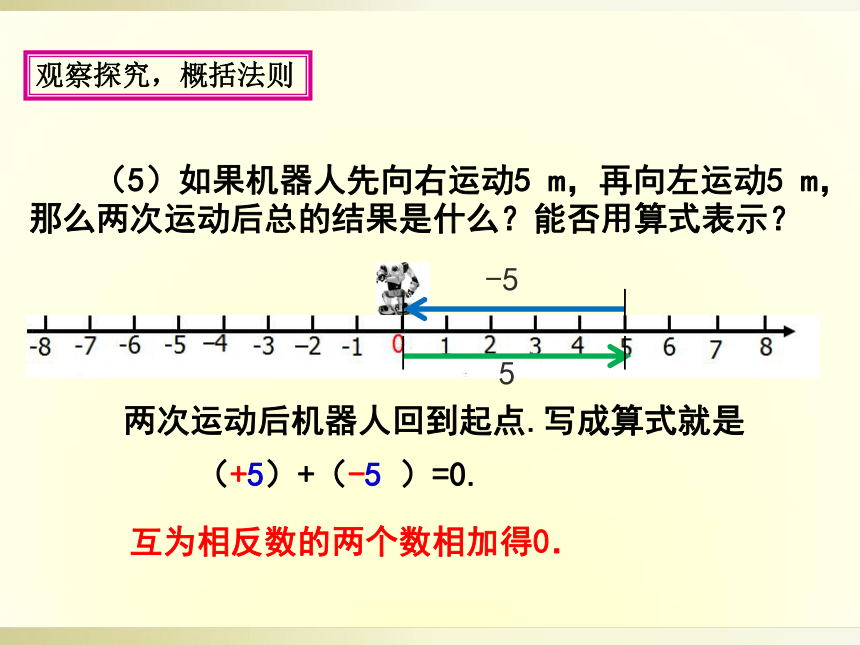
(5)如果机器人先向右运动5
m,再向左运动5
m,那么两次运动后总的结果是什么?能否用算式表示?
-5
5
互为相反数的两个数相加得0.
两次运动后机器人回到起点.写成算式就是
观察探究,概括法则
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.
观察探究,概括法则
写成算式就是(-5)+0=-5
(或5+0=5).
(6)如果机器人第1秒向左(或右)运动5
m,第2秒原地不动,很显然,两秒后机器人从起点向左(或右)运动5
m.如何用算式表示呢?
一个数同0相加,仍得这个数.
观察探究,概括法则
归纳有理数加法法则:
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
观察探究,概括法则
例1.计算:(1)(-3)+(-9);
解:(1)(-3)+(-9)=
同号两数相加
取相同的符号
把绝对值相加
=-12
(3+9)
-
举例示范,巩固法则
例1.计算:(2)
(-4.7)
+3.9
;
(2)
(-4.7)
+3.9
=
异号两数相加
=-0.8
(4.7-3.9)
-
取绝对值较大的加数的符号
用较大的绝对值减去较小的绝对值
举例示范,巩固法则
例1.计算:(3)
0+(-7);
(3)
0+(-7)
=-7
一个数同0相加
仍得这个数
举例示范,巩固法则
例1.计算:(4)(-9)+(+9);
(4)(-9)+(+9)
=0
互为相反数的两数相加
和为0
举例示范,巩固法则
例2.用算式表示下面的结果:
(1)温度由-9
°C上升6°C;
(2)收入7元,又支出5元.
解:(1)(-9)+
6
(2)(+7)+(-5)
=-3(°C);
=2(元).
举例示范,巩固法则
同号两数相加
异号两数相加
一个数同
0
相加
取相同的符号
把绝对值相加
绝对值不相等的
异号两数相加
互为相反数的
两个数相加
取绝对值较大
的加数的符号
用较大的绝对值减
去较小的绝对值
仍得这个数
得0
课堂小结
1.已知有理数a、b、c在数轴上的位置如图所示,则a+b__
0;
a+c___0
(用
>、<、=
填空)
.
>
<
拓展、提高
分析:根据a、b在数轴上的位置可知
a<0,
b>0,且
?b?>?a?.
所以a+b>0.
分析:根据a、c在数轴上的位置可知
a<0,
c<0.
所以a+c<0.
2.若?x?=3,
?y?=2,且x解:因为?x?
=3,?y?
?2,
所以
x?3或
?
3,
y?2或?2,
因为x所以
x??3,
y?2或?2,
所以x?y?
(?3)?2??1或
(?3)?(?2)??5.
拓展、提高
再见!
有理数的加法
初中数学
七年级
问题:一个机器人作左右方向运动,我们规定向右为正,向左为负.如:向右运动5
m记作+5
m,向左运动5
m记作-5
m.
(1)如果机器人先向右运动5
m,再向右运动3
m,那么两次运动后总的结果是什么?能否用算式表示?
5
3
8
两次运动后机器人从起点向右运动了8m.写成算式就是
(+5)+(+3)=+8.
观察探究,概括法则
(-4)+(-3)=-7.
(2)如果机器人先向左运动4
m,再向左运动3
m,那么两次运动后总的结果是什么?能否用算式表示?
-4
-3
-7
两次运动后机器人从起点向左运动了7m.写成算式就是
观察探究,概括法则
(+5)+(+3)=
(-4)+(-3)=
观察下列算式,请你尝试从符号、绝对值两个角度概括它们的共同特点.
同号两数相加,取相同的符号,并把绝对值相加.
同号两数相加
和的符号与两个加数的符号相同
和的绝对值等于两个加数绝对值的和
(+5)+(-2)=+3.
(3)如果机器人先向右运动5
m,再向左运动2m,那么两次运动后总的结果是什么?能否用算式表示?
5
-2
3
两次运动后机器人从起点向右运动了3m.写成算式就是
观察探究,概括法则
(+2)+(-6)=-4.
(4)如果机器人先向右运动2
m,再向左运动6
m,那么两次运动后总的结果是什么?能否用算式表示?
-6
2
-4
两次运动后机器人从起点向左运动了4m.写成算式就是
观察探究,概括法则
(+5)+(-2)=
(+2)+(-6)=
观察下列算式,请你尝试从符号、绝对值两个角度概括它们的共同特点.
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
异号两数相加
和的符号与绝对值较大的加数的符号相同
和的绝对值等于用较大的绝对值减去较小的绝对值
(+5)+(-5
)=0.
(5)如果机器人先向右运动5
m,再向左运动5
m,那么两次运动后总的结果是什么?能否用算式表示?
-5
5
互为相反数的两个数相加得0.
两次运动后机器人回到起点.写成算式就是
观察探究,概括法则
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.
观察探究,概括法则
写成算式就是(-5)+0=-5
(或5+0=5).
(6)如果机器人第1秒向左(或右)运动5
m,第2秒原地不动,很显然,两秒后机器人从起点向左(或右)运动5
m.如何用算式表示呢?
一个数同0相加,仍得这个数.
观察探究,概括法则
归纳有理数加法法则:
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
观察探究,概括法则
例1.计算:(1)(-3)+(-9);
解:(1)(-3)+(-9)=
同号两数相加
取相同的符号
把绝对值相加
=-12
(3+9)
-
举例示范,巩固法则
例1.计算:(2)
(-4.7)
+3.9
;
(2)
(-4.7)
+3.9
=
异号两数相加
=-0.8
(4.7-3.9)
-
取绝对值较大的加数的符号
用较大的绝对值减去较小的绝对值
举例示范,巩固法则
例1.计算:(3)
0+(-7);
(3)
0+(-7)
=-7
一个数同0相加
仍得这个数
举例示范,巩固法则
例1.计算:(4)(-9)+(+9);
(4)(-9)+(+9)
=0
互为相反数的两数相加
和为0
举例示范,巩固法则
例2.用算式表示下面的结果:
(1)温度由-9
°C上升6°C;
(2)收入7元,又支出5元.
解:(1)(-9)+
6
(2)(+7)+(-5)
=-3(°C);
=2(元).
举例示范,巩固法则
同号两数相加
异号两数相加
一个数同
0
相加
取相同的符号
把绝对值相加
绝对值不相等的
异号两数相加
互为相反数的
两个数相加
取绝对值较大
的加数的符号
用较大的绝对值减
去较小的绝对值
仍得这个数
得0
课堂小结
1.已知有理数a、b、c在数轴上的位置如图所示,则a+b__
0;
a+c___0
(用
>、<、=
填空)
.
>
<
拓展、提高
分析:根据a、b在数轴上的位置可知
a<0,
b>0,且
?b?>?a?.
所以a+b>0.
分析:根据a、c在数轴上的位置可知
a<0,
c<0.
所以a+c<0.
2.若?x?=3,
?y?=2,且x
=3,?y?
?2,
所以
x?3或
?
3,
y?2或?2,
因为x
x??3,
y?2或?2,
所以x?y?
(?3)?2??1或
(?3)?(?2)??5.
拓展、提高
再见!
