第一章 三角形章末复习题(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第一章 三角形
章末复习
考点突破
考点1 三角形的有关概念及内角和
1.如图,图中以AB为边的三角形的个数共有( )
A.1个 B.2个 C.3个 D.4个
2.如图,在△ABC中,点D在BA的延长线上,DE∥BC.如果∠BAC=65°,∠C=30°,那么∠BDE的度数是___________。
3.将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1+∠2的度数为____________。
考点2 三角形的三边关系
4.(长沙中考)下列长度的三条线段,能组成三角形的是( )
A.4 cm,5 cm, cm B.8 cm, 8 cm, 15 cm
C. 5 cm, 5 cm, 10 cm D.6 cm,7 cm,14 cm
5.(泰州中考)已知三角形两边的长分别为1,5,第三边长为整数,则第三边的长为__________。
考点3 三角形的中线、角平分线和高线
6.已知AD为△ABC的中线,AB=5 cm,且△ACD的周长比△ABD的周长少2 cm,则AC=________。
7.如图,AE是△ABC的角平分线,AD⊥BC于点D若∠BAC=130°,∠C=30°,则∠DAE的度数是___________。
考点4 全等三角形的性质与条件
8.(淄博校级期中联考)如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△AF≌△CBE的是( )
A.∠A=∠C B.AD=CB C. BE=DF D.AD∥BC
9.如图,OA=OC,OB=OD,OA⊥OB,OC⊥OD,下列结论:①△AOD≌△COB;②CD=AB;③∠CDA=∠ABC.其中正确的结论是( )
A.①② B.①②③ C.①③ D.②③
10.(淄博中考)已知,在如图所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠E=∠C.
易错易混
等腰三角形的底边未确定导致漏解
11.如果等腰三角形两边长分别是6和4,那么它的周长是( )
A.14 B.10 C.16 D.16或14
高频集训
12.(枣庄中考)一副直角三角按如图所水的位置放置,使含30°角的三角板的一条自角边和含45°角的三角板的一条直角边放在同一条直线上,则∠a的度数是( )
A.45° B.60° C.75° D.85°
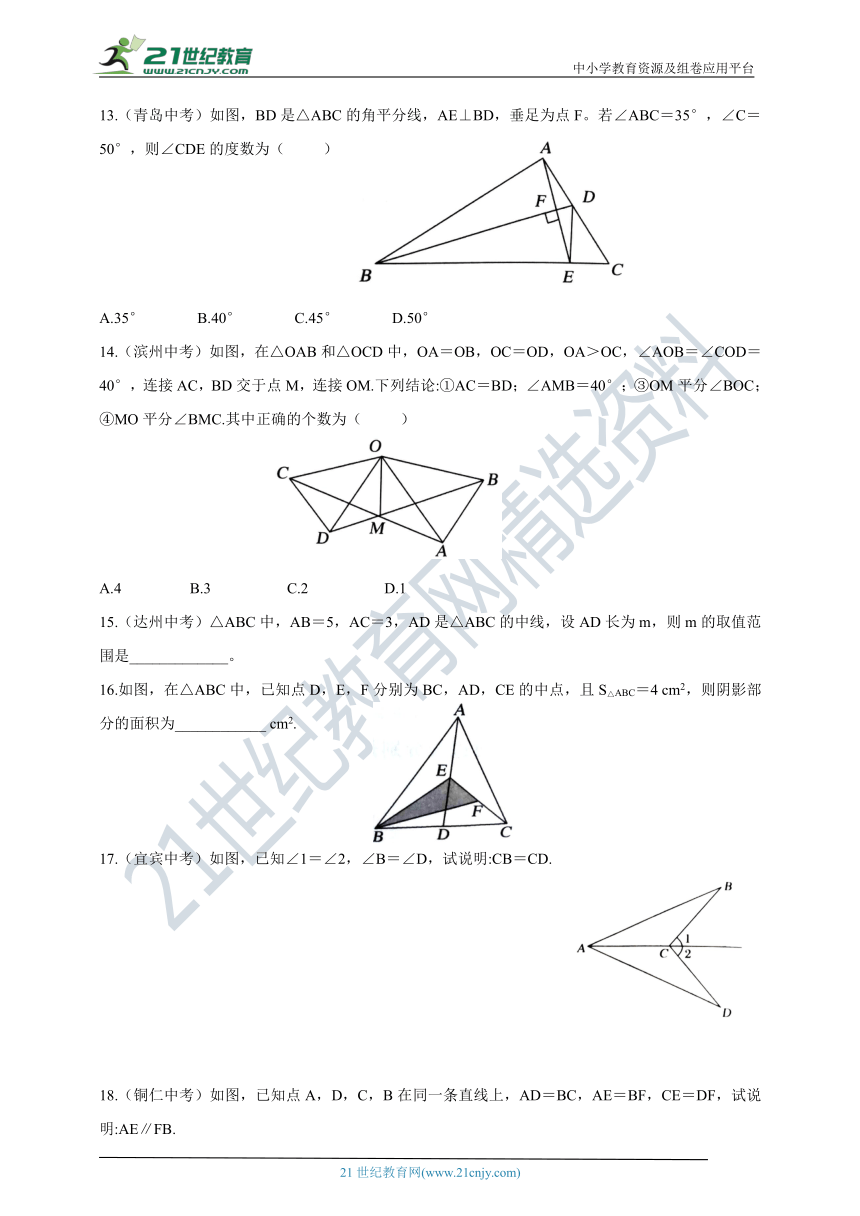
13.(青岛中考)如图,BD是△ABC的角平分线,AE⊥BD,垂足为点F。若∠ABC=35°,∠C=50°,则∠CDE的度数为( )
A.35° B.40° C.45° D.50°
14.(滨州中考)如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为( )
A.4 B.3 C.2 D.1
15.(达州中考)△ABC中,AB=5,AC=3,AD是△ABC的中线,设AD长为m,则m的取值范围是_____________。
16.如图,在△ABC中,已知点D,E,F分别为BC,AD,CE的中点,且S△ABC=4 cm2,则阴影部分的面积为____________ cm2.
17.(宜宾中考)如图,已知∠1=∠2,∠B=∠D,试说明:CB=CD.
18.(铜仁中考)如图,已知点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF,试说明:AE∥FB.
参考答案
1.B 2.95° 3.210° 4.B 5. 5 6. 3cm 7.5° 8.B 9.B
10.解:因为∠BAE=∠DAC,所以∠BAE+∠CAE=∠DAC+∠CAE,即∠CAB=∠EAD。
又因为AB=AD,AC=AE,所以△ABC≌△ADE(SAS),所以∠C=∠E.
11.D
12.C【解析】如图,
因为∠ACD=90°,∠F=45°,所以∠CGF=∠DGB=45°
因为∠DGB+∠D+∠GHD=180°,∠GHD+∠a=180°,
所以∠a=∠D+∠DGB=30°+45°=75°
故选C
13.C【解析】因为BD是△ABC的角平分线,AE⊥BD,
所以∠ABD=∠EBD=∠ABC==17.5°,∠AFB=∠EFB。
因为BF=BF,所以△ABF≌△EBF(ASA),所以AB=BE.
因为∠ABC=35°,∠C=50°,所以∠BAC=180°-∠ABC-∠C=95°,所以∠ADB=67.5°。
在△ABD与△EBD中,因为,所以△ABD≌△EBD(SAS).
所以∠ADB=∠BDE,所以∠ADE=2∠ADB=135°,所以∠CDE=180°-∠ADE=45°。
故选C.
14.B【解析】因为∠AOB=∠COD=40°,所以∠AOB+∠AOD=∠COD+∠AOD,
即∠AOC=∠BOD,
在△AOC和△BOD中,因为,所以△AOC≌△BOD(SAS).
所以∠OCA=∠ODB,AC=BD,①正确;
所以∠OAC=∠OBD.
由题意得:∠AMB+∠OAC=∠AOB+∠OBD,所以∠AMB=∠AOB=40°,②正确;
如图,作OG⊥MC于点G,OH⊥MB于点H.
则∠OGC=∠OHD=90°
在△OCG和△ODH中,因为,所以△OCG≌△ODH(AAS).
所以OG=OH.所以MO平分∠BMC,④正确;
正确的个数有3个故选B.
15.1<m<4 16.1
17.解:因为∠1=∠2,所以∠ACB=∠ACD。
在△ABC与△ADC中,因为所以△ABC≌△ADC(AAS).所以CB=CD.
18.解:因为AD=BC,所以AD+CD=BC+CD,即AC=BD。
在△ACE和△BDF中,AC=BD,AE=BF,CE=DF,所以△ACE≌△BDF(SSS).
所以∠A=∠B.所以AE∥BF。
_21?????????è?????(www.21cnjy.com)_
第一章 三角形
章末复习
考点突破
考点1 三角形的有关概念及内角和
1.如图,图中以AB为边的三角形的个数共有( )
A.1个 B.2个 C.3个 D.4个
2.如图,在△ABC中,点D在BA的延长线上,DE∥BC.如果∠BAC=65°,∠C=30°,那么∠BDE的度数是___________。
3.将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1+∠2的度数为____________。
考点2 三角形的三边关系
4.(长沙中考)下列长度的三条线段,能组成三角形的是( )
A.4 cm,5 cm, cm B.8 cm, 8 cm, 15 cm
C. 5 cm, 5 cm, 10 cm D.6 cm,7 cm,14 cm
5.(泰州中考)已知三角形两边的长分别为1,5,第三边长为整数,则第三边的长为__________。
考点3 三角形的中线、角平分线和高线
6.已知AD为△ABC的中线,AB=5 cm,且△ACD的周长比△ABD的周长少2 cm,则AC=________。
7.如图,AE是△ABC的角平分线,AD⊥BC于点D若∠BAC=130°,∠C=30°,则∠DAE的度数是___________。
考点4 全等三角形的性质与条件
8.(淄博校级期中联考)如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△AF≌△CBE的是( )
A.∠A=∠C B.AD=CB C. BE=DF D.AD∥BC
9.如图,OA=OC,OB=OD,OA⊥OB,OC⊥OD,下列结论:①△AOD≌△COB;②CD=AB;③∠CDA=∠ABC.其中正确的结论是( )
A.①② B.①②③ C.①③ D.②③
10.(淄博中考)已知,在如图所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠E=∠C.
易错易混
等腰三角形的底边未确定导致漏解
11.如果等腰三角形两边长分别是6和4,那么它的周长是( )
A.14 B.10 C.16 D.16或14
高频集训
12.(枣庄中考)一副直角三角按如图所水的位置放置,使含30°角的三角板的一条自角边和含45°角的三角板的一条直角边放在同一条直线上,则∠a的度数是( )
A.45° B.60° C.75° D.85°
13.(青岛中考)如图,BD是△ABC的角平分线,AE⊥BD,垂足为点F。若∠ABC=35°,∠C=50°,则∠CDE的度数为( )
A.35° B.40° C.45° D.50°
14.(滨州中考)如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为( )
A.4 B.3 C.2 D.1
15.(达州中考)△ABC中,AB=5,AC=3,AD是△ABC的中线,设AD长为m,则m的取值范围是_____________。
16.如图,在△ABC中,已知点D,E,F分别为BC,AD,CE的中点,且S△ABC=4 cm2,则阴影部分的面积为____________ cm2.
17.(宜宾中考)如图,已知∠1=∠2,∠B=∠D,试说明:CB=CD.
18.(铜仁中考)如图,已知点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF,试说明:AE∥FB.
参考答案
1.B 2.95° 3.210° 4.B 5. 5 6. 3cm 7.5° 8.B 9.B
10.解:因为∠BAE=∠DAC,所以∠BAE+∠CAE=∠DAC+∠CAE,即∠CAB=∠EAD。
又因为AB=AD,AC=AE,所以△ABC≌△ADE(SAS),所以∠C=∠E.
11.D
12.C【解析】如图,
因为∠ACD=90°,∠F=45°,所以∠CGF=∠DGB=45°
因为∠DGB+∠D+∠GHD=180°,∠GHD+∠a=180°,
所以∠a=∠D+∠DGB=30°+45°=75°
故选C
13.C【解析】因为BD是△ABC的角平分线,AE⊥BD,
所以∠ABD=∠EBD=∠ABC==17.5°,∠AFB=∠EFB。
因为BF=BF,所以△ABF≌△EBF(ASA),所以AB=BE.
因为∠ABC=35°,∠C=50°,所以∠BAC=180°-∠ABC-∠C=95°,所以∠ADB=67.5°。
在△ABD与△EBD中,因为,所以△ABD≌△EBD(SAS).
所以∠ADB=∠BDE,所以∠ADE=2∠ADB=135°,所以∠CDE=180°-∠ADE=45°。
故选C.
14.B【解析】因为∠AOB=∠COD=40°,所以∠AOB+∠AOD=∠COD+∠AOD,
即∠AOC=∠BOD,
在△AOC和△BOD中,因为,所以△AOC≌△BOD(SAS).
所以∠OCA=∠ODB,AC=BD,①正确;
所以∠OAC=∠OBD.
由题意得:∠AMB+∠OAC=∠AOB+∠OBD,所以∠AMB=∠AOB=40°,②正确;
如图,作OG⊥MC于点G,OH⊥MB于点H.
则∠OGC=∠OHD=90°
在△OCG和△ODH中,因为,所以△OCG≌△ODH(AAS).
所以OG=OH.所以MO平分∠BMC,④正确;
正确的个数有3个故选B.
15.1<m<4 16.1
17.解:因为∠1=∠2,所以∠ACB=∠ACD。
在△ABC与△ADC中,因为所以△ABC≌△ADC(AAS).所以CB=CD.
18.解:因为AD=BC,所以AD+CD=BC+CD,即AC=BD。
在△ACE和△BDF中,AC=BD,AE=BF,CE=DF,所以△ACE≌△BDF(SSS).
所以∠A=∠B.所以AE∥BF。
_21?????????è?????(www.21cnjy.com)_
