第一章 三角形综合训练题(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
第一章 三角形
综合训练
一、选择题
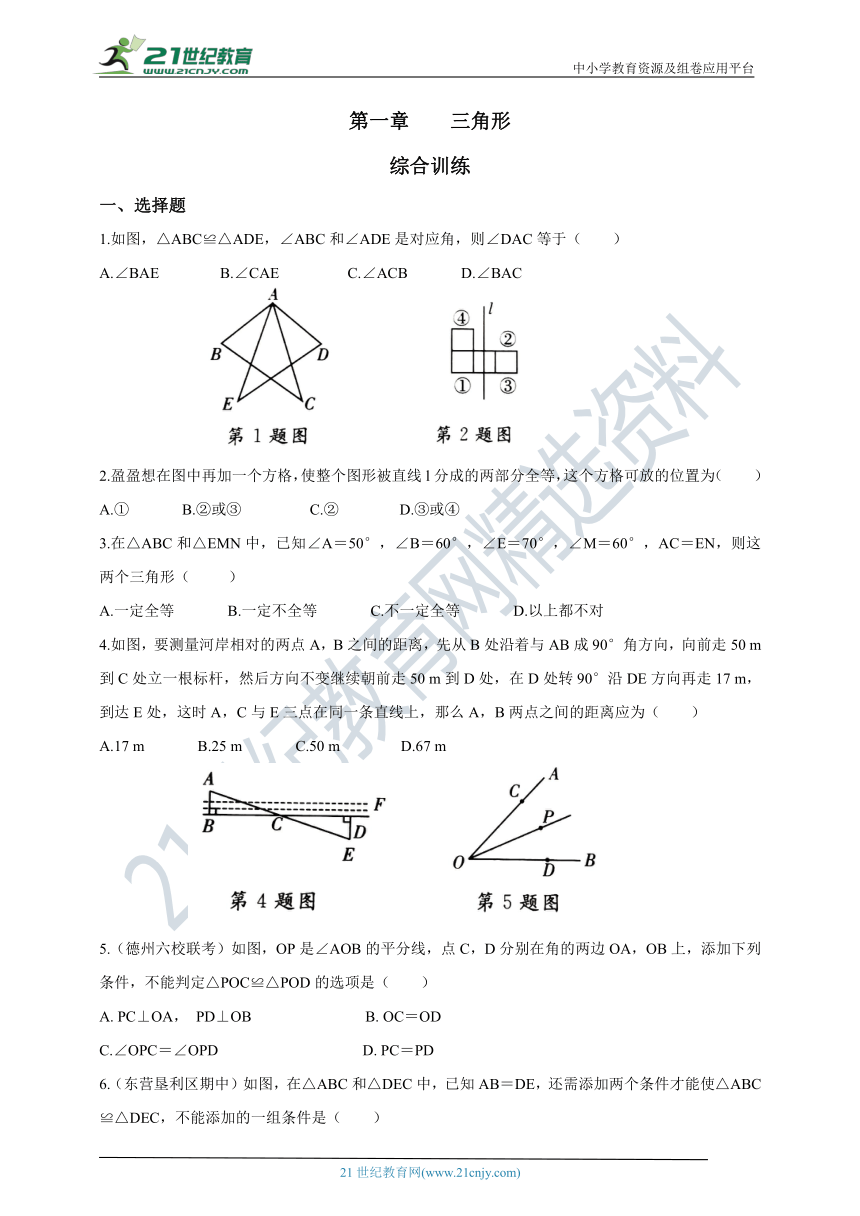
1.如图,△ABC≌△ADE,∠ABC和∠ADE是对应角,则∠DAC等于( )
A.∠BAE B.∠CAE C.∠ACB D.∠BAC
2.盈盈想在图中再加一个方格,使整个图形被直线l分成的两部分全等,这个方格可放的位置为( )A.① B.②或③ C.② D.③或④
3.在△ABC和△EMN中,已知∠A=50°,∠B=60°,∠E=70°,∠M=60°,AC=EN,则这两个三角形( )
A.一定全等 B.一定不全等 C.不一定全等 D.以上都不对
4.如图,要测量河岸相对的两点A,B之间的距离,先从B处沿着与AB成90°角方向,向前走50 m到C处立一根标杆,然后方向不变继续朝前走50 m到D处,在D处转90°沿DE方向再走17 m,到达E处,这时A,C与E三点在同一条直线上,那么A,B两点之间的距离应为( )
A.17 m B.25 m C.50 m D.67 m
5.(德州六校联考)如图,OP是∠AOB的平分线,点C,D分别在角的两边OA,OB上,添加下列条件,不能判定△POC≌△POD的选项是( )
A. PC⊥OA, PD⊥OB B. OC=OD
C.∠OPC=∠OPD D. PC=PD
6.(东营垦利区期中)如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E
B. BC=EC,AC=DCE
C.BC=DC,∠A=∠D
D.∠B=∠E,∠A=∠D
7.如图,已知∠1=∠2,∠3=∠4,则图中的全等三角形有( )
A.1对 B.2对 C.3对 D.4对
8.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D,E,AD与CE相交于点H,已知EH=EB=3,AE=4,则CH的长是( )
A.4 B.3 C.2 D.1
二、填空题
9.如图是用七巧板拼成的一艘帆船,其中全等的三角形共有__________对。
10.如图,已知∠DEF=∠B,EF=BC,现要说明△DEF≌△ABC。
若要以“SAS”为依据,还缺条件_____________________;
若要以“ASA”为依据,还缺条件_____________________;
若要以“AAS”为依据,还缺条件_____________________。
11.如图,AC与BD相交于点O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件是______________________。(填出一个即可)
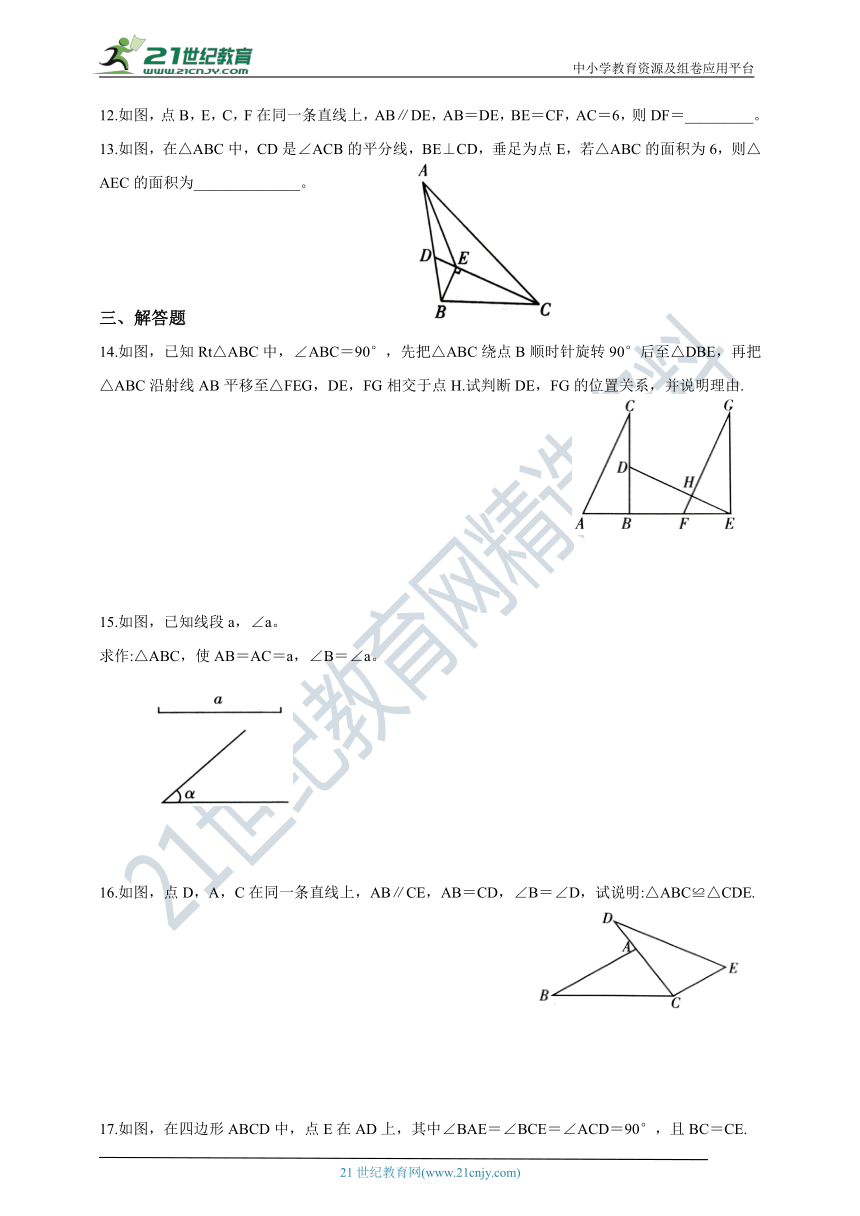
12.如图,点B,E,C,F在同一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=_________。
13.如图,在△ABC中,CD是∠ACB的平分线,BE⊥CD,垂足为点E,若△ABC的面积为6,则△AEC的面积为______________。
三、解答题
14.如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°后至△DBE,再把△ABC沿射线AB平移至△FEG,DE,FG相交于点H.试判断DE,FG的位置关系,并说明理由.
15.如图,已知线段a,∠a。
求作:△ABC,使AB=AC=a,∠B=∠a。
16.如图,点D,A,C在同一条直线上,AB∥CE,AB=CD,∠B=∠D,试说明:△ABC≌△CDE.
17.如图,在四边形ABCD中,点E在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.
试说明:△ABC与△DEC全等。
18.如图,某校学生为了测量点B到河对岸的目标A之间的距离,他们在点B同侧选择了一点C,测得∠ABC=70°,∠ACB=40°,然后在M处立了标杆,使∠MBC=70°。
(1)他们还应该怎样做才能测出A,B间的距离?
(2)画出完整的图形,说明理由.
参考答案
A 2. B
3.A 【解析】∠N=180°-60°-70°=50°,所以∠A=∠N.又因为∠B=∠M=60°,AC=EN,所以△ABC≌△NME(AAS)
4.A
5.D【解析】对于选项A,由PC⊥OA,PD⊥OB得出∠PCO=∠PDO=90°,根据“AAS”判定定理可以判定△POC≌△POD;对于选项B,OC=OD,根据“SAS”判定定理可以判定△POC≌△POD;对于选项C,∠OPC=∠OPD,根据“ASA判定定理可以判定△POC≌△POD;对于选项D,PC=PD,无法判定△POC≌△POD。
6.C
7.C【解析】由∠1=∠2,AC=AC,∠3=∠4,先得△ADC≌△ABC(ASA),进而得AD=AB,CD=CB,再利用“SAS”可得△ADE≌△ABE,△CDE≌△CBE。
8.D【解析】易证△AEH≌△CEB,所以AE=CE=4.所以CH=CE-EH=4-3=1.
9.2
10.DE=AB ∠DFE=∠ACB ∠D=∠A
11.AB=DC或OA=OD或OB=OC或∠ab=∠DCB或∠ACB=
∠DBC(答案不唯一,填一个即可)
12.6
13.3【解析】如图,延长BE交AC于点F,可证△BCE≌△FCE(ASA),所以BE=FE.则△BCE与△FCE面积相等.易知△ABE与△AFE面积相等,故△AEC的面积为△ABC面积的一半所以
S△AEC=S△ABC=3。
14.解:DE⊥FG.理由如下:
因为△DBE与△FEG是由△ABC分别经过旋转与平移得到,故有∠A=∠EDB=∠GFE,∠G=∠BED,∠ABC=∠DBE=∠GEF=90°
所以∠GFE+∠G=90°,所以∠GFE+∠BED=90°,
所以∠FHE=90°,所以DE⊥FG。
15.解:如图,(1)作∠MBN=∠a;
(2)在BN上截取AB=a,以点B为圆心,AB长为半径作弧,交射线BM于点C;
(3)连接AC,则△ABC就是所求作的三角形。
16.解:因为AB∥CE,所以∠BAC=∠DCE。
在△ABC与△CDE中,因为
所以△ABC≌△CDE(ASA)
17.解:因为∠BAE=∠BCE=∠ACD=90°,所以∠1=∠2.
因为∠3+∠4=90°,∠4+∠D=90°所以∠3=∠D。
又因为BC=CE,所以△ABC≌△DEC(AAS)。
18.解:(1)过点C作∠BCN=40°,交BM于点N,测得BN的长就是A,B间的距离.
(2)如图所示,理由如下:
因为∠ABC=70°,∠MBC=70°,∠BCN=40°,∠ACB=40°,
所以∠ABC=∠MBC,∠BCN=∠ACB
在△ABC和△NBC中,因为∠ABC=∠NBC,BC=BC,∠BCA=∠BCN,
所以△ABC≌△NBC(ASA),所以AB=BN。
_21?????????è?????(www.21cnjy.com)_
第一章 三角形
综合训练
一、选择题
1.如图,△ABC≌△ADE,∠ABC和∠ADE是对应角,则∠DAC等于( )
A.∠BAE B.∠CAE C.∠ACB D.∠BAC
2.盈盈想在图中再加一个方格,使整个图形被直线l分成的两部分全等,这个方格可放的位置为( )A.① B.②或③ C.② D.③或④
3.在△ABC和△EMN中,已知∠A=50°,∠B=60°,∠E=70°,∠M=60°,AC=EN,则这两个三角形( )
A.一定全等 B.一定不全等 C.不一定全等 D.以上都不对
4.如图,要测量河岸相对的两点A,B之间的距离,先从B处沿着与AB成90°角方向,向前走50 m到C处立一根标杆,然后方向不变继续朝前走50 m到D处,在D处转90°沿DE方向再走17 m,到达E处,这时A,C与E三点在同一条直线上,那么A,B两点之间的距离应为( )
A.17 m B.25 m C.50 m D.67 m
5.(德州六校联考)如图,OP是∠AOB的平分线,点C,D分别在角的两边OA,OB上,添加下列条件,不能判定△POC≌△POD的选项是( )
A. PC⊥OA, PD⊥OB B. OC=OD
C.∠OPC=∠OPD D. PC=PD
6.(东营垦利区期中)如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E
B. BC=EC,AC=DCE
C.BC=DC,∠A=∠D
D.∠B=∠E,∠A=∠D
7.如图,已知∠1=∠2,∠3=∠4,则图中的全等三角形有( )
A.1对 B.2对 C.3对 D.4对
8.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D,E,AD与CE相交于点H,已知EH=EB=3,AE=4,则CH的长是( )
A.4 B.3 C.2 D.1
二、填空题
9.如图是用七巧板拼成的一艘帆船,其中全等的三角形共有__________对。
10.如图,已知∠DEF=∠B,EF=BC,现要说明△DEF≌△ABC。
若要以“SAS”为依据,还缺条件_____________________;
若要以“ASA”为依据,还缺条件_____________________;
若要以“AAS”为依据,还缺条件_____________________。
11.如图,AC与BD相交于点O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件是______________________。(填出一个即可)
12.如图,点B,E,C,F在同一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=_________。
13.如图,在△ABC中,CD是∠ACB的平分线,BE⊥CD,垂足为点E,若△ABC的面积为6,则△AEC的面积为______________。
三、解答题
14.如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°后至△DBE,再把△ABC沿射线AB平移至△FEG,DE,FG相交于点H.试判断DE,FG的位置关系,并说明理由.
15.如图,已知线段a,∠a。
求作:△ABC,使AB=AC=a,∠B=∠a。
16.如图,点D,A,C在同一条直线上,AB∥CE,AB=CD,∠B=∠D,试说明:△ABC≌△CDE.
17.如图,在四边形ABCD中,点E在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.
试说明:△ABC与△DEC全等。
18.如图,某校学生为了测量点B到河对岸的目标A之间的距离,他们在点B同侧选择了一点C,测得∠ABC=70°,∠ACB=40°,然后在M处立了标杆,使∠MBC=70°。
(1)他们还应该怎样做才能测出A,B间的距离?
(2)画出完整的图形,说明理由.
参考答案
A 2. B
3.A 【解析】∠N=180°-60°-70°=50°,所以∠A=∠N.又因为∠B=∠M=60°,AC=EN,所以△ABC≌△NME(AAS)
4.A
5.D【解析】对于选项A,由PC⊥OA,PD⊥OB得出∠PCO=∠PDO=90°,根据“AAS”判定定理可以判定△POC≌△POD;对于选项B,OC=OD,根据“SAS”判定定理可以判定△POC≌△POD;对于选项C,∠OPC=∠OPD,根据“ASA判定定理可以判定△POC≌△POD;对于选项D,PC=PD,无法判定△POC≌△POD。
6.C
7.C【解析】由∠1=∠2,AC=AC,∠3=∠4,先得△ADC≌△ABC(ASA),进而得AD=AB,CD=CB,再利用“SAS”可得△ADE≌△ABE,△CDE≌△CBE。
8.D【解析】易证△AEH≌△CEB,所以AE=CE=4.所以CH=CE-EH=4-3=1.
9.2
10.DE=AB ∠DFE=∠ACB ∠D=∠A
11.AB=DC或OA=OD或OB=OC或∠ab=∠DCB或∠ACB=
∠DBC(答案不唯一,填一个即可)
12.6
13.3【解析】如图,延长BE交AC于点F,可证△BCE≌△FCE(ASA),所以BE=FE.则△BCE与△FCE面积相等.易知△ABE与△AFE面积相等,故△AEC的面积为△ABC面积的一半所以
S△AEC=S△ABC=3。
14.解:DE⊥FG.理由如下:
因为△DBE与△FEG是由△ABC分别经过旋转与平移得到,故有∠A=∠EDB=∠GFE,∠G=∠BED,∠ABC=∠DBE=∠GEF=90°
所以∠GFE+∠G=90°,所以∠GFE+∠BED=90°,
所以∠FHE=90°,所以DE⊥FG。
15.解:如图,(1)作∠MBN=∠a;
(2)在BN上截取AB=a,以点B为圆心,AB长为半径作弧,交射线BM于点C;
(3)连接AC,则△ABC就是所求作的三角形。
16.解:因为AB∥CE,所以∠BAC=∠DCE。
在△ABC与△CDE中,因为
所以△ABC≌△CDE(ASA)
17.解:因为∠BAE=∠BCE=∠ACD=90°,所以∠1=∠2.
因为∠3+∠4=90°,∠4+∠D=90°所以∠3=∠D。
又因为BC=CE,所以△ABC≌△DEC(AAS)。
18.解:(1)过点C作∠BCN=40°,交BM于点N,测得BN的长就是A,B间的距离.
(2)如图所示,理由如下:
因为∠ABC=70°,∠MBC=70°,∠BCN=40°,∠ACB=40°,
所以∠ABC=∠MBC,∠BCN=∠ACB
在△ABC和△NBC中,因为∠ABC=∠NBC,BC=BC,∠BCA=∠BCN,
所以△ABC≌△NBC(ASA),所以AB=BN。
_21?????????è?????(www.21cnjy.com)_
